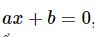Lý thuyết phương trình tích và cách giải phương trình tích kèm bài tập từ A – Z

Phương trình tích được chúng tôi sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hiệu quả hơn. Mời các bạn tham khảo.

Tham khảo thêm:

• Định nghĩa hình chóp cụt là gì? Công thức tính diện tích, thể tích hình chóp cụt kèm ví dụ có lời giải
• Quy đồng phân số là gì? Khái niệm quy đồng phân số và bài tập có lời giải chính xác 100%
• Rút gọn phân số là gì? Khái niệm rút gọn phân số và bài tập có lời giải chính xác 100%

Phương trình tích là gì?

Phương trình tích có dạng tổng quát: A( x ).B( x ) = 0

Để giải phương trình này ta áp dụng công thức:

A( x ).B( x ) = 0 ⇔ A( x ) = 0 hoặc B( x ) =0

Cách giải các phương trình đưa được về dạng phương trình tích.

Bước 1: Đưa phương trình đã cho về dạng tổng quát A( x ).B( x ) = 0 bằng cách:

   Chuyển tất cả các hạng tử của phương trình về vế trái. Khi đó vế phải bằng 0.

   Phân tích đa thức ở vế phải thành nhân tử

Bước 2: Giải phương trình và kết luận

Các dạng bài tập thường gặp ở phương trình tích

Bài tập 1: Giải các phương trình sau:

a) ( 5x – 4 )( 4x + 6 ) = 0

b) ( x – 5 )( 3 – 2x )( 3x + 4 ) = 0

Lời giải:

a) Ta có: ( 5x – 4 )( 4x + 6 ) = 0

⇒ 5x – 4 = 0 ⇔ x = 4/5; 4x + 6 = 0 ⇔ x= -3/2

b) Ta có: ( x – 5 )( 3 – 2x )( 3x + 4 ) = 0

⇒ x – 5 = 0 ⇔ x = 5; 3 – 2x = 0 ⇔ x = 2/3; 3x + 4 = 0 ⇔ x = -4/3

Bài  tập 2: Giải các phương trình sau:

a) ( 2x + 7 )² = 9( x + 2 )²

b) ( x² – 1 )( x + 2 )( x – 3 ) = ( x – 1 )( x² – 4 )( x + 5 )

c) ( 5x² – 2x + 10 )² = ( 3x² + 10x – 8 )²

d) ( x² + x )² + 4( x² + x ) – 12 = 0

Lời giải:

a) Ta có: ( 2x + 7 )² = 9( x + 2 )²

⇔ ( 2x + 7 )² – 9( x + 2 )² = 0

⇔ [ ( 2x + 7 ) + 3( x + 2 ) ][ ( 2x + 7 ) – 3( x + 2 ) ] = 0

⇔ ( 5x + 13 )( 1 – x ) = 0

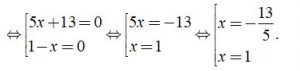
Vậy phương trình đã cho có tập nghiệm là S = { – 13/5; 1 }.

b) Ta có: ( x² – 1 )( x + 2 )( x – 3 ) = ( x – 1 )( x² – 4 )( x + 5 )

⇔ ( x² – 1 )( x + 2 )( x – 3 ) – ( x – 1 )( x² – 4 )( x + 5 ) = 0

⇔ ( x – 1 )( x + 1 )( x + 2 )( x – 3 ) – ( x – 1 )( x – 2 )( x + 2 )( x + 5 ) = 0

⇔ ( x – 1 )( x + 2 )[ ( x + 1 )( x – 3 ) – ( x – 2 )( x + 5 ) ] = 0

⇔ ( x – 1 )( x + 2 )[ ( x² – 2x – 3 ) – ( x² + 3x – 10 ) ] = 0

⇔ ( x – 1 )( x + 2 )( 7 – 5x ) = 0

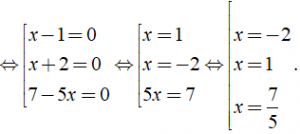
Vậy phương trình có tập nghiệm là S = { – 2; 1; 7/5 }.

c) Ta có: ( 5x² – 2x + 10 )² = ( 3x² + 10x – 8 )²

⇔ ( 5x² – 2x + 10 )² – ( 3x² + 10x – 8 )² = 0

⇔ [ ( 5x² – 2x + 10 ) – ( 3x² + 10x – 8 ) ][ ( 5x² – 2x + 10 ) + ( 3x² + 10x – 8 ) ] = 0

⇔ ( 2x² – 12x + 18 )( 8x² + 8x + 2 ) = 0

⇔ 4( x² – 6x + 9 )( 4x² + 4x + 1 ) = 0

⇔ 4( x – 3 )²( 2x + 1 )² = 0

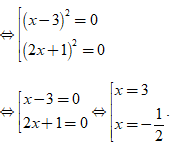
Vậy phương trình đã cho có tập nghiệm S = {- 1/2; 3}.

d) Ta có: ( x² + x )² + 4( x² + x ) – 12 = 0

Đặt t = x² + x, khi đó phương trình trở thành:

t² + 4t – 12 = 0 ⇔ ( t + 6 )( t – 2 ) = 0

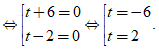
+ Với t = – 6, ta có: x² + x = – 6 ⇔ x² + x + 6 = 0 ⇔ ( x + 1/2 )² + 23/4 = 0

Mà ( x + 1/2 )² + 23/4 ≥ 23/4 ∀ x ∈ R ⇒ Phương trình đó vô nghiệm.

+ Với t = 2, ta có x² + x = 2 ⇔ x² + x – 2 = 0

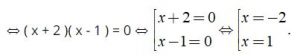
Vậy phương trình có tập nghiệm là S = { – 2;1 }.

Bài tập 3: Nghiệm của phương trình 2x(x + 1) = x² – 1

Ta có: 2x(x + 1) = x² – 1 ⇔ 2x(x + 1) = (x + 1)(x – 1)

⇔ (x + 1)(2x – x + 1) = 0 ⇔ (x + 1)(x + 1) = 0

⇔ (x + 1)² = 0 ⇔ x + 1 = 0 ⇔ x = – 1.

Vậy phương trình có nghiệm là x = – 1.

Bài tập 4: Giá trị của m để phương trình

a,(x + 2)(x – m) = 4 có nghiệm x = 2

Phương trình (x + 2)(x – m) = 4 có nghiệm x = 2, thay x = 2 vào phương trình đã cho

Khi đó ta có: (2 + 2)(2 – m) = 4 ⇔ 4(2 – m) = 4

⇔ 2 – m = 1 ⇔ m = 1.

Vậy m = 1 là giá trị cần tìm

b, Giá trị của m để phương trình x³ – x² = x + m có nghiệm x = 0

Thay x = 0 vào phương trình x³ – x² = x + m.

Khi đó ta có: 0³ – 0² = 0 + m ⇔ m = 0.

Vậy m = 0 là giá trị cần tìm.

Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình