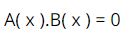Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử và bài tâp có lời giải từ A- Z

Ở bài trước các em đã biết cách phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung và dùng hằng đẳng thức. Bài này các em sẽ làm quen với một phương pháp khác để phân tích đa thức thành nhân tử đó là phương pháp nhóm hạng tử.

Tham khảo thêm:

• Đại lượng tỉ lệ nghịch là gì? Tính chất, công thức, VD có lời giải từ A – Z
• Đại lượng tỉ lệ thuận là gì? Tính chất và bài tập có lời giải từ A – Z
• Công thức tính diện tích mặt cầu và bài tập có lời giải từ A – Z

Phương pháp nhóm hạng tử

• Bước 1: Chọn và nhóm 2 hoặc 3 … hạng tử thành một nhóm sao cho mỗi nhóm sau khi phân tích thành nhân tử thì các nhóm này có thừa số chung, hoặc liên hệ các nhóm là hằng đẳng thức.
• Bước 2: Nếu các nhóm có thừa số chung. Đặt thừa số chung của các nhóm làm nhân tử chung ra ngoài ngoặc khi đó trong ngoặc là tổng các thừa số còn lại của các nhóm.

Chú ý:

• Với một đa thức, có thể có nhiều cách nhóm các hạng tử một cách thích hợp.
• Khi phân tích đa thức thành nhân tử ta phải phân tích đến cuối cùng (không còn phân tích được nữa).
• Dù phân tích bằng cách nào thì kết quả cũng là duy nhất.
• Khi nhóm các hạng tử, phải chú ý đến dấu của đa thức.

Quy tắc dấu ngoặc

• Khi bỏ dấu ngoặc có dấu “−” đứng trước, ta phải đối dấu tất cả các số hạng trong dấu ngoặc: dấu “−“ thành dấu “+” và dấu “+” thành dấu “−”.
• Khi bỏ dấu ngoặc có dấu “+” đứng trước thì dấu các số hạng trong ngoặc vẫn giữ nguyên.

Các dạng toán về phân tích đa thức bằng phương pháp nhóm hạng tử 

Dạng 1: Phân tích đa thức thành nhân tử

Phương pháp: Sử dụng cách nhóm hạng tử để phân tích đa thức thành nhân tử.

Ví dụ 1: Phân tích các đa thức sau thành nhân tử:

a, Ta có: 3x² – 3xy – 5x + 5y

= (3x² – 3xy) – (5x – 5y)

= 3x(x – y) -5(x – y) = (x – y)(3x – 5)

b, Ta có a⁴ + a³ + a³b + a²b

= (a⁴ + a³) + (a³ + a²b)

= a³(a + 1) + a²b(a + b)

= (a + 1)(a³ + a²b) = a²(a + b)(a + 1)

c, Ta có 5x² + 10xy – 4x – 8y = (5x² + 10xy) – (4x + 8y)

= 5x(x + 2y) – 4(x + 2y) = (5x – 4)(x + 2y)

d,Ta có x² + x – 2ax – 2a

= (x² + x) – (2ax + 2a) = x(x + 1) – 2a(x + 1)

= (x – 2a)(x + 1)

Ví dụ 2: Phân tích các đa thức sau thành nhân tử:

a, Ta có 2a²x – 5by – 5a²y + 2bx

= (2a²x – 5a²y) + (2bx – 5by)

= a²(2x – 5y) + b(2x – 5y)

= (a² + b)(2x – 5y)

b, Ta có x³ – 4x² – 9x + 36

= (x³ – 4x²) – (9x – 36)

= x²(x – 4) – 9(x – 4) = (x² – 9)(x – 4)

= (x – 3)(x + 3)(x – 4)

c, Ta có 2a²c² – 2abc + bd – acd = 2ac(ac – b) + d(b – ac)

= 2ac(ac – b) – d(ac – b) = (2ac – d)(ac – b)

d, Ta có ax – bx + ab – x² = (ax – x²) + (ab – bx)

= x(a – x) + b(a – x) = (x + b)(a – x)

Dạng 2: Tìm x

Phương pháp: Phân tích đa thức thành nhân tử để đưa về dạng A. B = 0 ⇒ A =0; B= 0

Ví dụ: Phân tích các đa thức sau thành nhân tử:

a, Ta có: x(x – 2) + x – 2 = 0

(x – 2)(x + 1) = 0

Hoặc x – 2 = 0 => x = 2

Hoặc x + 1 = 0 => x = -1

Vậy x = -1; x = 2

b, Ta có: x(x – 1)(x + 1) + x² – 1 = 0

⇔ x(x – 1)(x + 1) + (x² – 1) = 0

⇔ x(x – 1)(x + 1) + (x – 1)(x + 1) = 0

⇔ (x + 1)(x – 1)(x + 1) = 0

⇔ (x + 1)²(x – 1) = 0

Vậy x = -1; x= 1

Dạng 3: Tính giá trị của biểu thức thỏa mãn điều kiện cho trước.

Phương pháp: Ta biến đổi biểu thức đã cho để có thể sử dụng được điều kiện của giả thiết. Từ đó tính giá trị của biểu thức.

Chú ý: Để tính giá trị biểu thức tại x =x₀ ta thay x=x₀ vào biểu thức rồi thực hiện phép tính.

Ví dụ: Tính nhanh giá trị của mỗi đa thức: x² – 2xy – 4z² + y2 với x = 6; y = -4; z= 45

a, Ta có: x² – 2xy – 4z² + y² = (x² – 2xy + y²) – 4z²

= (x – y)² – (2z)² = (x – y + 2z)(x – y – 2z)

Thay x = 6; y = -4; z= 45 vào biểu thức ta được:

(6 + 4 + 90)(6 + 4 – 90) = 100.(-80) = -8000

b, Tính giá trị của biểu thức A = x² – 5x + xy – 5y tại x = -5; y = -8

Ta có A = x² – 5x + xy – 5y = (x² + xy) – (5x + 5y) = x(x + y) – 5(x + y)

= (x – 5)(x + y)

Tại x = -5; y = -8 ta có

A = (-5 – 5)(-5 – 8) = (-10)(-13) = 130

c, Tính giá trị của biểu thức A = (x – 1)(x – 2)(x – 3) + (x – 1)(x – 2) + x – 1 tại x = 5

Ta có A = (x – 1)(x – 2)(x – 3) + (x – 1)(x – 2) + x – 1

⇔ A = (x – 1)(x – 2)(x – 3) + (x – 1)(x – 2) + (x – 1)

⇔ A = (x – 1)[(x – 2)(x – 3) + (x – 2) + 1]

⇔ A = (x – 1)[(x – 2)(x – 3 + 1) + 1]

⇔ A = (x – 1)[(x – 2)(x – 2) + 1]

⇔ A = (x – 1)[(x – 2)² + 1]

Tại x = 5 ta có

A = (5 – 1)[(5 – 2)² + 1] = 4.(3² + 1) = 4.(9 + 1) = 4.10 = 40

Vậy A = 40

d, Tính giá trị của biểu thức B = x⁶ – 2x⁴ + x³ + x² – x khi x³ – x = 6

Ta có B = x⁶ – 2x⁴ + x³ + x² – x

⇔ B = x⁶ – x⁴ – x⁴ + x³ + x² – x

⇔ B = (x⁶ – x⁴) – (x⁴ – x²) + (x³ – x)

⇔ B = x³(x³ – x) – x(x³ – x) + (x³ – x)

⇔ B = (x³ – x + 1)(x³ – x)

Tại x³ – x = 6, ta có B = (6 + 1).6 = 7.6 = 42

Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình