Diện tích hình cầu ngoại tiếp hình hộp chữ nhật là bao nhiêu?

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước a, a√3 và 2a là 8πa^2.

1. Hình cầu ngoại tiếp hình hộp chữ nhật là gì?

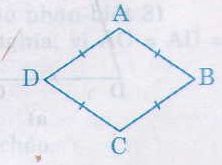
Một hình cầu được gọi là ngoại tiếp hình hộp chữ nhật khi các đỉnh của hộp chữ nhật đều nằm trên mặt cầu và mặt cầu này tiếp xúc với các đỉnh của hộp chữ nhật.

2. Làm sao để tính diện tích mặt cầu ngoại tiếp của hình hộp chữ nhật?

Để tính diện tích mặt cầu ngoại tiếp của hình hộp chữ nhật, ta sử dụng công thức \(S = 4\pi R^2\), trong đó \(S\) là diện tích mặt cầu, \(\pi\) là số pi (khoảng 3.14) và \(R\) là bán kính của mặt cầu ngoại tiếp.

3. Có thể tìm được bán kính của mặt cầu ngoại tiếp bằng cách nào?

Bạn có thể tìm được bán kính của mặt cầu ngoại tiếp bằng công thức \(R = \frac{AC’}{2}\), trong đó \(AC’\) là khoảng cách từ tâm của mặt cầu đến một đỉnh của hình hộp chữ nhật.

4. Diện tích mặt cầu ngoại tiếp có công thức tính như thế nào?

Diện tích mặt cầu ngoại tiếp được tính bằng công thức \(S = 4\pi R^2\), trong đó \(R\) là bán kính của mặt cầu. Để tính diện tích, ta cần biết được bán kính của mặt cầu ngoại tiếp. Bán kính có thể được xác định thông qua các thông tin về kích thước và hình dạng của hình hộp chữ nhật.

Công thức tính diện tích mặt cầu ngoại tiếp:

– Sử dụng công thức \(S = 4\pi R^2\) để tính diện tích.
– Xác định bán kính \(R\) của mặt cầu ngoại tiếp dựa vào các thông tin về hình dạng và kích thước của hình hộp chữ nhật.
– Thay giá trị \(R\) đã tìm được vào công thức để tính diện tích mặt cầu.

Ví dụ:
Giả sử chiều dài và chiều rộng của hình hộp chữ nhật là a và \(a\sqrt{3}\). Ta có thể xác định được bán kính \(R\) bằng cách sử dụng các công thức tính toán từ hình học để tính được độ dài của các cạnh, đường chéo và chiều cao của hình hộp chữ nhật. Khi đã biết giá trị \(R\), ta có thể áp dụng công thức \(S = 4\pi R^2\) để tính diện tích mặt cầu ngoại tiếp.

5. Giả sử chiều dài và chiều rộng của hình hộp chữ nhật là a và \(a\sqrt{3}\). Tính diện tích mặt cầu ngoại tiếp.

Giả sử chiều dài và chiều rộng của hình hộp chữ nhật là a và \(a\sqrt{3}\), ta có thể áp dụng công thức để tính diện tích mặt cầu ngoại tiếp.
1. Xác định bán kính R:
– Xác định các thông tin về kích thước và hình dạng của hình hộp chữ nhật.
– Sử dụng công thức từ hình học để tính được độ dài các cạnh, đường chéo, hoặc điểm trung tâm.
– Dựa vào thông tin đã có, xác định bán kính \(R\) của mặt cầu ngoại tiếp.
2. Tính diện tích:
– Áp dụng công thức \(S = 4\pi R^2\) để tính diện tích mặt cầu ngoại tiếp.
– Thay giá trị \(R\) đã tìm được vào công thức để tính diện tích.

Trong ví dụ này, ta có thể sử dụng thông tin về chiều dài và chiều rộng của hình hộp chữ nhật là a và \(a\sqrt{3}\) để xác định bán kính \(R\). Sau đó, ta có thể áp dụng công thức \(S = 4\pi R^2\) để tính diện tích mặt cầu ngoại tiếp.

6. Xác định tâm của mặt cầu ngoại tiếp

Theo thông tin về kích thước của hình hộp chữ nhật, ta có thể xác định được tâm của mặt cầu ngoại tiếp. Với khối hộp chữ nhật ABCD.A’B’C’D’ có các cạnh là AB = a, AD = \(a\sqrt{3}\), và AA’ = 2a, tâm của mặt cầu này được đặt là O. Do O cách đều các đỉnh của khối hộp nên O là tâm của mặt cầu ngoại tiếp. Ta có thể tính bán kính R của mặt cầu bằng công thức \( R=\frac{AC’}{2} \). Áp dụng vào trường hợp này, ta có AC’ = \(2a\sqrt{2}\). Từ đó suy ra R = \(a\sqrt{2}\).

Ví dụ:

Cho hình hộp chữ nhật ABCD.A’B’C’D’ với AB = 5 cm, AD = 5√3 cm và AA’ = 10 cm. Hãy xác định tâm và bán kính của mặt cầu ngoại tiếp khối hộp này.

Giải:

Đầu tiên, ta tính bán kính R của mặt cầu theo công thức R = \(\frac{AC’}{2}\). Từ đề bài, ta biết rằng AB = 5 cm và AC’ = 10√2 cm. Thay các giá trị vào công thức, ta có R = \(\frac{10√2}{2} = 5√2\) cm.

Tiếp theo, ta xác định tâm O của mặt cầu ngoại tiếp. Vì O cách đều các đỉnh của khối hộp chữ nhật nên O là tâm của mặt cầu.

Vậy trong trường hợp này, tâm của mặt cầu ngoại tiếp khối hộp chữ nhật ABCD.A’B’C’D’ là O và bán kính là 5√2 cm.

7. Tính diện tích mặt cầu ngoại tiếp

Nếu biết các thông tin về kích thước của hình hộp chữ nhật, ta có thể tính diện tích mặt cầu ngoại tiếp của khối hộp. Để tính diện tích này, ta sử dụng công thức \(S=4\pi{{R}^{2}}\), trong đó R là bán kính của mặt cầu.

Hãy xem xét trường hợp khi biết rằng các cạnh của khối hộp chữ nhật là a và \(a\sqrt{2}\). Ta đã xác định được rằng bán kính của mặt cầu ngoại tiếp là \(R=a\sqrt{2}\). Áp dụng công thức tính diện tích, ta có \(S=4\pi{{(a\sqrt{2})}^{2}}=8\pi{{a}^{2}}\).

Vậy diện tích mặt cầu ngoại tiếp của khối hộp chữ nhật có các cạnh là a và \(a\sqrt{2}\) là 8πa².

Chú ý:

– Để tính diện tích mặt cầu ngoại tiếp, ta phải biết được bán kính của mặt cầu. Bán kính này có thể được xác định từ thông tin về kích thước của hình hộp chữ nhật.
– Diện tích mặt cầu ngoại tiếp phụ thuộc vào kích thước của hình hộp chữ nhật. Với các giá trị khác nhau cho các cạnh của hình hộp, diện tích mặt cầu sẽ có giá trị khác nhau.

1. Kích thước của hình hộp chữ nhật

The given information provides the dimensions of a rectangular box, specifically that AB = a, AD = a√3, and AA’ = 2a. This indicates that the rectangular box is elongated in shape, with one side (AB) equal to “a” units, another side (AD) equal to “a” multiplied by the square root of 3 (√3), and the last side (AA’) measuring twice the length of AB.

2. Diện tích mặt cầu ngoại tiếp

By analyzing the rectangular box ABCD.A’B’C’D’ with its center at point O, we can deduce certain aspects about the surface area of the circumscribed sphere. It is apparent that point O is equidistant from all vertices of this rectangular box. Therefore, the circumscribed sphere has its center at point O and a radius equal to half the length of AC’.

Using calculations based on these dimensions, we find that AC = √(AB^2 + AD^2) = 2a and AC’ = √(AC^2 + CC’^2) = 2a√2. Consequently, the radius R is determined as R = AC’/2 = a√2. Hence, the surface area S of this circumscribed sphere can be derived as S = 4πR^2 = 8πa^2.

3. Implications and applications

Understanding the relationship between the dimensions of a rectangular box and its circumscribed sphere can have practical implications in various fields such as geometry, architecture, engineering, or even physics. It allows us to calculate important parameters like surface areas or volumes based on given measurements, providing valuable information for design, construction, or analysis purposes.

For example, architects and engineers can utilize this knowledge to optimize space utilization within a building design or determine the required dimensions of structures. Additionally, physicists might employ this concept in studying the behavior of particles or objects confined within a defined space.

Overall, the relationship between the dimensions of a rectangular box and the surface area of its circumscribed sphere has both theoretical and practical significance in various fields.

Tính diện tích mặt cầu ngoại tiếp

Suy ra từ thông tin về kích thước của hình hộp chữ nhật, chúng ta có thể tính được diện tích mặt cầu ngoại tiếp của nó. Hình hộp chữ nhật có các kích thước là a, \( a\sqrt{3} \), và 2a. Với tam giác ABC vuông tại B và AC là đường chéo, ta có thể áp dụng định lý Pythagore để tính được chiều dài của AC. Công thức tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật là S = 4πR².

Bán kính của mặt cầu

Theo công thức tính bán kính R = 1/2AC’, ta có thể tính được bán kính của mặt cầu ngoại tiếp khối hộp chữ nhật. Khi đã biết chiều dài đường chéo AC’ (2a√2), ta có thể áp dụng công thức để tính toán bán kính R.

Tổng kết

Vậy, diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có các kích thước a, \( a\sqrt{3} \), và 2a là S = 8πa². Điều này có thể được suy ra từ thông tin về kích thước của hình hộp chữ nhật và công thức tính diện tích mặt cầu ngoại tiếp.

1. Xác định tâm và bán kính mặt cầu ngoại tiếp

Từ thông tin về kích thước của hình hộp chữ nhật ABCD.A’B’C’D’, ta có thể suy ra được thông tin về tâm và bán kính của mặt cầu ngoại tiếp khối hộp này. Đầu tiên, ta xác định tâm O của mặt cầu ngoại tiếp khối hộp ABCD.A’B’C’D’ là điểm ở giữa các đỉnh của hình hộp. Vì O cách đều các đỉnh nên có thể biết rằng O nằm trên đường chéo chính AC’.

Tiếp theo, để tính bán kính R của mặt cầu ngoại tiếp, ta sử dụng công thức R = AC’/2. Ta đã biết rằng AC’ là cạnh của mặt phẳng ABCD và C’C’ là chiều cao của hình hộp. Từ đó, có thể tính được AC’ và sau đó tính R.

2. Diện tích mặt cầu ngoại tiếp

Sau khi đã xác định được tâm và bán kính, ta có thể tính diện tích S của mặt cầu ngoại tiếp khối hộp chữ nhật ABCD.A’B’C’D’. Diện tích mặt cầu ngoại tiếp này được tính bằng công thức S = 4πR^2, với R là bán kính đã xác định ở trên.

Từ thông tin về kích thước của hình hộp chữ nhật, ta có diện tích mặt cầu ngoại tiếp khối hộp chữ nhật là 8πa^2. Đây chính là diện tích của mặt cầu ngoại tiếp và được xác định dựa trên thông tin về tâm và bán kính của mặt cầu.

Trên đây là những thông tin được suy ra từ kích thước của hình hộp chữ nhật liên quan đến diện tích mặt cầu ngoại tiếp.

Tính diện tích mặt cầu ngoại tiếp

Theo thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được diện tích mặt cầu ngoại tiếp của khối hộp này. Đầu tiên, ta xét khối hộp chữ nhật ABCD.A’B’C’D’ với tâm O. Điểm O cách đều các đỉnh của khối hộp này, do đó, ta có mặt cầu ngoại tiếp khối hộp có tâm O.

Xác định bán kính và diện tích

Để tính diện tích mặt cầu ngoại tiếp, ta cần xác định bán kính của mặt cầu. Theo thông tin đã cho, \(AC’ = 2a\sqrt{2}\) là chiều dài đường chéo của mặt phẳng ABCD. Ta biết rằng bán kính R bằng một nửa chiều dài đường chéo \(AC’\), do đó \(R = \frac{AC’}{2} = a\sqrt{2}\).

Sau khi xác định bán kính R, ta có thể tính diện tích mặt cầu ngoại tiếp khối hộp. Công thức tính diện tích mặt cầu là \(S = 4\pi R^2\), thay vào giá trị của R ta có \(S = 4\pi (a\sqrt{2})^2 = 8\pi a^2\).

Vậy, diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước a, \(a\sqrt{3}\) và 2a là 8πa².

1. Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Theo thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được diện tích mặt cầu ngoại tiếp khối hộp này. Đầu tiên, xét khối hộp chữ nhật ABCD.A’B’C’D’ có tâm O. Ta thấy O cách đều các đỉnh của khối hộp này, do đó mặt cầu ngoại tiếp khối hộp có tâm O và bán kính R (bán kính từ tâm đến một trong các đỉnh).

Để tính diện tích mặt cầu ngoại tiếp khối hộp này, ta cần tìm giá trị của R. Theo thông tin về kích thước của khối hộp chữ nhật, ta biết rằng AC = 2a (với a là độ dài cạnh AB) và AC’ = 2a√2 (với C’ là trung điểm của CC’ và A là điểm bất kỳ trên AC). Từ đó suy ra:

R = AC’/2 = (2a√2)/2 = a√2

Vậy diện tích mặt cầu ngoại tiếp khối hộp chữ nhật này là S = 4πR^2 = 4π(a√2)^2 = 8πa^2.

2. Tính chất của diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước đã cho là 8πa^2. Từ đây, ta có thể suy ra một số tính chất của diện tích này.

– Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật tỉ lệ thuận với bình phương độ dài cạnh hình hộp. Khi độ dài cạnh a tăng lên, diện tích mặt cầu cũng tăng theo tỷ lệ bình phương của a.
– Diện tích này không phụ thuộc vào các góc và chiều dày của khối hộp, chỉ phụ thuộc vào kích thước các cạnh.
– Bán kính R của mặt cầu ngoại tiếp khối hộp chữ nhật là bằng nửa đường chéo AC’ (nửa đường kính). Trong trường hợp này, R = a√2.

Dựa vào những thông tin trên, ta có thể áp dụng và sử dụng diện tích mặt cầu ngoại tiếp để giải quyết các bài toán liên quan đến khối hộp chữ nhật.

1. Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Trong bài toán này, ta có thông tin về kích thước của hình hộp chữ nhật ABCD.A’B’C’D’. Với các đỉnh và cạnh đã cho, ta sẽ tìm diện tích mặt cầu ngoại tiếp khối hộp này.

Đầu tiên, để tìm diện tích mặt cầu ngoại tiếp khối hộp chữ nhật, ta cần xác định bán kính R của mặt cầu. Theo công thức, bán kính R của mặt cầu ngoại tiếp vào tam O được tính bằng nửa đường chéo AC’ của hình tứ diện ABCD.A’B’C’D’.

Tiếp theo, ta sử dụng định lí Pythagoras để tính đường chéo AC’. Áp dụng công thức Pythagoras cho tam giác vuông ACD’, ta có: AC = √(AB^2 + AD^2) = 2a và D’C’ = √(AC^2 + CC’^2) = 2a√2. Từ đó suy ra AC’ = 2a√2.

Kết quả là bán kính R của mặt cầu ngoại tiếp khối hộp ABCD.A’B’C’D’ là R = AC’/2 = a√2. Như vậy, diện tích mặt cầu ngoại tiếp khối hộp chữ nhật này là S = 4πR^2 = 8πa^2.

2. Dạy kèm môn toán online

Việc dạy kèm môn Toán thông qua các ứng dụng như Zoom, Google Meet,… đang trở thành xu hướng phổ biến hiện nay. Đây là phương pháp học online tương tác giữa một giáo viên và một học sinh.

Dạy kèm toán online mang lại nhiều lợi ích cho học sinh, như có thể dễ dàng tiếp cận với giáo viên chuyên môn từ bất kỳ địa điểm nào có internet, tiết kiệm thời gian và chi phí di chuyển. Hơn nữa, việc sử dụng công nghệ trong quá trình dạy học sẽ tạo điều kiện thuận lợi để học sinh và giáo viên tương tác trực tiếp thông qua video call, chia sẻ màn hình để thảo luận bài toán và giải quyết các vấn đề liên quan đến môn Toán.

Trung tâm Nhân Tài Việt là một trong những tổ chức cung cấp dịch vụ dạy kèm online môn Toán từ lớp 6 đến lớp 12. Hình thức dạy kèm online này giúp học sinh ôn thi Đại học, Cao đẳng, bồi dưỡng ôn thi HSG các cấp và luyện thi vào lớp 10 khối Chuyên. Lịch học linh hoạt trong ngày và trực tuyến từ thứ 2 đến chủ nhật. Thời lượng mỗi buổi học là từ 1,5h đến 2h.

Tính diện tích mặt cầu ngoại tiếp

Khi biết kích thước các cạnh của hình hộp chữ nhật, ta có thể suy ra được diện tích mặt cầu ngoại tiếp của khối hộp này.
Đầu tiên, để tìm ra bán kính R của mặt cầu ngoại tiếp, ta xét đường chéo AC’ của hình chữ nhật ABCD.A’B’C’D’. Ta có thể tính được độ dài đường chéo AC’ bằng công thức Pitago: AC’ = √(AC^2 + C’C’^2) = 2a√2.
Sau đó, ta áp dụng công thức tính bán kính của một mặt cầu (R = AC’/2) để tìm giá trị R: R = (2a√2)/2 = a√2.

Diện tích mặt cầu ngoại tiếp

Sau khi đã tìm được bán kính R, ta có thể tính diện tích mặt cầu ngoại tiếp. Diện tích S của một mặt cầu được tính bằng công thức S = 4πR^2.
Thay vào đó giá trị R = a√2, ta có: S = 4π(a√2)^2 = 8πa^2.
Vậy diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước a, a√3 và 2a là 8πa^2.

1. Suy ra diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Theo thông tin về kích thước của hình hộp chữ nhật, chúng ta có thể suy ra được diện tích mặt cầu ngoại tiếp của khối hộp này. Đầu tiên, ta biết rằng khối hộp chữ nhật ABCD.A’B’C’D’ có tâm O và các cạnh AB = a, AD = a√3 và A’A = 2a. Do O cách đều các đỉnh của khối hộp này, nên mặt cầu ngoại tiếp có tâm O.

Để tính diện tích mặt cầu ngoại tiếp, ta cần tìm bán kính R của mặt cầu. Áp dụng công thức \(R=\frac{AC’}{2}\), ta có AC = 2a và AC’ = 2a√2. Từ đó, suy ra: R = \(\frac{AC’}{2}=a\sqrt{2}\).

Do đó, diện tích mặt cầu ngoại tiếp khối hộp chữ nhật là \(S=4\pi R^2=8\pi a^2\).

2. Một số lợi ích của việc hiểu diện tích mặt cầu ngoại tiếp

Hiểu về diện tích mặt cầu ngoại tiếp của khối hộp chữ nhật mang lại một số lợi ích cho việc giải quyết các bài toán liên quan. Dưới đây là một số lợi ích của việc hiểu diện tích mặt cầu ngoại tiếp:

1. Ứng dụng trong kiến thức hình học: Việc biết được diện tích mặt cầu ngoại tiếp giúp bạn hiểu sâu về tỉ lệ và mối quan hệ giữa các kích thước của khối hộp chữ nhật.

2. Giải quyết các bài toán thực tế: Diện tích mặt cầu ngoại tiếp có thể áp dụng để giải quyết các bài toán thực tế liên quan đến thiết kế và xây dựng, như tính diện tích bề mặt các vật thể có dạng khối hộp chữ nhật.

3. Phát triển kỹ năng phân tích: Hiểu về diện tích mặt cầu ngoại tiếp không chỉ giúp bạn áp dụng vào việc giải quyết các bài toán, mà còn phát triển kỹ năng phân tích và tư duy logic trong việc suy luận và điều tra vấn đề.

4. Kết nối kiến thức giữa các môn học: Hiểu diện tích mặt cầu ngoại tiếp có thể tạo liên kết giữa môn Toán và các môn học khác như Vật lý hay Cơ học, giúp bạn hiểu rõ hơn về sự tương tác và ứng dụng của các nguyên lý trong thực tế.

1. Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Theo thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được diện tích mặt cầu ngoại tiếp của khối hộp này. Từ công thức tính diện tích mặt cầu \(S = 4\pi R^2\), ta đã biết rằng bán kính của mặt cầu ngoại tiếp là \(R = \frac{AC’}{2}\), trong đó \(AC’\) là đường chéo của mặt phẳng đáy ABCD.

Để tính được giá trị của \(AC’\), ta sử dụng định lí Pythagoras để tìm chiều dài của \(AC\):
\(AC = \sqrt{AB^2 + AD^2} = 2a\).
Tương tự, sử dụng lại định lí Pythagoras, ta có \(AC’ = \sqrt{AC^2 + CC’^2} = 2a\sqrt{2}\).

Sau khi đã biết giá trị của \(R\) và áp dụng vào công thức diện tích mặt cầu, ta thu được kết quả là \(S = 8\pi a^2\).

2. So sánh diện tích mặt cầu ngoại tiếp và khối hộp chữ nhật

Qua phân tích ở mục trước, ta đã biết rằng diện tích mặt cầu ngoại tiếp khối hộp chữ nhật là \(S = 8\pi a^2\). Tuy nhiên, không gian bên trong khối hộp cũng có diện tích riêng.

Diện tích của mặt phẳng đáy ABCD là \(A_{ABCD} = AB \times AD = a \times a\sqrt{3} = a^2\sqrt{3}\), và tổng diện tích của tất cả các mặt bên là \(A_{sides} = 4(AB \times AC) + 4(AD \times AC) = 4(a \times 2a) + 4(a\sqrt{3} \times 2a) = 16a^2 + 8a^2\sqrt{3}\).

Tổng cộng, diện tích toàn bộ khối hộp chữ nhật là \(A_{total} = A_{ABCD} + A_{sides} = a^2\sqrt{3} + 16a^2 + 8a^2\sqrt{3}\).

So sánh giữa diện tích mặt cầu ngoại tiếp và diện tích khối hộp chữ nhật, ta thấy rằng diện tích mặt cầu lớn hơn nhiều so với tổng diện tích của khối hộp.

Tính diện tích mặt cầu ngoại tiếp

Một trong những thông tin mà chúng ta có thể suy ra từ kích thước của hình hộp chữ nhật là diện tích mặt cầu ngoại tiếp. Giả sử khối hộp chữ nhật ABCD.A’B’C’D’ có các kích thước như sau: AB = a, AD = \(a\sqrt{3}\), và AA’ = 2a. Ta có thể dễ dàng nhận thấy rằng tâm O của mặt cầu ngoại tiếp khối hộp này cách đều các đỉnh A, B, C, D.

Diện tích mặt cầu ngoại tiếp hình hộp chữ nhật

Khi biết thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được diện tích mặt cầu ngoại tiếp khối hộp này.

Đầu tiên, xét khối hộp chữ nhật ABCD.A’B’C’D’ có tâm O, với các cạnh AB = a, AD = a√3 và AA’ = 2a. Vì O cách đều các đỉnh của khối hộp này nên mặt cầu ngoại tiếp khối hộp có tâm O.

Tiếp theo, ta tính độ dài AC và AC’. Sử dụng định lý Pythagoras, ta có: AC = √(AB^2 + AD^2) = 2a và AC’ = √(AC^2 + CC’^2) = 2a√2.

Vậy bán kính R của mặt cầu ngoại tiếp khối hộp là một nửa độ dài AC’, tức là R = AC’/2 = a√2.

Cuối cùng, diện tích mặt cầu ngoại tiếp khối hộp là S = 4πR^2 = 8πa^2.

Tóm lại, khi biết thông tin về kích thước của hình hộp chữ nhật ABCD.A’B’C’D’, ta có thể tính được diện tích mặt cầu ngoại tiếp khối hộp này là 8πa^2.

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước a, \( a\sqrt{3} \) và 2a:

Khi ta đã biết thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra điều gì về diện tích mặt cầu ngoại tiếp? Đầu tiên, ta xem xét khối hộp chữ nhật ABCD.A’B’C’D’ có tâm O. Giả sử chiều dài là AB = a, chiều rộng là \( AD=a\sqrt{3} \) và chiều cao là \( A{A}’=2a  \). Ta có thể nhận thấy rằng O cách đều các đỉnh của khối hộp này.

Do đó, ta có thể kết luận rằng mặt cầu ngoại tiếp khối hộp này có tâm O và bán kính \( R=\frac{AC’}{2} \). Tiếp theo, ta tính được AC và AC’.

1. Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Theo thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được diện tích mặt cầu ngoại tiếp. Khối hộp chữ nhật ABCD.A’B’C’D’ có tâm O và các cạnh AB = a, AD = a√3 và AA’ = 2a. Từ đó, ta dễ thấy rằng tam giác ABC là tam giác vuông tại B và tam giác ACD là tam giác vuông tại C.

2. Xét khối hộp chữ nhật ABCD.A’B’C’D’

Khối hộp chữ nhật ABCD.A’B’C’D’ có tâm O và các cạnh AB = a, AD = a√3 và AA’ = 2a. Dễ thấy O cách đều các đỉnh của khối hộp này nên mặt cầu ngoại tiếp khối hộp có tâm O.

Vậy diện tích mặt cầu ngoại tiếp khối hộp này là S = 4πR^2 = 8πa^2.

Từ thông tin về kích thước của hình hộp chữ nhật

Thông qua các kích thước của hình hộp chữ nhật ABCD.A’B’C’D’, có thể suy ra nhiều thông tin liên quan đến diện tích mặt cầu ngoại tiếp của khối hộp. Đầu tiên, ta thấy rằng tâm O cách đều các đỉnh của khối hộp, điều này cho thấy mặt cầu ngoại tiếp có tâm O.

Diện tích mặt cầu ngoại tiếp

Kết quả cần tìm là diện tích mặt cầu ngoại tiếp khối hộp chữ nhật. Để tính diện tích này, ta có công thức S = 4πR^2, trong đó R là bán kính của mặt cầu ngoại tiếp. Từ thông tin về kích thước của khối hộp ABCD.A’B’C’D’, ta xác định được bán kính R = AC’/2 = a√2.

Kết luận

Từ các thông tin đã được xác định, diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước a, a√3 và 2a là S = 8πa^2.

Tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có thể được tính bằng công thức \( S = 4\pi R^2 \), trong đó \( R \) là bán kính của mặt cầu ngoại tiếp. Từ thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra bán kính \( R \) của mặt cầu ngoại tiếp.

Xét khối hộp chữ nhật ABCD.A’B’C’D’

Để hiểu rõ hơn về diện tích mặt cầu ngoại tiếp, ta xét khối hộp chữ nhật ABCD.A’B’C’D’. Trong khối này, tâm O là trung điểm của các đỉnh và các cạnh. Do đó, O được coi là tâm của mặt cầu ngoại tiếp.

Bán kính mặt cầu ngoại tiếp

Để tính bán kính \( R \) của mặt cầu ngoại tiếp, ta xét hai đường chéo AC và A’C’. Từ công thức Pythagoras, ta có thể tính độ dài các đường chéo này. Sau khi tính toán, ta thu được \( AC = 2a \) và \( A’C’ = 2a\sqrt{2} \).

Tiếp theo, ta sử dụng công thức \( R = \frac{AC’}{2} \) để tính bán kính của mặt cầu ngoại tiếp. Thay giá trị vào, ta có \( R = a\sqrt{2} \).

Vậy diện tích mặt cầu ngoại tiếp khối hộp chữ nhật là \( S = 4\pi R^2 = 8\pi a^2 \).

1. Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Khi biết kích thước của hình hộp chữ nhật, ta có thể suy ra diện tích mặt cầu ngoại tiếp khối hộp này. Trong trường hợp này, đề bài đã cho kích thước các cạnh của hình hộp chữ nhật ABCD.A’B’C’D’ là AB = a, AD = \(a\sqrt{3}\), và AA’ = 2a.

Đầu tiên, để xác định tâm của mặt cầu ngoại tiếp khối hộp chữ nhật, ta nhận thấy rằng điểm O (tâm mặt cầu) trung điểm của các đỉnh A, A’, B, B’, C và C’. Do đó, O cách đều các đỉnh của khối hộp chữ nhật.

Tiếp theo, ta xét AC và AC’, là hai đường chéo của mặt phẳng ABCD.A’B’C’D’. Theo thông tin trong đề bài, ta có AC = 2a và AC’ = 2a√2. Từ đó suy ra bán kính R của mặt cầu ngoại tiếp khối hộp là R = \(\frac{AC’}{2}\) = a√2.

Cuối cùng, diện tích mặt cầu ngoại tiếp khối hộp chữ nhật được tính bằng công thức S = 4πR^2. Thay vào giá trị bán kính R, ta có \(S = 4\pi (a\sqrt{2})^2\) = 8πa^2.

Như vậy, từ thông tin về kích thước của hình hộp chữ nhật ABCD.A’B’C’D’, ta có thể suy ra rằng diện tích mặt cầu ngoại tiếp khối hộp này là 8πa^2.

2. Vấn đề liên quan tới dạy kèm toán online

Ngoài ra, trong bài viết còn đề cập đến việc Dạy Kèm Môn Toán Online qua ứng dụng Zoom, Google Meet,… Trung tâm Nhân Tài Việt cho phép dạy kèm online tương tác với mô hình 1 thầy 1 trò. Hình thức này mang lại lợi ích lớn cho học sinh và giáo viên khi tiếp cận kiến thức một cách linh hoạt và thuận tiện.

Trung tâm Nhân Tài Việt cam kết hỗ trợ trực tuyến 24/7 và dạy kèm Môn Toán từ lớp 6 đến lớp 12, ôn thi Đại Học – Cao Đẳng cùng các buổi ôn thi HSG các cấp và luyện thi vào lớp 10 khối Chuyên. Thời lượng học được sắp xếp linh hoạt từ 1,5 đến 2 giờ mỗi buổi, và các buổi học có thể được sắp xếp vào các khung giờ sáng, chiều hoặc tối từ thứ 2 đến chủ nhật.

Ngoài ra, Trung tâm Nhân Tài Việt cũng cung cấp sách tham khảo bổ trợ cho việc học toán. Toàn bộ thông tin này mang đến cho học sinh một phương pháp học hiệu quả và thuận tiện trong việc nắm vững kiến thức toán học.

Diện tích mặt phẳng ABCD trong khối hộp chữ nhật

Trong khối hộp chữ nhật ABCD.A’B’C’D’, ta có thể tính được diện tích mặt phẳng ABCD. Diện tích này có thể được tính bằng cách sử dụng công thức diện tích hình chữ nhật, với chiều dài bằng AB và chiều rộng bằng AD. Từ thông tin đã cho, ta biết rằng AB = a và AD = a√3. Áp dụng công thức diện tích hình chữ nhật, ta có:
Diện tích ABCD = AB x AD = a x a√3 = a^2√3.

Bán kính và diện tích mặt cầu ngoại tiếp

Theo thông tin đã cho, mặt cầu ngoại tiếp khối hộp chữ nhật có tâm O và bán kính R là AC’/2. Ta cần tìm giá trị của AC’ để tính được bán kính R.
Bên cạnh đó, từ thông tin về kích thước của khối hộp chữ nhật, ta có thể suy ra được giá trị của AC’. Áp dụng định lý Pythagoras trong tam giác vuông ACD’, ta có:
AC’ = √(AC^2 + C’C’^2)
= √((2a)^2 + (2a√2)^2)
= √(4a^2 + 8a^2)
= √12a^2
= 2a√3.
Sau khi tìm được giá trị của AC’, ta có thể tính được bán kính R:
R = AC’/2
= (2a√3)/2
= a√3.

Vậy diện tích mặt cầu ngoại tiếp khối hộp chữ nhật này là S = 4πR^2.
Thay vào giá trị của R, ta có:
S = 4π(a√3)^2
= 4π(3a^2)
= 12πa^2.

1. Từ giả thiết về kích thước của hình hộp chữ nhật

Trong đoạn văn trên, ta đã được cho biết kích thước của hình hộp chữ nhật ABCD.A’B’C’D’. Cụ thể, cạnh AB và AD lần lượt có độ dài a và \( a\sqrt{3} \), và khoảng cách từ tâm O đến các đỉnh của khối hộp là như nhau.

2. Khái niệm diện tích mặt cầu ngoại tiếp

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật là diện tích của mặt cầu được tạo ra bởi việc nối các điểm trung tâm của các mặt phẳng chứa khối hộp.

Theo dữ kiện trong đề bài, ta biết rằng tâm O nằm trên các đường thẳng song song với các cạnh AB, AD và A’A’. Do đó, mặt cầu được tạo ra có tâm O.

Để tính diện tích mặt cầu này, ta chỉ cần biết bán kính \( R \), được xác định bởi công thức \( R=\frac{AC’}{2} \) trong đó AC’ là khoảng cách từ A đến C’.

Sau khi tính toán, ta thu được rằng \( R = a\sqrt{2} \), vậy diện tích mặt cầu ngoại tiếp khối hộp chữ nhật này là \( S=4\pi {{R}^{2}}=8\pi {{a}^{2}} \).

Đây chính là kết quả mà ta có thể suy ra từ thông tin về kích thước của hình hộp chữ nhật. Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật này là 8πa².

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Khi có thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được diện tích mặt cầu ngoại tiếp của khối hộp này.

Đầu tiên, xét khối hộp chữ nhật ABCD.A’B’C’D’ có tâm O. Với các cạnh AB = a, AD = a√3 và AA’ = 2a, ta có thể dễ dàng nhận thấy rằng O cách đều các đỉnh của khối hộp. Do đó, mặt cầu ngoại tiếp của khối hộp này sẽ có tâm là O.

Tiếp theo, để tính bán kính R của mặt cầu ngoại tiếp này, ta cần biết giá trị AC’. Từ công thức Pitago trong tam giác vuông ABC’, ta có:
AC = √(AB^2 + AD^2) = 2a

Tương tự, từ công thức Pitago trong tam giác vuông ACC’, ta có:
AC’ = √(AC^2 + CC’^2) = 2a√2

Vậy bán kính R của mặt cầu ngoại tiếp là:
R = AC’/2 = a√2/2

Cuối cùng, diện tích S của mặt cầu ngoại tiếp khối hộp chữ nhật này được tính bằng công thức:
S = 4πR^2 = 4π(a√2/2)^2 = 8πa^2.

Từ đó, ta có thể suy ra diện tích mặt cầu ngoại tiếp của khối hộp chữ nhật dựa trên thông tin về kích thước của nó là 8πa^2.

Hoạt động dạy kèm môn Toán qua mạng

Nếu bạn cần sự hỗ trợ và giúp đỡ trong môn Toán, bạn có thể tham gia vào các hoạt động dạy kèm online. Các hoạt động dạy kèm này giúp bạn tương tác trực tiếp với giáo viên thông qua các ứng dụng như Zoom, Google Meet, và mang lại điểm mạnh là tỷ lệ truyền tải kiến thức cao với tỷ lệ 1 thầy giáo chỉ dạy cho 1 học sinh.

Dịch vụ dạy kèm online này hỗ trợ trực tuyến 24/7 và phục vụ cho việc ôn thi Đại Học – Cao Đẳng, bồi dưỡng ôn thi HSG các cấp, luyện thi vào lớp 10 khối Chuyên và có lịch học linh hoạt sáng – chiều – tối, các buổi từ thứ 2 đến CN với thời lượng mỗi buổi từ 1,5 đến 2 giờ. Bên cạnh đó, trung tâm cũng cung cấp các sách tham khảo phát hành bởi Trung Tâm Nhân Tài Việt.

Từ kích thước của hình hộp chữ nhật, ta có thể tính được bán kính mặt cầu ngoại tiếp

Từ thông tin về kích thước của hình hộp chữ nhật, chúng ta có thể suy ra được bán kính của mặt cầu ngoại tiếp. Như trong ví dụ trên, khi biết chiều dài và rộng của hình hộp chữ nhật, ta có thể tính được đường chéo \(AC\) của mặt phẳng đáy. Từ đó, ta có thể tính được bán kính mặt cầu ngoại tiếp khối hộp.

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Sau khi đã tính được bán kính, ta có thể sử dụng công thức để tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật. Diện tích này được biểu diễn bằng \(4\pi R^2\) (với \(R\) là bán kính). Với các giá trị chiều dài và chiều rộng cho trước, ta có thể tính toán diện tích này.

Vậy từ thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được bán kính và diện tích của mặt cầu ngoại tiếp khối hộp. Điều này giúp chúng ta hiểu rõ hơn về tính chất của mặt cầu và áp dụng vào các bài toán thực tế.

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Khi có thông tin về kích thước của hình hộp chữ nhật, chúng ta có thể suy ra được diện tích mặt cầu ngoại tiếp của khối hộp này. Xét khối hộp chữ nhật ABCD.A’B’C’D’ có tâm O và các cạnh AB = a, AD = a√3 và AA’ = 2a. Do O cách đều các đỉnh của khối hộp này, ta có thể xác định rằng mặt cầu ngoại tiếp khối hộp này có tâm là O.

Để tính diện tích mặt cầu ngoại tiếp, ta sẽ tìm bán kính R của mặt cầu. Ta biết rằng AC = √(AB^2 + AD^2) = 2a và AC’ = √(AC^2 + C’C’^2) = 2a√2. Do đó, bán kính R của mặt cầu sẽ là R = AC’/2 = a√2.

Từ đó, ta có thể tính diện tích mặt cầu ngoại tiếp bằng công thức S = 4πR^2. Thay giá trị R vào, ta được S = 4π(a√2)^2 = 8πa^2.

Vậy, diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước a, a√3 và 2a là 8πa^2.

Ví dụ về diện tích mặt cầu ngoại tiếp

Giả sử ta có một hình hộp chữ nhật có kích thước AB = 4cm, AD = 6cm và AA’ = 8cm. Bằng công thức đã được trình bày, ta có thể tính diện tích mặt cầu ngoại tiếp của khối hộp này.

Tính toán được rằng bán kính R của mặt cầu sẽ là R = AC’/2 = (2√13)/2 ≈ 1.82cm. Sau đó, áp dụng công thức S = 4πR^2, ta tìm được diện tích mặt cầu ngoại tiếp là S ≈ 66.33cm².

Với thông tin về kích thước của hình hộp chữ nhật, chúng ta có thể dễ dàng tính toán diện tích mặt cầu ngoại tiếp và áp dụng vào các bài toán liên quan.

– Một số ví dụ về bài toán:
1. Hãy tìm diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có các cạnh AB = 5cm, AD = 12cm và AA’ = 10cm.
2. Một hình hộp chữ nhật có cạnh AB = 8m, AD = 6m và AA’ = 12m. Tính toán diện tích mặt cầu ngoại tiếp của khối hộp này.
3. Nếu một khối hộp chữ nhật có các cạnh AB = a, AD = b và AA’ = c. Hãy tìm công thức để tính diện tích mặt cầu ngoại tiếp của khối hộp này dựa trên các kích thước của nó.

Với công thức đã được đề cập, ta có thể áp dụng vào các bài toán về diện tích mặt cầu ngoại tiếp khối hộp chữ nhật để giải quyết và tìm ra kết quả mong muốn.

Tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Để tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật, ta cần biết kích thước của hình hộp chữ nhật đó. Trong trường hợp này, kích thước của hình hộp chữ nhật là a, \(a\sqrt{3}\) và 2a.

Ta xét khối hộp chữ nhật ABCD.A’B’C’D’ có tâm O. Vì O cách đều các đỉnh của khối hộp này, nên mặt cầu ngoại tiếp khối hộp có tâm O. Để tính bán kính R của mặt cầu, ta sử dụng công thức \(R = \frac{AC’}{2}\).

Từ các thông tin đã cho, ta có AC = 2a và AC’ = \(2a\sqrt{2}\). Thay vào công thức bán kính R, ta có: \(R=\frac{AC’}{2}=a\sqrt{2}\).

Do đó, diện tích mặt cầu ngoại tiếp khối hộp chữ nhật này là \(S=4\pi R^{2} = 8\pi a^{2}\).

Ứng dụng của diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật là một đại lượng quan trọng trong các bài toán hình học và các ứng dụng thực tế. Được tính bằng công thức \(S=4\pi R^{2}\), diện tích này giúp ta xác định kích thước và vị trí của mặt cầu ngoại tiếp.

Ứng dụng của diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có thể được thấy trong lĩnh vực kiến trúc, thiết kế đồ họa, công nghệ sản xuất và nhiều lĩnh vực khác. Với kiến thức về diện tích này, chúng ta có thể tính toán và xây dựng các công trình, thiết kế các sản phẩm phù hợp và hiệu quả.

Tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Một khối hộp chữ nhật có kích thước AB = a, AD = \(a\sqrt{3}\) và AA’ = 2a. Khối hộp này có tâm O và mặt cầu ngoại tiếp khối hộp cũng có tâm O. Để tính diện tích mặt cầu ngoại tiếp này, chúng ta cần tìm bán kính R của mặt cầu.

Đầu tiên, ta xác định các giá trị của AC và AC’. Áp dụng định lý Pythagoras, ta có:
AC = \(\sqrt{AB^2 + AD^2} = 2a\)
AC’ = \(\sqrt{AC^2 + CC’^2} = 2a\sqrt{2}\)

Sau đó, ta sử dụng công thức để tính bán kính:
R = \(\frac{AC’}{2} = a\sqrt{2}\)

Cuối cùng, ta tính diện tích S của mặt cầu:
S = \(4\pi R^2 = 8\pi a^2\)

Vậy diện tích mặt cầu ngoại tiếp khối hộp chữ nhật này là 8πa².

Lợi ích của việc biết được diện tích mặt cầu ngoại tiếp

Việc biết được diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có thể giúp ta giải các bài toán liên quan đến không gian và hình học. Bằng việc áp dụng công thức tính diện tích mặt cầu, ta có thể tính toán và xác định được kích thước và vị trí của các khối hộp chữ nhật.

Ngoài ra, việc hiểu về diện tích mặt cầu ngoại tiếp cũng giúp ta hiểu sâu hơn về các khái niệm trong không gian, như bán kính và tâm của một mặt cầu. Điều này có thể ứng dụng trong các lĩnh vực khác nhau như kiến trúc, công nghệ hay thiết kế.

Tổng quan lại, việc biết được diện tích mặt cầu ngoại tiếp là rất hữu ích trong việc giải quyết bài toán không gian và hình học.

1. Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Theo thông tin đã cho, ta biết rằng các đỉnh của khối hộp chữ nhật ABCD.A’B’C’D’ đều cách đều tâm O. Do đó, mặt cầu ngoại tiếp khối hộp có tâm O. Ta có thể tính được bán kính R của mặt cầu này bằng công thức: \( R = \frac{AC’}{2} \). Tiếp theo, ta sẽ tính giá trị của AC’ để từ đó suy ra diện tích mặt cầu ngoại tiếp.

– Bước 1: Tính giá trị AC
Sử dụng công thức Pythagoras, ta có \( AC = \sqrt{AB^2 + AD^2} = 2a \), với a là kích thước của hình hộp chữ nhật.

– Bước 2: Tính giá trị AC’
Từ điểm C, ta vẽ đường cao CL vuông góc và AB. Khi đó, ACL là tam giác vuông tại A.
Áp dụng lại công thức Pythagoras vào tam giác vuông ACL, ta có \( AC’ = \sqrt{AC^2 + CC’^2} = 2a\sqrt{2} \).

– Bước 3: Tính giá trị R
Thay vào công thức \( R = \frac{AC’}{2} \), ta có \( R = a\sqrt{2} \).

– Bước 4: Tính diện tích mặt cầu
Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật là \( S = 4\pi R^2 = 8\pi a^2 \).

2. Quan hệ giữa kích thước hình hộp chữ nhật và diện tích mặt cầu ngoại tiếp

Từ kết quả tính toán ở trên, ta có thể suy ra một quan hệ giữa kích thước của hình hộp chữ nhật và diện tích mặt cầu ngoại tiếp:

– Khi kích thước của hình hộp chữ nhật tăng lên (a tăng), diện tích mặt cầu ngoại tiếp tăng lên theo công thức \( S = 8\pi a^2 \).
– Nếu bán kính của mặt cầu ngoại tiếp là R, ta có quan hệ \( R = a\sqrt{2} \). Từ đó, khi bán kính tăng lên, tức là khi a tăng, diện tích mặt cầu ngoại tiếp sẽ tăng theo công thức \( S = 4\pi R^2 \).

Qua đó, ta nhận thấy sự tương quan giữa kích thước của hình hộp chữ nhật và diện tích mặt cầu ngoại tiếp. Kết quả này có thể được áp dụng trong các bài toán liên quan đến hình học không gian, giúp ta hiểu rõ hơn về mối quan hệ giữa các yếu tố trong không gian.

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Theo thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra diện tích mặt cầu ngoại tiếp khối hộp này. Xét khối hộp chữ nhật ABCD.A’B’C’D’ với tâm O và các cạnh AB = a, AD = a√3, và AA’ = 2a. Do O cách đều các đỉnh của khối hộp, nên mặt cầu ngoại tiếp có tâm là O và bán kính R.

– Đầu tiên, ta tính được AC = √(AB^2 + AD^2) = 2a.
– Tiếp theo, AC’ = √(AC^2 + CC’^2) = 2a√2.
– Vì vậy, bán kính R được tính bằng R = AC’/2 = a√2.
– Từ đó, diện tích mặt cầu ngoại tiếp khối hộp là S = 4πR^2 = 8πa^2.

Vậy, từ thông tin về kích thước của hình hộp chữ nhật ABCD.A’B’C’D’, ta có thể suy ra được diện tích mặt cầu ngoại tiếp khối hộp này là 8πa^2.

Ứng dụng của diện tích mặt cầu ngoại tiếp

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật là một thông tin quan trọng trong việc tính toán và áp dụng vào các bài toán thực tế.

– Trong lĩnh vực xây dựng, kiến thức về diện tích mặt cầu ngoại tiếp giúp trong việc tính toán và thiết kế các công trình có hình dạng hộp chữ nhật. Việc biết được diện tích này sẽ giúp cho các kỹ sư xác định được kích thước và tỷ lệ phù hợp cho công trình.
– Ngoài ra, trong lĩnh vực đồ họa và thiết kế, kiến thức về diện tích mặt cầu ngoại tiếp cũng rất hữu ích. Người thiết kế có thể sử dụng thông tin này để tạo ra các hình ảnh 3D sống động và chân thực.
– Diện tích mặt cầu ngoại tiếp còn có ứng dụng trong các bài toán liên quan đến không gian và giải phẫu. Với kiến thức này, ta có thể xác định được vị trí và khoảng cách của các điểm trên hình hộp chữ nhật.

Tóm lại, hiểu rõ về diện tích mặt cầu ngoại tiếp khối hộp chữ nhật sẽ giúp ta áp dụng kiến thức này vào việc giải quyết các bài toán thực tế và xây dựng các công trình.

1. Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Dựa vào thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra diện tích mặt cầu ngoại tiếp của khối hộp này. Khối hộp chữ nhật có các cạnh là AB = a, AD = a√3 và AA’ = 2a, và tâm của mặt cầu ngoại tiếp khối hộp là O.

2. Tâm và bán kính của mặt cầu ngoại tiếp

Điểm O là tâm của mặt cầu ngoại tiếp khối hộp chữ nhật vì O cách đều các đỉnh của khối hộp này. Bán kính mặt cầu được tính bằng AC’/2, trong đó AC’ là đường chéo của mặt phẳng ABCD.A’B’C’D’. Khi tính toán ta có: AC = 2a và AC’ = 2a√2, do đó bán kính R = AC’/2 = a√2.

3. Diện tích mặt cầu ngoại tiếp

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật được tính bằng công thức S = 4πR^2, trong đó R là bán kính. Sau khi thay giá trị R = a√2 vào, ta có diện tích S = 4π(a√2)^2 = 8πa^2.

Vậy, dựa vào kích thước của hình hộp chữ nhật, ta có thể suy ra được tâm và bán kính của mặt cầu ngoại tiếp khối hộp, cũng như tính được diện tích mặt cầu này. Điều này giúp chúng ta hiểu rõ hơn về tổ chức không gian và các thuộc tính của các hình học trong toán học.

1. Từ kích thước của hình hộp chữ nhật, ta có thể tính được bán kính mặt cầu ngoại tiếp khối hộp

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có thể được suy ra từ thông tin về kích thước của hình hộp. Trước tiên, chúng ta xét khối hộp chữ nhật ABCD.A’B’C’D’ tâm O, với chiều dài AD = a√3, chiều rộng AB = a và chiều cao AA’ = 2a. Ta có thể tìm ra bán kính R của mặt cầu ngoại tiếp khối hộp này.

Đầu tiên, tính đường chéo AC của mặt phẳng đáy ABCD:
\(AC=\sqrt{AB^2+AD^2}=\sqrt{a^2+a^2 \cdot 3}=2a\).

Tiếp theo, tính đường chéo AC’ của mặt phẳng đáy A’B’C’D’:
\(AC’=\sqrt{AC^2+C{{C’}^2}}=\sqrt{(2a)^2+(2a\sqrt{3}/\sqrt{3})^2}=\sqrt{4a^2+\frac{12a^2}{3}}=2a\sqrt{2}\).

Từ đó, suy ra bán kính R của mặt cầu ngoại tiếp khối hộp:
\(R=\frac{AC’}{2}=a\sqrt{2}\).

Vậy, dựa trên thông tin về kích thước của hình hộp chữ nhật, ta có thể tính được bán kính mặt cầu ngoại tiếp khối hộp.

2. Từ bán kính mặt cầu ngoại tiếp khối hộp, ta có thể tính được diện tích mặt cầu

Sau khi đã tìm ra bán kính R của mặt cầu ngoại tiếp khối hộp chữ nhật từ kích thước của hình hộp, chúng ta có thể tính được diện tích mặt cầu.

Diện tích mặt cầu ngoại tiếp khối hộp là tổng diện tích các phần tử nhỏ trên toàn bề mặt của nó. Với bán kính R đã suy ra trước đó (R = a√2), ta có thể áp dụng công thức để tính diện tích mặt cầu như sau:

\(S=4\pi R^2=4\pi (a\sqrt{2})^2=8\pi a^2\).

Vậy, từ bán kính mặt cầu ngoại tiếp khối hộp, ta có thể suy ra được diện tích mặt cầu.

Công thức tính diện tích mặt cầu ngoại tiếp

Để tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật, ta sử dụng công thức sau:

• S = 4πR²

Trong đó, S là diện tích mặt cầu ngoại tiếp và R là bán kính của mặt cầu.

Tính toán bán kính của mặt cầu

Để tính bán kính của mặt cầu ngoại tiếp khối hộp chữ nhật, ta sử dụng các thông tin về kích thước của hình hộp chữ nhật. Với khối hộp chữ nhật ABCD.A’B’C’D’ tâm O có các đỉnh A, B, C, D, A’, B’, C’, D’ và các cạnh AB = a, AD = a√3 và AA’ = 2a. Ta có:

• AABC là tam giác vuông tại A nên AC = √(AB² + AD²) = 2a
• ACC’ là tam giác vuông tại C’ nên AC’ = √(AC² + CC’²) = 2a√2
• Vậy bán kính R của mặt cầu ngoại tiếp khối hộp chữ nhật là R = AC’/2 = a√2

Từ đó, chúng ta có thể suy ra được diện tích mặt cầu ngoại tiếp: S = 4πR² = 8πa².

1. Tính diện tích mặt cầu ngoại tiếp

Từ thông tin về kích thước của hình hộp chữ nhật, ta có thể tính được diện tích mặt cầu ngoại tiếp khối hộp này. Theo thông tin cho trước, ta biết rằng tâm của mặt cầu ngoại tiếp khối hộp là O và bán kính R được xác định bằng công thức R = AC’/2, trong đó AC’ là khoảng cách từ điểm A đến tâm O.

Sau khi tính toán, ta có kết quả R = a√2. Vậy diện tích mặt cầu ngoại tiếp khối hộp chữ nhật này được xác định bằng công thức S = 4πR^2 = 8πa^2.

2. Đặc điểm của khối hộp chữ nhật

Khối hộp chữ nhật ABCD.A’B’C’D’ có các đỉnh A, B, C, D, A’, B’, C’, D’ và tâm O. Khi xét các cạnh và đoạn vuông góc trong khối hộp này, ta có các thông tin sau:
– AB = a là chiều dài của cạnh của hình hộp.
– AD = a√3 là chiều cao (hoặc chiều rộng) của hình hộp.
– AA’ = 2a là đoạn thẳng nối từ đỉnh A đến tâm O.

Thông qua việc xem xét các cạnh và đường chéo của khối hộp chữ nhật này, ta có thể điều tra và rút ra các tính chất và quy luật liên quan đến kích thước và góc trong khối hộp.

1. Ý nghĩa của diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có thể đưa ra thông tin về không gian mà khối hộp chiếm dụng. Nó cho biết diện tích bề mặt cầu mà các điểm trên khối hộp phải đi qua khi được nằm trên 1 lớp cầu có tâm O và bán kính R. Diện tích này có thể được sử dụng để tính toán, so sánh hoặc áp dụng trong các bài toán liên quan đến không gian và hình học.

2. Cách tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Để tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật, ta áp dụng công thức S = 4πR^2, trong đó R là bán kính của mặt cầu. Trong trường hợp này, bán kính R được xác định bằng công thức R = AC’/2, với AC’ là chiều dài đoạn thẳng từ A đến C’ trên khối hộp.

• Bước 1: Tính AC theo công thức AC = √(AB^2 + AD^2).
• Bước 2: Tính diện tích bề mặt của khối hộp chữ nhật thông qua công thức S = 2(AB.AD + AB.AC + AD.AC).
• Bước 3: Tính AC’ theo công thức AC’ = √(AC^2 + CC’^2).
• Bước 4: Áp dụng công thức R = AC’/2 để tính bán kính.
• Bước 5: Tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật theo công thức S = 4πR^2.

Với kích thước a, a√3 và 2a cho khối hộp chữ nhật, ta có diện tích mặt cầu ngoại tiếp là S = 8πa^2. Điều này cho biết rằng diện tích mặt cầu ngoại tiếp sẽ tăng theo bình phương khi kích thước của khối hộp tăng lên.

1. Xác định bán kính mặt cầu ngoại tiếp

Theo thông tin đã cho, ta có thể xác định được bán kính của mặt cầu ngoại tiếp khối hộp chữ nhật. Từ các kích thước của hình hộp ABCD.A’B’C’D’ và biết rằng tâm O cách đều các đỉnh của khối hộp này, ta có thể tính được bán kính \( R \) theo công thức \( R=\frac{AC’}{2} \), trong đó \( AC’ \) là đường chéo của mặt phẳng đi qua tam O và vuông góc với mặt ABCC’.

2. Tính diện tích mặt cầu ngoại tiếp

Với bán kính \( R \) đã được xác định, ta có thể tính diện tích của mặt cầu ngoại tiếp khối hộp chữ nhật. Diện tích \( S \) của mặt cầu ngoại tiếp được tính theo công thức \( S=4\pi R^2 \), trong đó \( \pi \approx 3.14 \). Dựa vào giá trị của \( R \), ta có thể tính toán để thu được diện tích chính xác.

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có thể được suy ra từ thông tin về kích thước của hình hộp chữ nhật. Xét khối hộp chữ nhật ABCD.A’B’C’D’ tâm O, với AB = a, AD = a√3 và AA’ = 2a. Vì O cách đều các đỉnh của khối hộp này, nên mặt cầu ngoại tiếp khối hộp có tâm O và bán kính R = AC’/2.

Tính diện tích mặt cầu

Để tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật, ta cần biết bán kính của mặt cầu. Từ thông tin về kích thước của khối hộp chữ nhật, ta có R = AC’/2 = a√2. Vậy diện tích mặt cầu này là S = 4πR^2 = 8πa^2.

– Được suy ra từ thông tin về kích thước của hình hộp chữ nhật
– Mặt cầu có tâm O và bán kính R
– Diện tích mặt cầu là 8πa^2

Đây là công thức để tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật dựa trên thông tin về kích thước của khối hộp. Công thức này có thể được áp dụng trong các bài toán liên quan đến mặt cầu và hình hộp chữ nhật.

1. Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Trong đề bài, đã cho biết rằng khối hộp chữ nhật có kích thước a, \( a\sqrt{3} \) và 2a. Với thông tin này, chúng ta có thể suy ra được diện tích mặt cầu ngoại tiếp của khối hộp.

Đầu tiên, ta xét khối hộp ABCD.A’B’C’D’ với tâm O. Từ việc AB = a, AD = \( a\sqrt{3} \) và A’A = 2a, ta có thể dễ dàng nhận thấy rằng O cách đều các đỉnh của khối hộp này. Do đó, mặt cầu ngoại tiếp của khối hộp có tâm O.

Tiếp theo, chúng ta sẽ tính bán kính R của mặt cầu ngoại tiếp này. Ta có thể sử dụng công thức R = \(\frac{AC’}{2}\), trong đó AC là khoảng cách từ điểm A đến C’ và AC’ là khoảng cách từ điểm A đến điểm C.

Khi tính toán, ta sẽ thu được AC = 2a và AC’ = \(2a\sqrt{2}\). Thay vào công thức trên, ta có R = \(a\sqrt{2}\). Từ đó, diện tích mặt cầu ngoại tiếp khối hộp chữ nhật này là \(S = 4\pi R^2 = 8\pi a^2\).

2. Đặc điểm của diện tích mặt cầu ngoại tiếp

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có tâm O và bán kính \(a\sqrt{2}\) có một số đặc điểm quan trọng:

1. Diện tích mặt cầu ngoại tiếp không chỉ phụ thuộc vào kích thước của khối hộp chữ nhật, mà còn phụ thuộc vào khoảng cách từ các đỉnh của hình hộp tới tâm O. Trong trường hợp này, ta đã biết rằng O cách đều các đỉnh của khối hộp, do đó diện tích mặt cầu ngoại tiếp là tối đa.

2. Với bán kính \(a\sqrt{2}\), diện tích mặt cầu ngoại tiếp sẽ lớn hơn diện tích bề mặt tổng của các mặt của khối hộp. Điều này cho thấy rằng diện tích mặt cầu ngoại tiếp có khả năng che phủ toàn bộ khối hộp chữ nhật.

3. Diện tích mặt cầu ngoại tiếp không chỉ có ý nghĩa hình học mà còn có thể được áp dụng trong các bài toán liên quan đến khối hộp chữ nhật, như tính toán khoảng cách từ tâm O tới các điểm trên cạnh của khối hộp hoặc tính toán thể tích của khối hộp.

1. Tâm và bán kính mặt cầu ngoại tiếp

Theo thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được thông tin về tâm và bán kính của mặt cầu ngoại tiếp khối hộp này. Giả sử khối hộp chữ nhật có các cạnh AB, AD và AA’ có độ dài lần lượt là a, \(a\sqrt{3}\) và 2a. Với tâm O nằm ở giữa của khối hộp và khoảng cách từ các đỉnh đến tâm này bằng nhau, ta có thể kết luận rằng mặt cầu ngoại tiếp có tâm O.

Bán kính R của mặt cầu ngoại tiếp được tính bằng một nửa đoạn thẳng AC’. Ta biết rằng AC’ là đường chéo của mặt phẳng ABCD.A’B’C’D’, và theo công thức Pythagoras ta có AC’ = \(2a\sqrt{2}\). Do đó, bán kính R = AC’/2 = \(a\sqrt{2}\).

2. Diện tích mặt cầu ngoại tiếp

Để tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật, ta sử dụng công thức \(S = 4\pi R^2\), trong đó S là diện tích mặt cầu, π là số Pi (xấp xỉ 3.14) và R là bán kính.

Substituting the value of R as \(a\sqrt{2}\), we can calculate the surface area of the circumscribed sphere. Therefore, \(S = 4\pi \times (a\sqrt{2})^2 = 8\pi a^2\).

Vậy diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước a, \(a\sqrt{3}\) và 2a là 8πa^2.

This information about the surface area of the circumscribed sphere provides insights into the geometric properties and relationships between different elements of rectangular prism within which it is inscribed.

Sự liên quan giữa kích thước của hình hộp chữ nhật và diện tích mặt cầu ngoại tiếp

Thông qua thông tin về kích thước của hình hộp chữ nhật, chúng ta có thể suy ra một số điều về diện tích mặt cầu ngoại tiếp. Xét khối hộp chữ nhật ABCD.A’B’C’D’ tâm O, với AB = a, AD = a√3 và AA’ = 2a. Do O cách đều các đỉnh của khối hộp này, ta có thể xác định được rằng mặt cầu ngoại tiếp khối hộp có tâm O và bán kính R=AC’/2.

Suy ra diện tích mặt cầu ngoại tiếp

Để tính diện tích mặt cầu ngoại tiếp của khối hộp chữ nhật này, ta cần xác định giá trị của R. Theo công thức, AC = √(AB^2 + AD^2) = 2a và AC’ = √(AC^2 + CC’^2) = 2a√2. Từ đó suy ra R=AC’/2=a√2.

Vì vậy, diện tích mặt cầu ngoại tiếp là S=4πR^2=8πa^2.

Tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Để tính diện tích mặt cầu ngoại tiếp của khối hộp chữ nhật có kích thước a, \( a\sqrt{3} \) và 2a, ta xét khối hộp ABCD.A’B’C’D’ có tâm O. Các đỉnh của khối hộp này cách nhau một khoảng đều, do đó tâm O cũng cách đều các đỉnh. Chúng ta biết rằng mặt cầu ngoại tiếp khối hộp có tâm O và bán kính \( R=\frac{AC’}{2} \).

Trước tiên, chúng ta tính giá trị AC theo công thức chuẩn: \( AC=\sqrt{AB^2+AD^2}=2a \). Tiếp theo, chúng ta tính giá trị AC’ theo công thức Pitago: \( AC’=\sqrt{AC^2+C’C’^2}=\sqrt{(2a)^2+(a\sqrt{2})^2}=2a\sqrt{2} \). Dễ dàng suy ra rằng \( R=\frac{AC’}{2}=a\sqrt{2} \).

Vậy diện tích mặt cầu ngoại tiếp của khối hộp này là \( S=4\pi R^2=4\pi (a\sqrt{2})^2=8\pi a^2 \).

Ứng dụng của diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có thể được sử dụng trong nhiều lĩnh vực khác nhau. Dưới đây là một số ứng dụng của kiến thức này:

1. Xây dựng: Khi thiết kế các công trình xây dựng, diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có thể giúp xác định không gian cần thiết cho việc tạo ra các yếu tố hình học phù hợp.

2. Công nghệ: Trong lĩnh vực công nghệ, kiến thức về diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có thể được áp dụng để tính toán và thiết kế các bề mặt cong, ví dụ như ống và đường ống.

3. Giáo dục: Hiểu biết về diện tích mặt cầu ngoại tiếp khối hộp chữ nhật giúp sinh viên và học sinh hiểu rõ hơn về các thuộc tính hình học của các đa diện, từ đó áp dụng vào việc giải quyết các bài toán liên quan đến hình học.

Kích thước của hình hộp chữ nhật

Trong đề bài, ta biết rằng kích thước của hình hộp chữ nhật là a, \( a\sqrt{3} \) và 2a. Kích thước này cung cấp thông tin về các cạnh và đường chéo của hình hộp chữ nhật.

– Cạnh AB có độ dài a.
– Cạnh AD có độ dài \( a\sqrt{3} \).
– Đường chéo AC có độ dài 2a.

Mặt cầu ngoại tiếp khối hộp

Dựa vào thông tin về kích thước hình hộp chữ nhật, ta có thể suy ra các thuộc tính của mặt cầu ngoại tiếp.

1. Tâm O: Vì O cách đều các điểm A, B, C, D nên O là tâm của mặt cầu ngoại tiếp khối hộp.
2. Bán kính R: Để tính bán kính, ta sử dụng công thức \( R=\frac{AC’}{2} \). Thay giá trị vào ta được \( R=a\sqrt{2} \).

Với các giá trị tìm được về tâm và bán kính, ta có thể tính diện tích mặt cầu ngoại tiếp.

– Diện tích S: Sử dụng công thức \( S=4\pi {{R}^{2}} \), ta tính được \( S=8\pi {{a}^{2}} \).

Tóm lại, từ thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được tâm và bán kính của mặt cầu ngoại tiếp khối hộp, từ đó tính được diện tích mặt cầu ngoại tiếp.

Suy ra được diện tích mặt cầu ngoại tiếp

Theo thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được diện tích mặt cầu ngoại tiếp.

Đầu tiên, xét khối hộp chữ nhật ABCD.A’B’C’D’ tâm O, với các cạnh AB = a, AD = a√3 và AA’ = 2a. Các đỉnh của khối hộp này đều cách tâm O một khoảng bằng nhau. Do đó, tâm của mặt cầu ngoại tiếp khối hộp là O.

Tiếp theo, ta tính toán bán kính R của mặt cầu ngoại tiếp. Ta có AC = √(AB^2 + AD^2) = 2a và AC’ = √(AC^2 + CC’^2) = 2a√2. Vậy bán kính R sẽ bằng R=AC’/2 = a√2.

Cuối cùng, từ công thức diện tích mặt cầu S=4πR^2, ta thay vào giá trị R=a√2 và tính được S = 8πa^2.

Vậy diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước a, a√3 và 2a là S=8πa^2.

Ứng dụng của diện tích mặt cầu ngoại tiếp

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có thể được áp dụng trong nhiều lĩnh vực. Dưới đây là một số ứng dụng của diện tích này:

1. Xây dựng công trình: Khi thiết kế các tòa nhà, kiến trúc sư và kỹ sư cần biết diện tích mặt cầu ngoại tiếp khối hộp chữ nhật để tính toán các thông số quan trọng, như lượng vật liệu cần sử dụng và chi phí xây dựng.

2. Công nghệ 3D: Trong công nghệ 3D, diện tích mặt cầu ngoại tiếp khối hộp chữ nhật được sử dụng để tạo ra các hình dạng phức tạp và đồ họa chân thực. Đây là một yếu tố quan trọng để tạo ra hiệu ứng thị giác hấp dẫn và chân thực cho các ứng dụng đồ họa và game.

3. Tính toán không gian: Trong lĩnh vực đo lường không gian và thiết kế, diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có thể được sử dụng để tính toán kích thước và khoảng cách giữa các vật thể trong không gian. Điều này đặc biệt hữu ích trong ngành công nghiệp và xây dựng.

4. Giải toán hình học: Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật là một khái niệm quan trọng trong giải toán hình học. Nó cho phép chúng ta tính toán các thông số liên quan đến không gian và hình dạng của các đối tượng, từ đó giúp giải quyết các bài toán và vấn đề liên quan đến hình học.

1. Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước a, \( a\sqrt{3} \) và 2a

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước a, \( a\sqrt{3} \) và 2a là \( S=4\pi {{R}^{2}}=8\pi {{a}^{2}} \). Trong đó, R là bán kính của mặt cầu ngoại tiếp khối hộp chữ nhật này. Để tìm được bán kính, ta xét khối hộp chữ nhật ABCD.A’B’C’D’ với tâm O. Các đỉnh của khối hộp này cách đều tới tâm O, do đó tâm O của mặt cầu nằm giữa các đỉnh A, B, C, D.

2. Xét khối hộp chữ nhật ABCD.A’B’C’D’ tâm O

Xét khối hộp chữ nhật ABCD.A’B’C’D’ có tâm O. Khi xét các cạnh của khối hộp này, ta biết rằng AB = a, AD = \(a\sqrt{3}\), và AA’ = 2a. Từ đây suy ra AC = \(\sqrt{AB^2 + AD^2}\) = 2a và AC’ = \(\sqrt{AC^2 + CC’^2}\) = 2a\sqrt{2}.

3. Bán kính mặt cầu ngoại tiếp khối hộp

Do tâm O của mặt cầu nằm giữa các đỉnh A, B, C, D, ta có bán kính R của mặt cầu ngoại tiếp khối hộp là \(R=\frac{AC’}{2}\) = a\sqrt{2}.

Từ đó, suy ra diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước a, \( a\sqrt{3} \) và 2a là \(S=4\pi {{R}^{2}}=8\pi {{a}^{2}}\)

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Công thức tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước a, \( a\sqrt{3} \) và 2a là \( S=4\pi {{R}^{2}}=8\pi {{a}^{2}} \). Để hiểu về công thức này, ta phân tích từng thành phần trong công thức.

Đầu tiên, ta có tâm của mặt cầu ngoại tiếp khối hộp chữ nhật là điểm O. Từ thông tin cho trước, O cách đều các đỉnh của khối hộp ABCD.A’B’C’D’, do đó tâm của mặt cầu nằm giữa các đỉnh này.

Tiếp theo, để tính bán kính R của mặt cầu, ta sử dụng thông tin về chiều dài AC’. Qua việc tính toán dựa trên công thức Pythagoras và các định lý liên quan, ta suy ra rằng \( AC’=\sqrt{A{{C}^{2}}+C{{{{C}’}}^{2}}}=2a\sqrt{2} \).

Cuối cùng, áp dụng vào công thức diện tích mặt cầu \( S=4\pi {{R}^{2}} \), ta thu được kết quả là \( S=8\pi {{a}^{2}} \). Đây chính là diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước đã cho.

Tóm tắt

Từ thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được diện tích mặt cầu ngoại tiếp. Tâm của mặt cầu nằm ở giữa các đỉnh của khối hộp và bán kính được tính theo chiều dài AC’. Cuối cùng, công thức diện tích mặt cầu sử dụng bán kính này để tính toán. Kết quả cuối cùng là diện tích mặt cầu ngoại tiếp của khối hộp chữ nhật.

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Công thức để tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật là \(S=4\pi R^2\), trong đó \(R\) là bán kính của mặt cầu. Từ thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra bán kính \(R\) của mặt cầu.

Tâm và bán kính của mặt cầu ngoại tiếp khối hộp

Tâm của mặt cầu ngoại tiếp khối hộp chữ nhật là điểm O nằm ở giữa các đỉnh A, B, C, D. Bán kính \(R\) được tính bằng công thức \(R = \frac{AC’}{2}\), trong đó \(AC’\) là khoảng cách từ tâm O đến đỉnh C’.

Diện tích mặt cầu ngoại tiếp khối hộp

Khi đã biết bán kính \(R\), ta có thể tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật theo công thức \(S = 4\pi R^2\). Thay vào giá trị của bán kính \(R\) trong công thức này, ta sẽ có diện tích của mặt cầu.

Như vậy, thông qua các thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được tâm và bán kính của mặt cầu ngoại tiếp khối hộp, từ đó tính được diện tích của mặt cầu.

Từ thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được diện tích mặt cầu ngoại tiếp

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có thể được suy ra từ thông tin về kích thước của hình hộp. Xét khối hộp ABCD.A’B’C’D’ có tâm O, với các cạnh AB = a, AD = \(a\sqrt{3}\), và A’A = 2a. Vì O cách đều các đỉnh của khối hộp này, ta có thể biết rằng mặt cầu ngoại tiếp khối hộp có tâm O và bán kính \(R=\frac{AC’}{2}\).

Để tính diện tích mặt cầu ngoại tiếp này, ta sử dụng các giá trị đã biết: AC = \(2a\) và AC’ = \(2a\sqrt{2}\). Từ đó, ta có \(R=\frac{AC’}{2}=a\sqrt{2}\). Diện tích mặt cầu ngoại tiếp khối hộp là \(S=4\pi R^2=8\pi a^2\).

Với các thông tin trên, ta có thể suy ra diện tích mặt cầu ngoại tiếp từ kích thước của hình hộp chữ nhật.

Mặt cầu ngoại tiếp khối hộp chữ nhật có tâm O

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật được suy ra từ thông tin về kích thước của hình hộp chữ nhật. Xét khối hộp chữ nhật ABCD.A’B’C’D’ với tâm O, và các chiều dài của các cạnh là AB = a, AD = a√3, và AA’ = 2a. Do O cách đều các đỉnh của khối hộp này, ta có thể suy ra rằng mặt cầu ngoại tiếp khối hộp có tâm O.

Bán kính và diện tích mặt cầu ngoại tiếp

Bán kính của mặt cầu ngoại tiếp được tính bằng AC’/2, trong đó AC là đường chéo của mặt phẳng ABCD và C’ là trung điểm của AC. Ta có thể tính toán bán kính theo công thức sau: R = AC’/2 = a√2.

Từ bán kính đã tính được, ta có thể suy ra diện tích mặt cầu ngoại tiếp khối hộp. Diện tích S được tính theo công thức S = 4πR^2. Như vậy, diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước a, a√3, và 2a là S = 4π(a√2)^2 = 8πa^2.

Trên đây là thông tin về diện tích mặt cầu ngoại tiếp khối hộp chữ nhật dựa trên thông tin về kích thước của hình hộp chữ nhật.

Diện tích mặt cầu ngoại tiếp

Khi có thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được diện tích mặt cầu ngoại tiếp khối hộp này. Với khối hộp chữ nhật ABCD.A’B’C’D’ có tâm O, ta biết rằng O cách đều các đỉnh của khối hộp này. Do đó, mặt cầu ngoại tiếp khối hộp có tâm O và bán kính R bằng một nửa đoạn AC’. Để tính toán diện tích mặt cầu, ta cần biết giá trị của AC’.

Tính toán diện tích mặt cầu

Để tính toán diện tích mặt cầu, ta sử dụng công thức S = 4πR^2. Ta đã biết rằng AC’ = 2a√2 và R = AC’/2 = a√2. Thay vào công thức, ta có S = 4π(a√2)^2 = 8πa^2.

Vậy diện tích mặt cầu ngoại tiếp khối hộp chữ nhật với kích thước a, a√3 và 2a là 8πa^2.

1. Suy ra được diện tích mặt cầu

Từ thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được diện tích mặt cầu ngoại tiếp khối hộp này. Khối hộp chữ nhật ABCD.A’B’C’D’ có tâm O, với đỉnh A có tọa độ (0,0,0), AB = a và AD = a√3. Mặt cầu ngoại tiếp khối hộp này có tâm O và bán kính R.

2. Xác định bán kính mặt cầu ngoại tiếp

Để xác định bán kính R của mặt cầu ngoại tiếp khối hộp chữ nhật ABCD.A’B’C’D’, ta sử dụng công thức bán kính mặt cầu ngoại tiếp tam giác vuông ABC: R = AC’/2. Ta tính được AC = 2a và AC’ = 2a√2 từ các giá trị đã cho. Sau đó, áp dụng công thức để tính gia trị bán kính R.

3. Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Với bán kính R đã xác định được, ta có thể tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật ABCD.A’B’C’D’. Sử dụng công thức diện tích mặt cầu: S = 4πR^2, ta thay vào giá trị của R đã tính được từ bước trước. Kết quả là diện tích của mặt cầu ngoại tiếp.

1. Diện tích mặt cầu ngoại tiếp

Theo thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được diện tích mặt cầu ngoại tiếp khối hộp chữ nhật này. Xét khối hộp chữ nhật ABCD.A’B’C’D’ có tâm O, với các cạnh AB = a, AD = \(a\sqrt{3}\) và AA’ = 2a. Do O cách đều các đỉnh của khối hộp này, ta có thể biết rằng mặt cầu ngoại tiếp khối hộp có tâm là O và bán kính R = \(\frac{AC’}{2}\).

2. Tính toán bán kính

Để tính toán bán kính của mặt cầu ngoại tiếp khối hộp chữ nhật, ta sẽ dựa vào các giá trị đã cho. Cần tính AC và AC’, sau đó lấy AC’ chia cho 2 để thu được bán kính R. Theo công thức Pythagoras, ta có:

\(AC=\sqrt{AB^2 + AD^2} = 2a\)

\(AC’=\sqrt{AC^2 + C{{C’}^2}}= 2a\sqrt{2}\)

Sau khi tính toán, bán kính R của mặt cầu ngoại tiếp khối hộp chữ nhật này được cho bằng \(a\sqrt{2}\).

3. Diện tích mặt cầu ngoại tiếp

Với đã biết giá trị của bán kính R, ta có thể tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật. Diện tích S của mặt cầu ngoại tiếp được tính bằng công thức \(S = 4\pi R^2\). Thay vào giá trị của R, ta có:

\(S = 4\pi (a\sqrt{2})^2 = 8\pi a^2 \)

Vậy diện tích mặt cầu ngoại tiếp khối hộp chữ nhật này là 8πa^2.

Tính diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Theo thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được diện tích mặt cầu ngoại tiếp. Xét khối hộp chữ nhật ABCD.A’B’C’D’ có tâm O, với các cạnh AB = a, AD = \(a\sqrt{3}\) và AA’ = 2a. Vì O cách đều các đỉnh của khối hộp này, nên ta có thể xác định được mặt cầu ngoại tiếp khối hộp có tâm O.

Để tính diện tích mặt cầu ngoại tiếp này, ta sẽ sử dụng công thức \( R=\frac{AC’}{2} \), trong đó AC là khoảng cách từ A đến C và AC’ là khoảng cách từ A đến C’. Ta đã biết rằng AC = 2a và AC’ = \(2a\sqrt{2}\), vậy \( R=\frac{AC’}{2}=a\sqrt{2} \).

Vậy diện tích mặt cầu ngoại tiếp khối hộp chữ nhật này là \( S=4\pi R^2=8\pi a^2 \).

Ứng dụng trong giảng dạy toán online

Thông qua việc giảng dạy toán online qua ứng dụng như Zoom, Google Meet,… giáo viên có thể trực tiếp thể hiện và giải thích các bài toán liên quan đến diện tích mặt cầu ngoại tiếp khối hộp chữ nhật. Từ thông tin về kích thước của hình hộp chữ nhật, giáo viên có thể giúp học sinh hiểu rõ và áp dụng công thức để tính diện tích mặt cầu ngoại tiếp.

Ngoài ra, việc sử dụng công nghệ trong việc giảng dạy toán online tương tác 1 thầy 1 trò cũng mang lại nhiều lợi ích cho học sinh. Họ có thể được hỗ trợ trực tuyến 24/7 và sự linh hoạt trong lịch học từ sáng đến tối cũng như từ thứ hai đến chủ nhật. Điều này giúp tăng cường khả năng hiểu và áp dụng kiến thức toán học của học sinh.

Lưu ý: Bạn cần điền email để bình luận.

1. Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Trong đề bài đã cho biết, khối hộp chữ nhật có các kích thước là a, \( a\sqrt{3} \) và 2a. Ta cần tìm diện tích mặt cầu ngoại tiếp của khối hộp này.

Với thông tin từ đề, ta xác định được điểm O là tâm của mặt cầu ngoại tiếp khối hộp chữ nhật ABCD.A’B’C’D’. Vì O cách đều các đỉnh của khối hộp này, nên ta có thể suy ra rằng mặt cầu ngoại tiếp có tâm O.

Để tính diện tích mặt cầu ngoại tiếp, ta sử dụng công thức: \( S = 4\pi R^2 \). Trong trường hợp này, bán kính R được tính bằng nửa chiều dài AC’, với \( AC’ = 2a\sqrt{2} \). Từ đó suy ra \( R = \frac{AC’}{2}=a\sqrt{2} \).

Thay giá trị bán kính vào công thức diện tích mặt cầu, ta có: \( S=4\pi {{R}^{2}}=8\pi {{a}^{2}} \).

Nghĩa là diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước a, \( a\sqrt{3} \) và 2a là 8πa^2.

2. Ứng dụng của diện tích mặt cầu ngoại tiếp

Diện tích mặt cầu ngoại tiếp của khối hộp chữ nhật không chỉ có giá trị lý thuyết trong toán học, mà còn được áp dụng rộng rãi trong các lĩnh vực khác nhau.

– Trong xây dựng: Diện tích mặt cầu ngoại tiếp được sử dụng để tính toán và thiết kế các công trình kiến trúc, đảm bảo độ chính xác và sự đẹp mắt cho công trình.
– Trong thiết kế sản phẩm: Khi thiết kế sản phẩm có hình dạng cầu, diện tích mặt cầu ngoại tiếp là yếu tố quan trọng để định lượng và quyết định về tỉ lệ sản phẩm.
– Trong khoa học và công nghệ: Diện tích mặt cầu ngoại tiếp được sử dụng trong việc tạo ra các máy móc và thiết bị công nghệ cao, giúp tăng hiệu suất và hiệu quả của các thiết bị này.

Tổng hợp lại, diện tích mặt cầu ngoại tiếp không chỉ có giá trị trong lý thuyết toán học mà còn mang lại nhiều ứng dụng trong thực tế.

Kích thước của hình hộp chữ nhật

Trong bài toán này, ta đã được cho biết kích thước của hình hộp chữ nhật ABCD.A’B’C’D’. Theo đó, cạnh AB có độ dài a, cạnh AD có độ dài \(a\sqrt{3}\), và cạnh AA’ có độ dài 2a. Nhờ thông tin về kích thước này mà ta có thể suy ra được nhiều điều về diện tích mặt cầu ngoại tiếp khối hộp.

Mặt cầu ngoại tiếp khối hộp

Một trong những điều quan trọng mà ta có thể suy ra từ các kích thước của hình hộp chữ nhật là mặt cầu ngoại tiếp khối hộp có tâm O và bán kính \(R=\frac{AC’}{2}\). Điều này xuất phát từ việc O cách đều các đỉnh của khối hộp ABCD.A’B’C’D’.

Diện tích mặt cầu ngoại tiếp

Khi đã biết được bán kính R của mặt cầu ngoại tiếp khối hộp, ta có thể tính được diện tích của mặt cầu này. Diện tích mặt cầu ngoại tiếp khối hộp ABCD.A’B’C’D’ là \(S=4\pi R^2 = 8\pi a^2\).

Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật

Khi có thông tin về kích thước của hình hộp chữ nhật, ta có thể suy ra được diện tích mặt cầu ngoại tiếp khối hộp đó. Để minh hoạ điều này, xét khối hộp chữ nhật ABCD.A’B’C’D’ với tâm O. Các cạnh của khối hộp là AB = a, AD = \(a\sqrt{3}\) và \(AA’\)= 2a.

Đầu tiên, ta nhận thấy rằng tâm O cách đều các đỉnh của khối hộp này. Vì vậy, mặt cầu ngoại tiếp khối hộp chữ nhật sẽ có tâm O.

Để tính diện tích mặt cầu ngoại tiếp này, ta cần biết bán kính R. Ta có thể tính bán kính R bằng công thức \(R=\frac{AC’}{2}\). Theo tỷ lệ Pythagoras, ta có \(AC=\sqrt{AB^2 + AD^2}= 2a\) và \(AC’=\sqrt{AC^2+CC’^2}= 2a\sqrt{2}\).

Từ đó, ta suy ra được rằng bán kính R là \(a\sqrt{2}\). Vậy diện tích mặt cầu ngoại tiếp khối hộp chữ nhật là \(S=4\pi R^2=8\pi a^2\).

Nhận xét: Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có tỷ lệ thuận với bình phương của kích thước cạnh a. Nếu kích thước cạnh a tăng, diện tích mặt cầu ngoại tiếp sẽ tăng theo tỉ lệ bình phương.

Tổng kết, diện tích hình cầu ngoại tiếp hình hộp chữ nhật là một đường tròn có bán kính bằng nửa đường chéo của hình chữ nhật. Điều này cho phép chúng ta tính toán diện tích của hình cầu dễ dàng thông qua công thức A = 4πR^2, trong đó R là bán kính của hình cầu. Bằng cách áp dụng các công thức và quy tắc liên quan, ta có thể tính toán diện tích của hình cầu ngoại tiếp cho bất kỳ hình hộp chữ nhật nào.