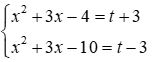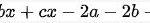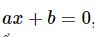Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp và bài tập có lời giải

Bài viết bao gồm cả lý thuyết và bài tập về phân tích đa thức thành nhân tử bằng việc phối hợp các phương pháp. Phần lý thuyết có đầy đủ các công thức và tính chất các em đã được học để áp dụng làm các bài tập. Các bài tập đều có hướng dẫn giải giúp các em có hướng làm bài và vận dụng tốt để làm những bài sau.

Tham khảo thêm:

Trung bình cộng là gì? Khái niệm trung bình cộng và bài tập có lời giải chính xác 100%
Hỗn số là gì? Cách chuyển đổi của hỗn số và bài tập chính xác 100%
Công thức tính đường trung tuyến trong tam giác và bài tập có lời giải từ A-Z

Quý tắc phân tích đa thức thành nhân tử bằng phối hợp nhiều phương pháp 

Ta tìm hướng giải bằng cách đọc kỹ đề bài và rút ra nhận xét để vận dụng các phương pháp đã biết:

• Đặt nhân tử chung
• Dùng hằng đẳng thức
• Nhóm nhiều hạng tử và phối hợp chúng

⇒ Để phân tích đa thức thành nhân tử.

Chú ý: Nếu các hạng tử của đa thức có nhân tử chung thì ta nên đặt nhân tử chung ra ngoài dấu ngoặc để đa thức trong ngoặc đơn giản hơn rồi mới tiếp tục phân tích đến kết quả cuối cùng.

Các dạng toán phân tích đa thức thành nhân tử bằng phương pháp phối hợp

Bài tập 1: Phân tích đa thức thành nhân tử

a) Ta có: ( ab – 1 )² + ( a + b )² = a²b² – 2ab + 1 + a² + 2ab + b²

= a²b² + a² + b² + 1 = ( a²b² + a² ) + ( b² + 1 )

= a²( b² + 1 ) + ( b² + 1 ) = ( a² + 1 )( b² + 1 )

b) Ta có: x³ + 2x² + 2x + 1 = ( x³ + 1 ) + ( 2x² + 2x )

= ( x + 1 )( x² – x + 1 ) + 2x( x + 1 ) = ( x + 1 )( x² + x + 1 )

c) Ta có: x² – 2x – 4y² – 4y = ( x² – 4y² ) – ( 2x + 4y )

= ( x – 2y )( x + 2y ) – 2( x + 2y )

= ( x + 2y )( x – 2y – 2 ).

Bài tập 2: Tính giá trị của biểu thức sau A = x⁶ – 2x⁴ + x³ + x² – x, biết x³ – x = 6.

a, Ta có: A = x⁶ – 2x⁴ + x³ + x² – x = ( x⁶ – 2x⁴ + x² ) + ( x³ – x )

= ( x³ – x )² + ( x³ – x )

Với x³ – x = 6 = ( x³ – x )² + ( x³ – x ), ta có A = 6² + 6 = 36 + 6 = 42.

Vậy A = 42.

b, Giá trị của biểu thức A = x² – 4y² + 4x + 4 tại x = 62, y = -18 là

Ta có A = x² – 4y² + 4x + 4

= (x² + 4x + 4) – 4y² = (x + 2)² – (2y)²

= (x + 2 – 2y)(x + 2 + 2y)

Thay x = 62; y = -18 ta được

A = (62 + 2 – 2.(-18))(62 + 2 + 2.(-18)) = 100.28 = 2800

c, Giá trị của biểu thức B = x³ + x²y – xy² – y³ tại x = 3,25 ; y = 6,75 là

Ta có B = x³ + x²y – xy² – y³

= x²(x + y) – y²(x + y) = (x² – y²)(x + y)

= (x – y)(x + y)(x + y) = (x – y)(x + y)²

Thay x = 3,25 ; y = 6,57 ta được

B = (3,25 – 6,75)(3,25 + 6,75)² = -3,5.10² = -350

Bài tập 3: Tìm x biết

a) (2x – 1)² – (x + 3)² = 0

[(2x – 1) – (x + 3)][(2x – 1) + (x + 3)] = 0

(2x – 1 – x – 3)(2x – 1 + x + 3) = 0

(x – 4)(3x + 2) = 0

Hoặc x – 4 = 0 ⇒ x = 4

Hoặc 3x + 2 = 0 ⇒ 3x = 2 => x = -2/3

Vậy x = 4; x = -2/3.

b) x²(x – 3) + 12 – 4x = 0

x²(x – 3) – 4(x -3)= 0

(x – 3)(x²– 2²) = 0

(x – 3)(x – 2)(x + 2) = 0

Hoặc x – 3 = 0 => x = 3

Hoặc x – 2 =0 => x = 2

Hoặc x + 2 = 0 => x = -2

Vậy x = 3; x = 2; x = -2

c, 2(x + 3) – x² – 3x = 0

⇔ 2(x + 3) – x² – 3x = 0

⇔ 2(x + 3) – (x² + 3x) = 0

⇔ 2(x + 3) – x(x + 3) = 0

⇔ (2 – x)(x + 3) = 0

Vậy x= 2 và x= -3

Bài tập 4: 

a, Ta có (x + 2)(x + 3)(x + 4)(x + 5) – 24 = (x² + 7x + a)(x² + 7x + b) với a, b là các số nguyên và a < b. Khi đó a – b bằng

Ta có T = (x + 2)(x + 3)(x + 4)(x + 5) – 24

= [(x + 2)(x + 5)].[(x + 3)(x + 4)] – 24

= (x² + 7x + 10).(x² + 7x + 12) – 24

Đặt x² + 7x + 11= t, ta được

T = (t – 1)(t + 1) – 24 = t² – 1 – 24 = t² – 25 = (t – 5)(t + 5)

Thay t = x² + 7x + 11, ta được

T = (t – 5)(t + 5) = (x² + 7x + 11 – 5)( x² + 7x + 11 + 5)

= (x² + 7x + 6)( x² + 7x + 16)

Suy ra a = 6; b = 16 ⇒ a – b = -10

b, Ta có (x – 1)(x – 2)(x + 4)(x + 5) – 27 = (x² + 3x + a)(x² + 3x + b) với a, b là các số nguyên. Khi đó a + b bằng

Gọi T = (x – 1)(x – 2)(x + 4)(x + 5) – 27

= [(x – 1)(x + 4)].[(x – 2)(x + 5)] – 27

= (x² + 3x – 4).(x² + 3x – 10) – 27

Đặt x² + 3x – 7 = t ⇒   

Từ đó ta có T = (t – 3)(t + 3) – 27 = t² – 9 – 27 = t² – 36 = (t – 6)(t + 6)

Thay t = x² + 3x – 7 ta được

T = (x² + 3x – 7 – 6)( x² + 3x – 7 + 6)

= (x² + 3x – 13)( x² + 3x – 1) suy ra a = -13; b = -1 ⇒ a + b = -14

Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình