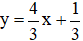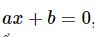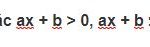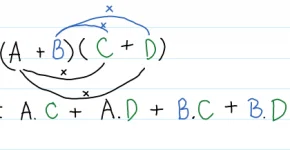Lý thuyết phương trình bậc nhất hai và cách giải phương trình bậc nhất hai ẩn kèm bài tập
Phương trình bấc nhất hai ẩn là dạng toán điển hình của chương trình THPT. Đây là phần kiến thức từ lớp 9 nhưng khi lên lớp 10 thì dạng này phức tạp hơn, các dạng bài ứng dụng thực tế thiếu hơn và đòi hỏi các em thực sự hiểu về nó. Trong bài này, chúng tôi sẽ tổng hợp các lý thuyết và dạng toán điển hình của phương trình trong bài viết dưới đây
Tham khảo thêm:
- Trung bình cộng là gì? Khái niệm trung bình cộng và bài tập có lời giải chính xác 100%
- Nhân đa thức với đa thức là gì? Quy tắc nhân đa thức với đa thức và bài tập có lời giải chính xác 100%
- Chia đa thức với đơn thức là gì? Quy tắc chia đa thức với đơn thức và bài tập có lời giải chính xác 100%
Nội Dung
Phương trình bậc nhất hai ẩn là gì?
Phương trình bậc nhất hai ẩn x, y là hệ thức có dạng: ax + by = c, trong đó a, b, c là các số đã biết (trong đó a ≠ 0 hoặc b ≠ 0 ).
Trong phương trình ax + by = c, nếu giá trị của vế trái tại x = x0 và y =y0 bằng vế phải thì cặp số (x0; y0) được gọi là một nghiệm của phương trình.
Chú ý: Trong mặt phẳng tọa độ Oxy mỗi nghiệm của phương trình ax + by = c được biểu diễn bởi một điểm. Nghiệm (x0; y0) được biểu diễn bởi điểm có tọa độ (x0; y0).
Ví dụ: Các phương trình bậc nhất hai ẩn là 2x + y = 1; x – y = 2; ….
Tập nghiệm của phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn ax + by = c luôn có vô số nghiệm. Tập nghiệm của nó được biểu diễn bởi đường thẳng ax + by = c kí hiệu là (d).
- Nếu a ≠ 0 và b = 0 thì phương trình có nghiệm thì với x = c/a; y ∈ R và đường thẳng d song song hoặc trùng với trục tung.
- Nếu a = 0 và b≠ 0 thì phương trình có nghiệm với x ∈ R; y = c/b và đường thẳng d song song hoặc trùng với trục hoành.
- Nếu a ≠ 0 và b ≠ 0 thì phương trình có nghiệm với x R; y= (-a/b)x + c/b và đường thẳng d là đồ thị hàm số y= (-a/b)x + c/b
Các dạng bài tâp thường gặp ở phương trình hai ẩn
Dạng 1: Tìm điều kiện của tham số để một cặp số cho trước là nghiệm của phương trình bậc nhất hai ẩn.
Phương pháp:: Nếu cặp số thực (x0;y0) thảo mãn ax + by = c thì nó được gọi là nghiệm của phương trình ax + by = c
Bài 1: Trong các cặp số (-2; 1), (0; 2), (-1; 0), (1, 5; 3) và (4; -3) cặp số nào là nghiệm của phương trình:
a) 5x + 4y = 8? ; b) 3x + 5y = -3?
Giải:
a) Xét cặp (-2; 1). Thay x = -2 ; y = 1 vào phương trình 5x + 4y = 8 ta được :
5x + 4y = 5.(-2) + 4.1 = -10 + 4 = -6 ≠ 8
⇒ cặp số (-2; 1) không là nghiệm của phương trình 5x + 4y = 8.
Xét cặp(0; 2). Thay x = 0 ; y = 2 vào phương trình 5x + 4y = 8 ta được
5x + 4y = 5.0 + 4.2 = 8
⇒ cặp số (0; 2) là nghiệm của phương trình 5x + 4y = 8.
Xét cặp (-1; 0). Thay x = -1 ; y = 0 vào phương trình 5x – 4y = 8 ta được:
5x + 4y = 5.(-1) + 4.0 = -5 ≠ 8
⇒ cặp số (-1; 0) không là nghiệm của phương trình 5x + 4y = 8.
Xét cặp (1,5 ; 3). Thay x = 1,5 ; y = 3 vào phương trình 5x + 4y = 8 ta được
5x + 4y = 5.1,5 + 4.3 = 7,5 + 12 = 19,5 ≠ 8
⇒ (1,5; 3) không là nghiệm của phương trình 5x + 4y = 8.
Xét cặp (4;-3).Thay x = 4 ; y = -3 vào phương tình 5x + 4y = 8 ta được:
5x + 4y = 5.4 + 4.(-3) = 20 – 12 = 8
⇒ (4; -3) là nghiệm của phương trình 5x + 4y = 8.
Vậy có hai cặp số (0; 2) và (4; -3) là nghiệm của phương trình 5x + 4y = 8.
b) Xét cặp số (-2; 1).Thay x = -2 ; y = 1 vào phương trình 3x + 5y = -3 ta được:
3x + 5y = 3.(-2) + 5.1 = -6 + 5 = -1 ≠ -3
⇒ (-2; 1) không là nghiệm của phương trình 3x + 5y = -3.
Xét cặp số (0; 2) . Thay x = 0 ; y = 2 vào phương trình 3x + 5y = -3 ta được:
3x + 5y = 3.0 + 5.2 = 10 ≠ -3
⇒ (0; 2) không là nghiệm của phương trình 3x + 5y = -3.
Xét cặp (-1; 0).Thay x = -1 ; y = 0 vào phương trình 3x + 5y = -3 ta được:
3x + 5y = 3.(-1) + 5.0 = -3
⇒ (-1; 0) là nghiệm của phương trình 3x + 5y = -3. .
Xét cặp (1,5; 3). Thay x = 1,5 ; y = 3 vào phương trình 3x + 5y = -3 ta được:
3x + 5y = 3.1,5 + 5.3 = 4,5 + 15 = 19,5 ≠ -3
⇒ (1,5; 3) không là nghiệm của phương trình 3x + 5y = -3.
Xét cặp (4; -3). Thay x = 4 ; y = -3 vào phương trình 3x + 5y = -3 ta được:
3x + 5y = 3.4 + 5.(-3) = 12 – 15 = -3
⇒(4; -3) là nghiệm của phương trình 3x + 5y = -3.
Vậy có hai cặp số (-1; 0) và (4; -3) là nghiệm của phương trình 3x + 5y = -3.
Bài 2 Tìm hai nghiệm của phương trình x + y = 2 (1)
Lời giải:
+ Cho y = 0 ⇒ x = 2 → (2; 0) là một nghiệm của phương trình (1).
+ Cho y = 1 ⇒ x = 1 → (1; 1) là một nghiệm của phương trình (1).
⇒ (2; 0); (1; 1) là hai nghiệm cần tìm của phương trình x + y = 2.
Bài 3: Giải bài tập sau:
a,Kiểm tra xem các cặp số (1; 1) và (0,5; 0) có là nghiệm của phương trình 2x – y = 1 hay không ?
b) Tìm thêm một nghiệm khác của phương trình 2x – y = 1.
Giải:
a) Cặp số (1; 1) là nghiệm của phương trình 2x – y = 1 vì 2.1 – 1 = 1
Cặp số (0,5; 0) là nghiệm của phương trình 2x – y = 1 vì 2.0,5 – 0 = 1
b) Chọn x = 2 ta có: 2.2 – y = 1 ⇔ y = 3
Vậy cặp số (2; 3) là một nghiệm của phương trình 2x – y = 1
Dạng 2: Viết công thức nghiệm tổng quát của phương trình bậc nhất hai ẩn. Biểu diễn tập nghiệm trên hệ trục tọa độ.
Phương pháp: Xét phương trình bậc nhất hai ẩn ax+by=c
1. Để viết công thức nghiệm tổng quát của phương trình, trước tiên ta biểu diễn x theo y rồi đưa ra công thức nghiệm tổng quát.
2. Để biểu diễn tập nghiệm của phương trình trên mặt phẳng tọa độ, ta vẽ đường thẳng d có phương trình ax+by=c
Bài 1: Nêu nhận xét về số nghiệm của phương trình 2x – y = 1.
Giải:
Chọn x = x0 ( x0 ∈ R) ta có : 2×0 – y = 1 ⇔ y = 2×0 -1
Suy ra , mọi cặp số dạng (x0; 2×0 -1 )với x0 tùy ý đều là nghiệm của phương trình 2x – y = 1
Phương trình 2x – y = 1 có vô số nghiệm
Bài 2: Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:
a) 3x – y = 2;
b) x + 5y = 3;
c) 4x – 3y = -1;
d) x + 5y = 0 ;
e) 4x + 0y = -2 ;
f) 0x + 2y = 5.
Lời giải
a) 3x – y = 2 (1)
⇔ y = 3x – 2.
Vậy phương trình có nghiệm tổng quát là (x; 3x – 2) (x ∈ R).
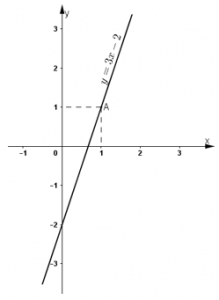
Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng y = 3x – 2 (Hình vẽ).
+ Tại x = 2/3 thì y = 0 ⇒ đường thẳng y = 3x – 2 đi qua điểm ( 2/3;0)
+ Tại x = 0 thì y = -2 ⇒ đường thẳng y = 3x – 2 đi qua điểm (0; -2).
Vậy đường thẳng y = 3x – 2 là đường thẳng đi qua điểm ( 2/3;0) và (0; -2).
c) x + 5y = 3 (2)
⇔ x = 3 – 5y
Vậy phương trình có nghiệm tổng quát là (3 – 5y; y) (y ∈ R).
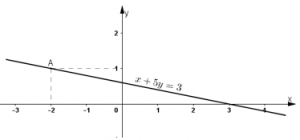
Đường thẳng biểu diễn tập nghiệm của (2) là đường thẳng x + 5y = 3.
+ Tại y = 0 thì x = 3 ⇒ Đường thẳng đi qua điểm (3; 0).
+ Tại x = 0 thì y=3/5 ⇒ Đường thẳng đi qua điểm (0;3/5)
Vậy đường thẳng x + 5y = 3 là đường thẳng đi qua hai điểm (3; 0) và (0;3/5)
c)4x – 3y = -1
⇔ 3y = 4x + 1
⇔
Vậy phương trình có nghiệm tổng quát là ( x; 4/3x + 1/3)
(x ∈ R).
Đường thẳng biểu diễn tập nghiệm phương trình là đường thẳng 4x – 3y = -1.
+ Tại x = 0 thì y = 1/3
Đường thẳng đi qua điểm (0;1/3)
+ Tại y = 0 thì x = -1/4
Đường thẳng đi qua điểm ( -1/4; 0)
Vậy đường thẳng 4x – 3y = -1 đi qua (0;1/3) và ( -1/4; 0)
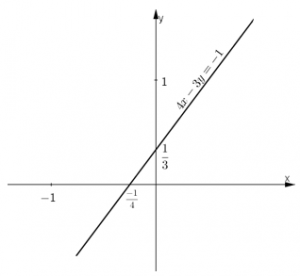
d)x + 5y = 0⇔ x = -5y.
Vậy nghiệm tổng quát của phương trình là (-5y; y) (y ∈ R).
Đường thẳng biểu diễn nghiệm của phương trình là đường thẳng x + 5y = 0.
+ Tại x = 0 thì y = 0 ⇒ Đường thẳng đi qua gốc tọa độ.
+ Tại x = 5 thì y = -1 ⇒ Đường thẳng đi qua điểm (5; -1).
Vậy đường thẳng x + 5y = 0 đi qua gốc tọa độ và điểm (5; -1).
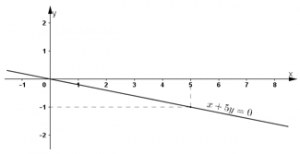
e) 4x + 0y = -2
⇔ 4x = -2 ⇔ x= 1/2
Phương trình có nghiệm tổng quát (-0,5; y)(y ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng x = -0,5 đi qua điểm (-0,5; 0) và song song với trục tung.
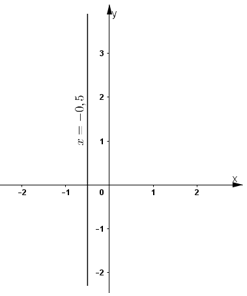
f) 0x + 2y = 5
⇔2y=5 ⇔ y=5/2
Phương trình có nghiệm tổng quát (x; 2,5) (x ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng y = 2,5 đi qua điểm (0; 2,5) và song song với trục hoành.
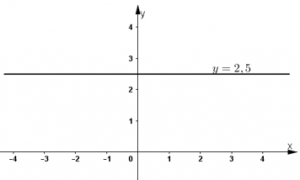
Dạng 3: Tìm điều kiện của tham số để đường thẳng ax + by = c thỏa mãn điều kiện cho trước
Phương pháp: Ta có thể sử dụng một số lưu ý sau đây khi giải dạng toán này:
1. Nếu a≠0 và b=0 thì phương trình đường thẳng d: ax + by = c có dạng d: x=c/a . Khi đó d sông song hoặc trùng với oy
2. nếu a=0 và b≠0 thì phương trình đường thẳng d: ax + by = c có dạng d: x=c/b . Khi đó d sông song hoặc trùng với ox
3. Đường thẳng d: ax + by = c đi qua M(x0;y0) khi và chỉ khi ax0 + by0 = c
Bài 1: Cho hai phương trình x + 2y = 4 và x – y = 1. Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và cho biết tọa độ của nó là nghiệm của các phương trình nào.
Lời giải:
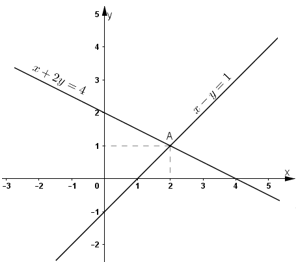
– Vẽ đường thẳng x + 2y = 4.
+ Với x = 0 ⇒ y = 2. Đường thẳng đi qua điểm (0; 2).
+ Với y = 0 ⇒ x = 4. Đường thẳng đi qua điểm (4; 0).
Đường x + 2y = 4 là đường thẳng đi qua điểm (0; 2) và (4; 0).
– Vẽ đường thẳng x – y = 1
+ Với x = 0 ⇒ y = -1. Đường thẳng đi qua điểm (0; -1).
+ Với y = 0 ⇒ x = 1. Đường thẳng đi qua điểm (1; 0).
Đường x – y = 1 là đường thẳng đi qua điểm (0 ; -1) và (1 ; 0).
– Giao điểm của hai đường thẳng là điểm A có tọa độ là (2; 1).
– Ta có A(2; 1) cùng thuộc hai đường thẳng nên nó là nghiệm của cả hai phương trình đã cho.
Bài 2: Cho phương trình 2x – 6 = 0. Đường thẳng biểu diễn tập nghiệm của phương trình trên là đường thẳng?
Giải:
Ta có: 2x – 6 = 0 ⇔ 2x = 6 ⇔ x = 3 Do đó, đường thẳng biểu diễn tập nghiệm phương trình đã cho là đường thẳng song song trục tung Oy.
Bài 3: Cho phương trình: 0x + √3y = 3. Đường thẳng biểu diễn tập nghiệm của phương trình trên là đường thẳng :
Giải:
Ta có:
0x + √3y = 3 ⇔ y = √3
Do đó, đường thẳng biểu diễn tập nghiệm của phương trình đã cho là đường thẳng song song trục hoành.
Dạng 4: Tìm các nghiệm nguyên của phương trình bậc nhất hai ẩn
Phương pháp: Để tìm các nghiệm nguyên của phương trình bậc nhất hai ẩn ax + by = c
Cách 1:
Bước 1: Rút gọn phương trình, chú ý đến tính chia hết của các ẩn
Bước 2: Biểu thị ẩn mà hệ số của nó có giá trị tuyệt đối nhỏ theo ẩn kia.
Bước 3: Tách riêng giá trị nguyên ở biểu thức của x
Bước 4: Đặt điều kiện để phân bố trong biểu thức của x bằng một số nguyên t, ta được một phương trình bậc nhất hai ẩn y và t
– Cứ tiếp tục như trên cho đến khi các ần đều được biểu thị dưới dạng một đa thức với các hệ số nguyên.
Cách 2:
Bước 1. Tìm một nghiệm nguyên (x0;y0)của phương trình.
Bước 2. Đưa phương trình về dạng a(x-x0) + b(y -y0) = 0 từ đó dễ dàng tìm được các nghiệm nguyên của phương trình đã cho.
Bài 1: Cho hai cặp số (1; 2) và (0; 1). Hỏi cặp nào là nghiệm của phương trình 2x + 3y = 8 ?
Lời giải:
+ Ta có 2.1 + 3.2 = 8 ⇒ (1; 2) là cặp nghiệm của phương trình 2x + 3y = 8.
+ Ta có 2.0 + 3.1 = 3 ≠ 8 ⇒ (0; 1) không phải là cặp nghiệm của phương trình 2x + 3y = 8
Bài 2: Cặp số (1:1) có phải là nghiệm của phương trình x + y = 1 không?
Lời giải:
Ta có: 1 + 1 = 2 ≠ 1 nên (1;1) không là nghiệm của phương trình x + y = 1
Bài 3: Cho phương trình (m – 2)x + (m – 1)y = 1 (m là tham số). Chứng minh rằng đường thẳng biểu diễn tập nghiệm của phương trình này luôn đi qua một điểm cố định với mọi giá trị của m
Lời giải:
Gọi (d) là đường thẳng biểu diễn tập nghiệm của phương trình
(m – 2)x + (M – 1)y = 1
Phương trình đường thẳng (d) chính là:
(m – 2)x + (M – 1)y = 1
Giả sử (d) luôn đi qua điểm M( x0; y0) với mọi m
Khi đó (m – 2)x + (M – 1)y = 1 với mọi m
⇔ (x0 + y0)m – (2x0 + y0 + 1) = 0 với mọi m
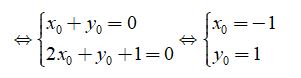
Vậy (d) luôn đi qua một điển cố định M(-1;1)
Bài 4: Tìm các điểm nằm trên đường thẳng 8x + 9y = -79 , có hoành độ và tung độ là các số nguyên và nằm trong góc vuông phần tư thứ III
Lời giải:
Ta cần tìm nghiệm nguyên của phương trình 8x + 9y = -79 , rút x từ phương trình ta được:
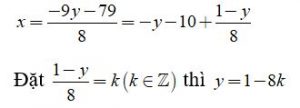
Từ đó ta được x= -(1 -8k) -10 +k = 9k -11
Vì điểm này nằm tròn góc phần tư thứ 3
Nên x<0 và y< 0
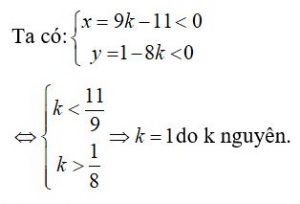
Với k=1 thì x= -2 và y= -7
Vậy có 1 điểm duy nhất phải tìm là (-2;-7)
Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình