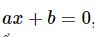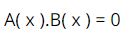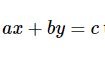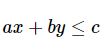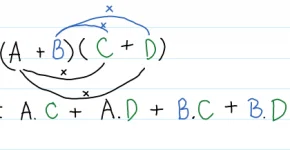Lý thuyết và cách giải bất phương trình bậc nhất một ẩn kèm theo bài tập
Bất phương trình chứa một ẩn rất quen thuộc đối với chương trình học của các bạn học sinh, sinh viên. Không chỉ trong Toán học, bất phương trình này còn rất cần thiết đối với nhiều môn học khác. Thông qua bài viết sau đây của chúng tôi, các bạn đọc sẽ được tìm hiểu về khái niệm bất phương trình bậc nhất một ẩn và tập nghiệm của bất phương trình.
Tham khảo thêm:
- Phân tích đa thức thành nhân tử chung và bài tập có lời giải từ A- Z
- Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp và bài tập có lời giải
- Rút gọn phân số là gì? Khái niệm rút gọn phân số và bài tập có lời giải chính xác 100%
Nội Dung
Bất phương trình bậc nhất một ẩn là gì ?
Bất phương trình một ẩn là bất phương trình có dạng ax + b < 0 ( hoặc ax + b > 0, ax + b ≤ 0, ax + b ≥ 0 ) trong đó a và b là hai số đã cho, a ≠ 0.
Quy tắc biến đổi bất phương trình
Quy tắc chuyển vế: Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.
Ví dụ: Giải bất phương trình x – 3 < 4.
Ta có x – 3 < 4
⇔ x < 4 + 3 (chuyển vế – 3 và đổi dấu thành 3)
⇔ x < 7.
Vậy tập nghiệm của bất phương trình là { x| x < 7 }.
Quy tắc nhân với một số: Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
- Giữ nguyên chiều bất phương trình nếu số đó dương.
- Đổi chiều bất phương trình nếu số đó âm.
Ví dụ: Giải bất phương trình (x – 1)/3 ≥ 2.
Ta có: (x – 1)/3 ≥ 2
⇔ (x – 1)/3.3 ≥ 2.3 (nhân cả hai vế với 3)
⇔ x – 1 ≥ 6 ⇔ x ≥ 7.
Vậy tập nghiệm của bất phương trình là { x| x ≥ 7 }.
Cách giải bất phương trình một ẩn
Áp dụng hai quy tắc biến đổi trên, ta giải bất phương trình bậc nhất một ẩn như sau:
Dạng ax + b > 0 ⇔ ax > – b
⇔ x > – b/a nếu a > 0 hoặc x < – b/a nếu a < 0.
Vậy bất phương trình có tập nghiệm là
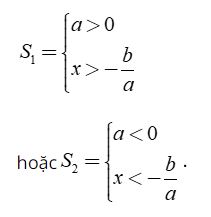
Các dạng toán như ax + b < 0, ax + b ≤ 0, ax + b ≥ 0 tương tự như trên
Các dạng bài tập thường gặp ở bất phương trình bậc nhất một ẩn
Bài 1: Tìm tập nghiệm của các bất phương trình sau:
a) ( x + √ 3 )2 ≥ ( x – √ 3 )2 + 2
b) x + √ x < ( 2√ x + 3 )( √ x – 1 )
c) (x – 3)√(x – 2) ≥ 0
Lời giải:
a) Ta có: ( x + √ 3 )2 ≥ ( x – √ 3 )2 + 2
⇔ x2 + 2√ 3 x + 3 ≥ x2 – 2√ 3 x + 3 + 2
⇔ 4√3x ≥ 2 ⇔ x ≥ √3/6
Vậy bất phương trình đã cho có tập nghiệm là S = [ √ 3 /6; + ∞ )
b) Ta có: x + √ x < ( 2√ x + 3 )( √ x – 1 )
Điều kiện: x ≥ 0
⇔ x + √ x < 2x – 2√ x + 3√ x – 3
⇔ – x < – 3 ⇔ x > 3
Kết hợp điều kiện, tập nghiệm bất phương trình là: x > 3
Vậy bất phương trình đã cho có tập nghiệm là x > 3
c) Ta có: (x – 3)√(x – 2) ≥ 0
Điều kiện: x ≥ 2
Bất phương trình tương đương là:
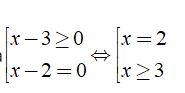
Bài 2: Có bao nhiêu giá trị thực của tham số m để bất phương trình ( m2 – m )x < m vô nghiệm là?
Lời giải:
Rõ ràng nếu m2 – m ≠ 0 ⇔ m ≠ 0; m ≠ 1 thì bất phương trình luôn có nghiệm.
Với m = 0, bất phương trình trở thành 0x < 0: vô nghiệm.
Với m = 1, bất phương trình trở thành 0x < 1: luôn đúng với mọi x ∈ R
Vậy với m = 0 thì bất phương trình trên vô nghiệm.
Bài 3: Lập bất phương trình cho bài toán sau:
Cô Lan chia đều 20 cái kẹo cho 4 bạn nhỏ. Hỏi mỗi bạn được bao nhiêu cái kẹo để sau khi chia xong cô Lan vẫn còn kẹo?
Lời giải:
Gọi số kẹo mỗi bạn nhận được là x ( cái kẹo)
Khi đó, 4 bạn sẽ có tất cả: 4x ( cái kẹo)
Để sau khi chia xong, cô Lan vẫn còn kẹo thì 4x < 20
Baì 4: Giải bất phương trình:
a,Ta có: 8x + 4 > 2( x +5 )
⇔ 8x + 4 > 2x + 10
⇔ 8x – 2x > 10 – 4
⇔ 6x > 6
⇔ x > 6 : 6
⇔ x > 1
b, Ta có: 2(x + 2)2 < 2x(x + 2) + 4
⇔ 2x2 + 8x + 8 < 2x2 + 4x + 4
⇔ 4x < -4
⇔ x < -1.
c, Ta có: (x + 3)(x + 4) > (x – 2)(x + 9) + 25
⇔ x2 + 7x + 12 > x2 + 7x – 18 + 25
⇔ x2 + 7x + 12 – x2 – 7x + 18 – 25 > 0
⇔ x > 0
d, Ta có: 5x – 1 ≥ (2x)/5 + 3
⇔ 25x – 5 ≥ 2x + 15
⇔ 23x ≥ 20
⇔ x ≥ 20/23.
Bài 5: Tìm m để x = 2 là nghiệm bất phương trình: mx + 2 < x + 3 + m
Lời giải:
Do x = 2 là nghiệm của bất phương trình đã cho nên:
⇔ 2m + 2 < 2 + 3 + m
⇔ 2m – m < 2 + 3- 2
⇔ m < 3
Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình