Bảng nguyên hàm, công thức nguyên hàm kèm VD có lời giải

Bảng nguyên hàm là một dạng toán giải tích rất quan trọng đối với học sinh THPT, dang toán này chúng ta bắt gặp rất nhiều và đã có rất nhiều bài toán trong các kỳ thi đại học có dàng toán này.

Hôm nay THPT Chuyên Lam Sơn xin gửi đến các bạn công thức nguyên hàm thường gặp đầy đủ nhất với các dạng : Nguyên hàm căn x, 1/x, nguyên hàm a mũ x, nguyên hàm căn u , nguyên hàm sin , nguyên hàm logarit , nguyên hàm 1/u …

1. Định nghĩa về nguyên hàm cơ bản

Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.

Kí hiệu: ∫ f(x)dx = F(x) + C.

Định lí 1:

1) Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.

2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.

Do đó F(x) + C; C ∈ R là họ tất cả các nguyên hàm của f(x) trên K.

Tính chất của nguyên hàm

• (∫ f(x)dx)’ = f(x) và ∫ f'(x)dx = f(x) + C.
• Nếu F(x) có đạo hàm thì: ∫d(F(x)) = F(x) + C).
• ∫ kf(x)dx = k∫ f(x)dx với k là hằng số khác 0.
• ∫[f(x) ± g(x)]dx = ∫ f(x)dx ± ∫g(x)dx.

2. Công thức bảng nguyên hàm cơ bản 

Tham khảo thêm: Công Thức Đạo Hàm Log, căn bậc 3 , căn u, căn x, căn logarit

3. Bảng nguyên hàm nâng cao ( a≠0 )

Xem ngay: Hệ Thức Lượng Trong Tam Giác Vuông, Cân, Thường Lớp 8, 9, lớp 10

4. Bảng nguyên hàm mở rộng ( a≠0)

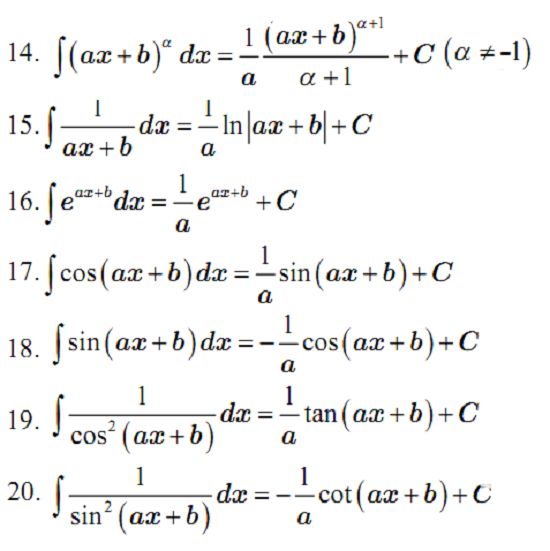
Để học tốt được phần này các bạn cần nắm rõ kiến thức về đạo hàm, vi phân. Cần phải biết phân biệt đạo hàm của các hàm sơ cấp, đạo hàm của hàm hợp.

Đa số khi giải dạng đề này các bạn thường mắc phải các sai lầm như:

• Hiểu sai bản chất công thức
• Cẩu thả, dẫn đến tính sai nguyên hàm
• Không nắm vững định nghĩa về nguyên hàm, tích phân
• Đổi biến số nhưng quên đổi cận
• Đổi biến không tính vi phân
• Không nắm vững phương pháp nguyên hàm từng phần

Một số phương pháp tìm nguyên hàm thường gặp

1. Phương pháp đổi biến

1.1. Đổi biến dạng 1

a. Định nghĩa.

Cho hàm số u = u(x) có đạo hàm liên tục trên K và hàm số y = f(u) liên tục sao cho f[u(x)] xác định trên K. Khi đó, nếu F là một nguyên hàm của f, tức là: ∫ f(u)du = F(u) + C thì:

∫ f[u(x)]u'(x)dx = F[u(x)] + C

b. Phương pháp giải

• Bước 1: Chọn t = φ(x). Trong đó φ(x) là hàm số mà ta chọn thích hợp.
• Bước 2: Tính vi phân hai vế: dt = φ'(t)dt.
• Bước 3: Biểu thị: f(x)dx = f[φ(t)]φ'(t)dt = g(t)dt.
• Bước 4: Khi đó: I = ∫ f(x)dx = ∫g(t)dt = G(t) + C.

Ví dụ: Cho hàm số u = u(x) có đạo hàm liên tục trên K, y = f(u) liên tục để f[u(x)] xác định trên K và ∫f(u)du = F(u) + C thì:

∫f[u(x)]u'(x)dx = F[u(x)] + C

1.2. Phương pháp đổi biến loại 2

a. Định nghĩa:

Cho hàm số f(x) liên tục trên K; x = φ(t) là một hàm số xác định, liên tục trên K và có đạo hàm là φ'(t). Khi đó, ta có:

∫ f(x)dx = ∫ f[φ(t)].φ'(t)dt

b. Phương pháp chung

• Bước 1: Chọn x = φ( t), trong đó φ(t) là hàm số mà ta chọn thích hợp.
• Bước 2: Lấy vi phân hai vế: dx = φ'(t)dt.
• Bước 3: Biến đổi: f(x)dx = f[φ(t)]φ'(t)dt = g(t)dt.
• Bước 4: Khi đó tính: ∫ f(x)dx = ∫g(t)dt = G(t) + C.

c. Các dấu hiệu đổi biến thường gặp

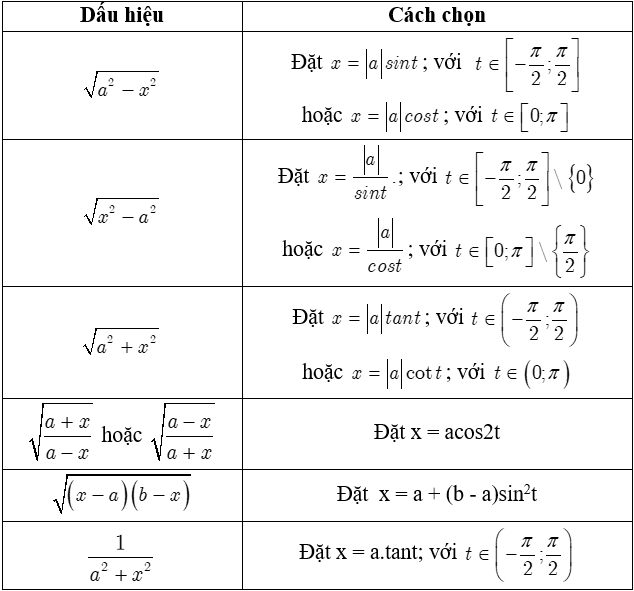
2. Phương pháp nguyên hàm từng phần

a. Định lí

Nếu u(x), v(x) là hai hàm số có đạo hàm liên tục trên K:

∫u(x).v'(x)dx = u(x).v(x) – ∫v(x).u'(x)dx

Hay ∫udv = uv – ∫vdu

(với du = u'(x)dx, dv = v'(x)dx)

b. Phương pháp chung

Bước 1: Ta biến đổi tích phân ban đầu về dạng: I = ∫ f(x)dx = ∫ f1(x).f2(x)dx

Bước 2: Đặt: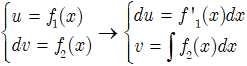

Bước 3: Khi đó: ∫u.dv = u.v – ∫v.du

Bài 1: Tìm nguyên hàm của hàm số

Bài 2: Tìm nguyên hàm của hàm số

Sau khi đọc xong bài viết của chúng tôi có thể giúp các bạn nhớ được bảng nguyên hàm và công thức nguyên hàm để áp dụng vào làm bài tập đơn giản mà chính xác hơn nhé