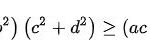7 Hằng Đẳng Thức Đáng Nhớ lớp 8 Chi Tiết, Đầy Đủ, Chính Xác
7 hằng đẳng thức đáng nhớ là những hằng đẳng thức không còn xa lạ với các bạn nữa, Hôm nay THPT CHUYÊN LAM SƠN sẽ nói kỹ hơn về 7 hằng đẳng thức quan trọng là: bình phương của một tổng, bình phương của một hiệu, hiệu của hai bình phương, lập phương của một tổng, lập phương của một hiệu, tổng hai lập phương và cuối cùng là hiệu hai lập phương kèm theo các dạng bài tập có lời giải chi tiết để các bạn cùng tham khảo.
Nội Dung
Chi tiết 7 hằng đẳng thức đáng nhớ
- ( A + B )² = A² + 2AB + B² (1)
- ( A – B )² = A² – 2AB + B² (2)
- A² – B² = ( A – B )( A + B ) (3)
- ( A + B )³ = A³ + 3A²B + 3AB² + B³ (4)
- ( A – B )³ = A³ – 3A²B + 3AB² – B³ (5)
- A³ + B³ = ( A + B )( A² – AB + B² ) (6)
- A³ – B³ = ( A – B )( A² + AB + B² ) (7)
1. Bình phương của một tổng
Bình phương của một tổng sẽ bằng bình phương của số thứ nhất cộng hai lần tích của số thứ nhất và số thứ hai, sau đó cộng với bình phương của số thứ hai.
(a+b)² = a² + 2ab +b²
Ví dụ:
a) Tính (x + 1)³.
b) Tính (2x + y)³.
Lời giải
a) Ta có:
(x + 1)³ = x³ + 3.x².1 + 3.x.1² + 1³
= x³ + 3x² + 3x + 1.
Vậy (x + 1)³ = x3 + 3x² + 3x + 1.
b) Ta có:(2x + y)³ = (2x)³ + 3.(2x)².y + 3.2x.y² + y³
= 8x³ + 3.4x².y + 6xy² + y³
= 8x³ + 12x²y + 6xy² + y³.
Vậy (2x + y)³ = 8x³ + 12x²y + 6xy² + y³.
2. Bình phương của một hiệu
Bình phương của một hiệu sẽ bằng bình phương của số thứ nhất trừ đi hai lần tích của số thứ nhất và số thứ hai, sau đó cộng với bình phương của số thứ hai.
(a-b)² = a² – 2ab +b²
Ví dụ: Tính (5x-y)²
Lời giải
Ta có: (5x-y)² = (5x)² – 2.5x.y + (y)²
= 25x² -10xy + y²
Tham khảo thêm: Định Lý và Công thức Sin Cos Tan lớp 9, lớp 10, lớp 11, lớp 12
3. Hiệu hai bình phương
Hiệu của hai bình phương của hai số sẽ bằng hiệu của hai số đó nhân với tổng của hai số đó.
a² – b² = (a – b)(a +b)
Ví dụ: m² – 4 = m² – 2² = (m – 2)(m + 2)
(2a – b)(2a + b) = (2a)² – b² = 4a² – b²
Ví dụ 2: Khai triển các hằng đẳng thức sau:
a. (xy -1)²
b.(a-4)(a+4)
Lời giải
a) (xy – 1)² = (xy)² – 2xy.1 + 1² = x²y² – 2xy + 1.
b) (a – 4)(a + 4) = a² – 4² = a² – 16.
4. Lập phương của một tổng
Lập phương của một tổng của hai số sẽ bằng lập phương của số thứ nhất cộng với ba lần tích của bình phương số thứ nhất nhân cho số thứ hai, cộng với ba lần tích của số thứ nhất nhân với bình phương của số thứ hai, rồi sau đó cộng với lập phương của số thứ hai.
( A + B )³ = A³ + 3A²B + 3AB² + B³
Ví dụ: Tính:
a) (2x² + 3y)³;
b) (½x−3)³.
Lời giải
a) Ta thấy rằng biểu thức này có dạng vế trái của hằng đẳng thức số (4) với A = 2x², B = 3y.
Áp dụng hằng đẳng thức số (4), ta có:
(2x² + 3y)3 = (2x²)3 + 3.(2x²)².3y + 3.2x².(3y)² + (3y)³
= 8x6 + 3.4x4.3y + 3.2x².9y² + 27y³
= 8x6 + 36x4y + 54x²y² + 27y³
Vậy (2x² + 3y)³ = 8x6 + 36x4y + 54x²y² + 27y³.
b) Ta thấy rằng biểu thức này có dạng vế trái của hằng đẳng thức số (5) với A = ½x và B = 3
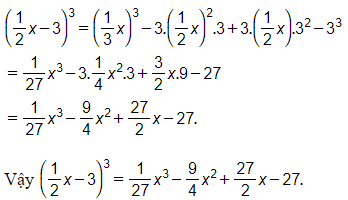
Xem ngay: Công Thức Đạo Hàm Log, căn bậc 3 , căn u, căn x, căn logarit
5. Lập phương của một hiệu
Lập phương của một hiệu của hai số sẽ bằng lập phương của số thứ nhất trừ đi ba lần tích của bình phương số thứ nhất nhân cho số thứ hai, cộng với ba lần tích của số thứ nhất nhân với bình phương của số thứ hai, rồi sau đó trừ đi lập phương của số thứ hai.
( A – B )³ = A³ – 3A²B + 3AB² – B³
Ví dụ 1: Viết các biểu thức sau dưới dạng lập phương của một hiệu
8 – 12x + 6x² – x³
= 2³ – 3.2².x + 3.2.x² – x³
= (2 – x)³
Ví dụ 2: Tính (2x – 3y)³
Lời giải
Ta có:
(2x – 3y)³ = (2x)³ – 3.(2x)².3y + 3.2x.(3y)² – (3y)³
= 8x³ – 36x²y + 54xy² – 27y³
6. Tổng hai lập phương
Tổng của hai lập phương của hai số sẽ bằng tổng của số thứ nhất cộng với số thứ hai, sau đó nhân với bình phương thiếu của tổng số thứ nhất và số thứ hai.
A³ + B³ = ( A + B )( A² – AB + B² )
Ví dụ: x³ + 4³ = (x + 4)(x² – 4x + 4²) = (x + 4)(x² – 4x + 16)
¹⁄27 +u³ = (¹⁄3)³ + u³
= (¹⁄3+u)[(¹⁄3)²−¹⁄3u + u²]
= (¹⁄3+u)(¹⁄9 − u³/3 + u²)²
Ví dụ 2: Viết biểu thức (x² + 3)(x4 – 3x² + 9) dưới dạng tổng hai lập phương
Ta có (x² + 3)(x4 – 3x² + 9)
= (x² + 3)((x²)² – 3.x² + 3²)
= (x²)³ + 3³
7. Hiệu hai lập phương
Hiệu của hai lập phương của hai số sẽ bằng hiệu của số thứ nhất trừ đi số thứ hai, sau đó nhân với bình phương thiếu của tổng số thứ nhất và số thứ hai.
A³ – B³ = ( A – B )( A² + AB + B² )
Ví dụ 1: Viết biểu thức (3x – 4)(9x² + 12x + 16) dưới dạng hiệu hai lập phương
Ta có (3x – 4)(9x² + 12x + 16)
= (3x – 4)((3x)² + 3x.4 + 4²)
= (3x)³ – 4³
Ví dụ 2:
x³ – (2y)³ = (x – 2y)[x² + 2xy + (2y)²] = (x – 2y)(x² + 2xy + 4y²)
Hằng đẳng thức mở rộng
Hằng đẳng thức đáng nhớ hàm bậc 2
- (a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc
- (a + b − c)² = a² + b² + c² + 2ab − 2ac − 2bc
- (a − b − c)² = a² + b² + c² − 2ab − 2ac + 2bc
Hằng đẳng thức đáng nhớ hàm bậc 3
- a³ + b³ = (a + b)³ – 3ab(a + b)
- a³ – b³ = (a – b)³+ 3ab(a – b)
- (a + b +c)³ = a³ + b³ + c³ + 3(a + b)(a + c)(b + c)
- a³ + b³ + c³ − 3abc = (a + b + c)(a² + b² + c² − ab − bc − ca)
- (a – b)³+(b – c)³+(c – a)³ = 3(a – b)(b – c)(c – a)
- (a + b)(b + c )(c + a) – 8abc = a(b – c)² + b(c – a)² + c(a – b)²
- (a + b)(b + c)(c + a) = (a + b + c)(ab + bc + ca) − abc
- (a + b)(b + c)(c + a) – 8abc = a(b – c)² + b(c – a)² + c(a – b)²
- (a + b)(b + c)(c + a) = (a + b + c)(ab + bc + ca) – abc
Hằng đẳng thức dạng tổng quát
an+bn=(a+b)(an−1−an−2b+an−3b2−an−4b3+…+a2bn−3−a.bn−2+bn−1)
Với n là số lẻ thuộc tập N
an–bn=(a–b)(an–1+an–2b+an–3b2+…+a2bn–3+abn–2+bn–1)
Tham khảo thêm: Bảng nguyên hàm, công thức nguyên hàm kèm VD có lời giải
Các dạng bài tập áp dụng 7 hằng đẳng thức đáng nhớ
Dạng 1 : Tính giá trị của biểu thức
Phương pháp giải: Sử dụng trực tiếp các hằng đẳng thức đã học để khai triển các biểu thức
Ví dụ: Tính giá trị của biểu thức : A = x² – 4x + 4 tại x = -1
* Lời giải.
– Ta có : A = x² – 4x + 4 = x² – 2.x.2 + 2² = (x – 2)²
– Tại x = -1 : A = ((-1) – 2)² = (-3)²= 9
⇒ Kết luận: Vậy tại x = -1 thì A = 9
Ví dụ 2: Viết các biểu thức sau dưới dạng bình phương một tổng hoặc bình phương một hiệu:
a, 4x² + 4x + 1
b, x² – 8x + 16
Lời giải
a, 4x² + 4x + 1
= (2x)² + 2.2x.1 + 1²
= (2x + 1)²
b, x²– 8x + 16
= x² – 2.x.4 + 4²
= (x – 4)²
Dạng 2 : Chứng minh biểu thức A không phụ thuộc vào biến
Phương pháp: Để chứng minh 1 một biểu thức không phụ thuộc vào biến ta cần:
- Thực hiện phép nhân đơn thức với đa thức, đa thức với đa thức ( Nếu có)
- Nhóm các đơn thức đồng dạng với nhau rồi rút gọn.
Ví dụ 1: Chứng minh biểu thức sau không phụ thuộc vào x: A = (x – 1)² + (x + 1)(3 – x)
Lời giải.
Ta có: A =(x – 1)² + (x + 1)(3 – x) = x² – 2x + 1 – x² + 3x + 3 – x = 4 hằng số không phụ thuộc vào biến x.
Ví dụ 2: Chứng minh biểu thức sau không phụ thuộc vào giá trị của biến
B = x² (x – 2) – x(x² + x + 1) + x(3x + 1)
Lời giải
Ta có:
B = x² (x – 2) – x(x² + x + 1) + x(3x + 1)
= x² .x – x² .2 – x.x² – x.x – x.1 + x.3x + x.1
= x³ – 2x² – x³ – x² – x + 3x² + x
= (x³ – x³) + (3x² – 2x² – x² ) + (x – x)
= 0 + 0 + 0
= 0
Vậy giá trị của biểu thức B không phụ thuộc vào x.
Ví dụ 3: Chứng minh biểu thức sau không phụ thuộc vào giá trị của x và y
A = (x – y).(x + y) + (y – x).(y + x) + 10
Lời giải
Ta có:
A = (x – y).(x + y) + (y – x).(y + x) + 10
= x(x + y) – y(x + y) + y.(y + x) – x(y + x) + 10
= x² + xy – xy – y² + y² + xy – xy – x² + 10
= (x² – x²) + (y² – y²) + (xy – xy + xy – xy) + 10
= 0 + 0 + 0 + 10
= 10
Vậy giá trị của biểu thức A là 10 và không phụ thuộc vào x và y.
Dạng 3 : Tìm giá trị nhỏ nhất của biểu thức
Phương pháp: Để tìm giá trị nhỏ nhất của A, ta cần:
- Chứng minh A ≥ k với k là hằng số
- Chỉ ra dấu “=” có thể xảy ra với giá trị nào đó của biến
Ví dụ 1: Tính giá trị nhỏ nhất của biểu thức: A = x² – 2x + 5
Lời giải:
Ta có : A = x² – 2x + 5 = (x² – 2x + 1) + 4 = (x – 1)2 + 4
Vì (x – 1)² ≥ 0 với mọi x.
⇒ (x – 1)2² + 4 ≥ 4 hay A ≥ 4
– Vậy giá trị nhỏ nhất của A = 4, Dấu “=” xảy ra khi : x – 1 = 0 hay x = 1
⇒ Kết luận GTNN của A là: Amin = 4 ⇔ x = 1
Ví dụ 2: Tìm giá trị nhỏ nhất của biểu thức C = 4x² + 8x + 10
Lời giải
C = 4x² + 8x + 10 = (2x)² + 2.2x.2 + 4 + 6
= (2x + 2)² + 6
Với mọi x ta có: (2x + 2)² ≥ 0 ⇒ (2x + 2)² + 6 ≥ 6
Do đó, giá trị nhỏ nhất của biểu thức C là 6
Ví dụ 3:Tìm giá trị nhỏ nhất của A = 2x² – 8x + 1
Lời giải
a, A = 2(x² – 4x + 4) – 7 = 2(x – 2)² – 7 ≥ -7
min A = -7 khi và chỉ khi x = 2
Dạng 4 : Tìm giá trị lớn nhất của biểu thức
Phương pháp: Để tìm giá trị lớn nhất của A, ta cần:
- Chứng minh A ≤ k với k là hằng số
- Chỉ ra dấu “=” có thể xảy ra với giá trị nào đó của biến
Ví dụ: Tính giá trị lớn nhất của biểu thức: A = 4x – x²
Lời giải:
Ta có : A = 4x – x² = 4 – 4 + 4x – x² = 4 – (4 – 4x + x²) = 4 – (x² – 4x + 4) = 4 – (x – 2)²
Vì (x – 2)² ≥ 0 với mọi x ⇔ -(x – 2)² ≤ 0 với mọi x
⇔ 4 – (x – 2)² ≤ 4 [cộng 2 vế với 4]
⇔ A ≤ 4 Dấu “=” xảy ra khi : x – 2 = 0 hay x = 2
⇒ Kết luận GTLN của A là: Amax = 4 ⇔ x = 2.
Ví dụ 2: Tìm giá trị lớn nhất của B = -5x² – 4x + 1
Lời giải
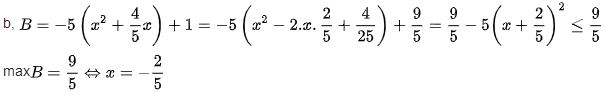
Dạng 5 : Chứng minh đẳng thức bằng nhau
Phương pháp giải: Áp dụng phép nhân đơn thức với đơn thức, nhân đa thức với đơn thức và nhân đa thức với đa thức với đa thức. Chúng ta biến đổi:
- Cách 1: Vế trái và chứng minh bằng vế phải
- Cách 2: Vế phải và chứng minh bằng vế trái
- Cách 3: Vế trái và vế phải cùng bằng một biểu thức.
Ví dụ 1: Chứng minh đẳng thức sau đúng: (a + b)³ – (a – b)³ = 2b(3a² + b²)
Lời giải:
Đối với dạng toán này chúng ta biến đổi VT = VP hoặc VT = A và VP = A
Ta có: VT = (a + b)³ – (a – b)³
= (a³ + 3a²b + 3ab² + b³) – (a³ – 3a²b + 3ab² – b³)
= a³ + 3a²b + 3ab² + b³ – a³ + 3a²b – 3ab² + b³
= 6a²b + 2b³
= 2b(3a² + b²) = VP (đpcm).
⇒ Kết luận, vậy : (a + b)³ – (a – b)³ = 2b(3a² + b²)
Ví dụ 2. Chứng minh 2x + y + y² = (1 – xy + y).(2x + y) + xy(2x + y – 2)
Chứng minh.
Ta có VP = (1 – xy + y).(2x + y) + xy(2x + y -2)
= 2x + y – 2x²y – xy² + 2xy + y² + 2x²y + xy² – 2xy
= 2x + y + y² = VT
Ví dụ 3: Chứng minh x(x + y²) – y(x – y) = ( -xy + x² + y²)(x + 1) – x²(x + y)
Lời giải
VP = (-xy + x² + y²)(x + 1) – x²(x – y)
= -x²y – xy + x³ + x² + xy² + y² – x3 + x²y
= (-x²y + x²y) + (x³ – x³) + x² + y² + xy² – xy
= x² + y² + xy² – xy (1)
VT = x(x + y²) – y(x – y)
= x² + xy² – xy + y² (2)
Từ (1) và (2) suy ra: x(x + y²) – y(x – y) = (-xy + x² + y²)(x + 1) – x²(x + y)
Dạng 6: Chứng minh bất đẳng thức
Phương pháp: Biến đổi bất đẳng thức về dạng biểu thức A ≥ 0 hoặc A ≤ 0. Sau đó dùng các phép biến đổi đưa A về 1 trong 7 hằng đẳng thức.
Ví dụ 1: Chứng minh rằng: (a+b)² ≥ 4ab
Lời giải
Giả sử (a+b)² < 4ab
⇒ a² + 2ab + b² < 4ab
⇒ a² + 2ab + b² – 4ab < 0
⇒ (a+b)² < 0
Điều này là vô lý với mọi a và b
Vậy điều giả sử là sai suy ra điều phải chứng minh.
Ví dụ 2:

Dấu “=” xảy ra ⇔ ax = bx
Áp dụng:
Ta viết bất đẳng thức
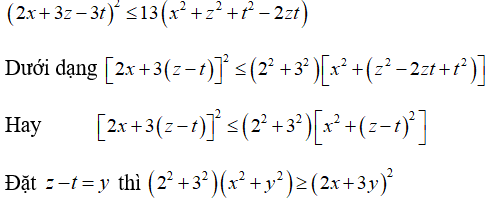
đúng theo bất đẳng thức vừa chứng minh ở trên.
Dạng 7: Phân tích đa thức thành nhân tử
Phương pháp đặt nhân tử chung
Khi tất cả các số hạng của đa thức có một thừa số chung, ta đặt thừa số chung đó ra ngoài dấu ngoặc () để làm nhân tử chung.
Các số hạng bên trong dấu () có được bằng cách lấy số hạng của đa thức chia cho nhân tử chung.
Chú ý: Nhiều khi để làm xuất hiện nhân tử chung ta cần đổi dấu các hạng tử.
( lưu ý tính chất: A = -(-A)).
Ví dụ 1: Phân tích đa thức sau thành nhân tử: A = x² – 4x + 4 – y²
Lời giải:
Ta có : A = x² – 4x + 4 – y² [để ý x² – 4x + 4 có dạng hằng đẳng thức]
= (x² – 4x + 4) – y² [nhóm hạng tử]
= (x – 2)² – y² [xuất hiện đẳng thức số A² – B²]
= (x – 2 – y )( x – 2 + y)
⇒ A = (x – 2 – y )( x – 2 + y)
Ví dụ 2: Phân tích các đa thức sau thành nhân tử
a, ( ab – 1 )² + ( a + b )²
b, x³ + 2x² + 2x + 1
c, x² – 2x – 4y² – 4y
Lời giải
a) Ta có ( ab – 1 )² + ( a + b )² = a²b² – 2ab + 1 + a² + 2ab + b²
= a²b² + a² + b² + 1 = ( a²b² + a² ) + ( b² + 1 )
= a²( b² + 1 ) + ( b² + 1 ) = ( a² + 1 )( b² + 1 )
b) Ta có x³ + 2x² + 2x + 1 = ( x³ + 1 ) + ( 2x² + 2x )
= ( x + 1 )( x² – x + 1 ) + 2x( x + 1 ) = ( x + 1 )( x² + x + 1 )
c) Ta có x² – 2x – 4y² – 4y = ( x² – 4y² ) – ( 2x + 4y )
= ( x – 2y )( x + 2y ) – 2( x + 2y )
= ( x + 2y )( x – 2y – 2 ).
Dạng 8: Tìm giá trị của x để biểu thức có giá trị thỏa mãn đẳng thức, bất đẳng thức
Phương pháp giải
a) Tìm điều kiện của x để biểu thức A < m (hoặc A > m ; A ≥ m; A ≤ m)
- Tìm đkxđ
- Rút gọn biểu thức (nếu cần)
- Biến đổi điều kiện A < m để tìm ra x.
Lưu ý: Khi nhân (chia) cả 2 vế của BPT với một biểu thức dương thì chiều của BPT không đổi.
b) Tìm điều kiện của x để hàm số đạt GTLN, GTNN.
- Tìm đkxđ
- Rút gọn biểu thức (nếu cần).
- Áp dụng các bất đẳng thức dể đánh giá biểu thức ≤ k (tìm GTLN) hoặc ≥ k (tìm GTNN) (k là hằng số)
- Tìm x để dấu = xảy ra.
Lưu ý: Bất đẳng thức Cô-si: a² + b² ≥ 2ab
A² ≥ 0 với mọi A
Ví dụ: Tìm giá trị củ x biết: x²( x – 3) – 4x + 12 = 0
Lời giải.
x² (x – 3) – 4x + 12 = 0
⇔ x² (x – 3) – 4(x – 3) = 0
⇔ (x – 3) (x² – 4) = 0
⇔ (x – 3)(x – 2)(x + 2) = 0
⇔ (x – 3) = 0 hoặc (x – 2) = 0 hoặc (x + 2) = 0
⇔ x = 3 hoặc x = 2 hoặc x = –2
⇒ Kết luận, vậy nghiệm : x = 3; x = 2; x = –2
Sau khi đọc xong bài viết của chúng tôi có thể giúp các bạn nhớ được 7 hằng đẳng thức đáng nhớ lớp 8 để áp dụng vào làm bài tập rồi nhé. Hãy thường xuyên theo dõi chúng tôi để được chia sẻ những kiến thức bổ ích khác về môn hóa, lý, văn,..