Công Thức Tính Thể Tích Khối Nón Tròn Xoay, Cụt kèm VD

Bạn đang có bài toán về thể tích khối nón nhưng bạn lại không nhớ công thức tính thể tích khối nón như thế nào để áp dụng vào làm bài tập. Chính vì vậy, THPT Chuyên Lam Sơn sẽ chia sẻ công thức tính thế tích khối nón cụt và khối nón tròn xoay kèm theo các dạng bài tập có lời giải chi tiết để các bạn cùng tham khảo nhé.

Nội Dung

Công thức tính thể tích khối nón

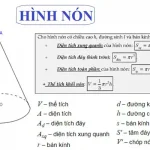
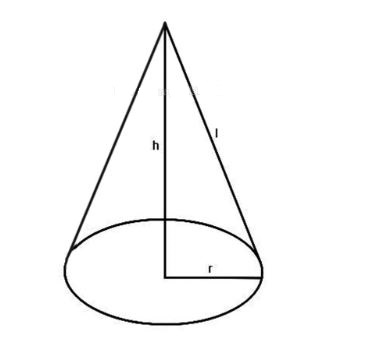
Thể tích khối nón được tính bằng 1/3 tích của số pi nhân với bình phương bán kính đáy mặt món và nhân với chiều cao của hình nón

V = 1/3.π.R².h

Trong đó:

V là thể tích của một hình nón bất kỳ
R là bán kính mặt đáy
H là đường cao hình nón
π = 3,14

Tham khảo thêm: Công thức tính diện tích, thể tích hình trụ kèm VD minh họa

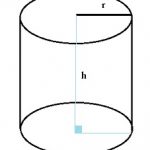
Công thức tính thể tích khối nón tròn xoay

Thể tích khối nón tròn xoay bằng tích diện tích mặt đáy của hình nón và chiều cao của hình nón

V = 1/3.B.h = 1/3.π.R².h

Trong đó:

V là thể tích của một hình nón bất kỳ
B là diện tích mặt đáy của hình nón
h là chiều cao hình nón

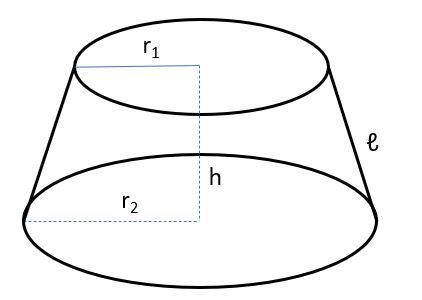
Công thức tính thể tích khối nón cụt

V = 1/3.π.(r₁² + r₂² + r₁.r₂).h

Trong đó:

V là thể tích hình nón cụt.
r₁ và r₂ là bán kính 2 đáy của hình nón cụt.
h là chiều cao của hình nón cụt (khoảng cách giữa 2 đáy).

Bài tập tính thể tích khối nón tròn xoay, cụt có lời giải

Ví dụ 1: Cho hình nón cụt có đường kính hai mặt đáy lần lượt là 12 cm và 16 cm. Chiều cao nối giữa hai mặt đáy dài 7 cm. Tính thể tích hình nón cụt.

Giải

Đường kính hai mặt đáy lần lượt là 12 cm và 18 cm.

Vậy bán kính đáy r₁ = 12/2 = 6cm; r₂ = 18/2 = 9cm; h = 7cm

V = 1/3.π.(r₁² + r₂² + r₁.r₂).h = 1/3π(6² + 9² +6.9).7 = 1253,5cm³

Vậy thể tích hình nón cụt xấp xỉ 1253,5cm³

Ví dụ 2: Một khối nón có thể tích bằng 30 π, nếu giữ nguyên chiều cao và tăng bán kính khối nón đó lên 2 lần thì thể tích của khối nón mới bằng bao nhiêu?

Lời giải

Gọi V₁ = 1/3.π.R².h là thể tích của khối nón ban đầu

⇒ Thể tích của khối nón lúc sau là:

V₂ = 1/3.π(2R)².h = 4/3πR².h = 4V₁ = 4.30π = 120π

Ví dụ 3: Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng a√2. Tính thể tích khối nón.

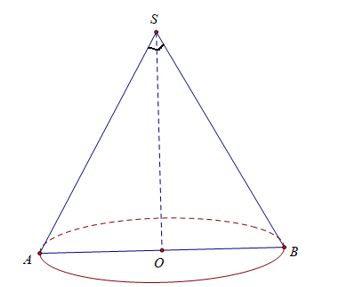
Lời giải

Thiết diện thu được khi cắt hình nón bằng mặt phẳng đi qua trục là tam giác SAB

⇒ ∆SAB vuông cân tại S, có AB = a√2

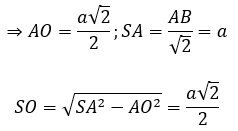
Thể tích khối nón là:

V = 1/3.π(2R)².h

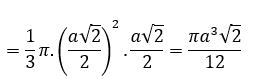
Ví dụ 4: Một hình nón có đường kính đáy là 2a√3 , góc ở đỉnh là 120⁰. Tính thể tích của khối nón đó theo a.

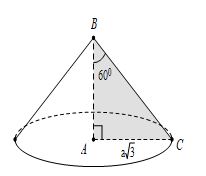
Lời giải

Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.

Theo giả thiết dễ suy ra đường tròn đáy có bán kính là:

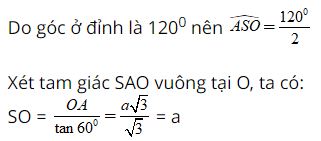
Do đó chiều cao hình nón là h = SO= a.

Vậy thể tích khối nón là

V = 1/3.π(2R)².h = 1/3.π.3a².a = πa³

Ví dụ 5: Bác Ba mua một cái xô hình nón cụt để đựng nước đổ vào bể nước 1m³. Biết xô có bán kính 2 đáy lần lượt là 20 cm và 25 cm. Chiều cao 30 cm. Bác Ba dự tính múc khoảng 20 xô thì đầy bể. Theo bạn bác tính có chuẩn không?

Lời giải:

Thể tích nước múc được bằng thể tích của xô nước

Thể tích của xô là:

V = 1/3 π(20² + 25² +20.25).30 = 15250π

=> Sau 20 lần múc, bác Ba múc được 9581853 cm³ ≈ 0,958m³ <1

Do vậy bác chưa thể múc đầy bể được.

Hy vọng với những thông tin mà chúng tôi vừa chia sẻ có thể giúp các bạn nhớ lại các công thức tính thể tích khối nón tròn xoay, cụt để áp dụng vào làm bài tập nhanh chóng nhé. Cảm ơn các bạn đã theo dõi bài viết của chúng tôi