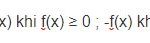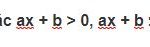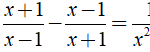Phương trình bậc nhất một ẩn là gì? Cách giải phương trình bậc nhất một ẩn có VD minh họa
Trong chương trình THPT nội dung về phương trình bậc nhất một ẩn và cách giải là một phần kiến thức cực kỳ quan trọng. Đây cũng không phải phần kiến thức khó “nhai” gì hết. Tuy nhiên, nếu không chăm chú nghe giảng thì vẫn sẽ bị thiếu hụt đi vài phần. Vậy nên chúng tôi đã củng cố lại cho các bạn học sinh kiến thức về phương trình bậc nhất 1 ẩn và cách giải ngay tại đây rồi đó.
Tham khảo thêm:
- Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp và bài tập có lời giải
- Phân tích đa thức thành nhân tử chung và bài tập có lời giải từ A- Z
- Chia đa thức với đơn thức là gì? Quy tắc chia đa thức với đơn thức và bài tập có lời giải chính xác 100%
Nội Dung
Phương trình bậc nhất một ẩn là gì?
Phương trình có dạng ax + b = 0, với a và b là hai số đã cho và a ≠ 0, được gọi là phương trình bậc nhất một ẩn.
Ví dụ:
Phương trình 2x – 3 = 0 là phương trình bậc nhất ẩn x.
Phương trình y – 4 = 2 là phương trình bậc nhất ẩn y.
Quy tắc biến đổi phương trình
Quy tắc chuyển vế: Trong một phương trình, ta có thể chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó.
Ví dụ: Giải phương trình x + 3 = 0
Giải: Ta có x + 3 = 0 ⇔ x = – 3. (chuyển hạng tử + 3 từ vế trái sang vế phải và đổi thành – 3 ta được x = – 3 )
Quy tắc nhân với một số: Trong một phương trình, ta có thể:
- Nhân cả hai vế với cùng một số khác 0.
- Chia cả hai vế cho cùng một số khác 0.
- Phương trình dạng ax + b = 0 với a 0 luôn có một nghiệm duy nhất x= -b/a
Ví dụ: Giải phương trình x/2 = – 2.
Giải: Ta có x/2 = – 2 ⇔ 2.x/2 = – 2.2 ⇔ x = – 4. (nhân cả hai vế với số 2 ta được x = – 4 )
Cách giải phương trình bậc nhất một ẩn
Để giải phương trình một ẩn ta có thể làm theo các bước như sau:
- Bước 1: Chuyển vế ax = – b.
- Bước 2: Chia hai vế cho a ta được: x = – b/a.
- Bước 3: Kết luận nghiệm: S = { – b/a }.
Ta có thể trình bày ngắn gọn như sau: ax + b = 0 ⇔ ax = – b ⇔ x = – b/a.
Vậy phương trình có tập nghiệm là S = { – b/a }.
Chú ý: Cho phương trình ax + b = 0 (1)
- Nếu a= 0; b= 0 thì phương trình (1) có vô số nghiệm
- Nếu a= 0; b ≠ 0 thì phương trình (1) vô nghiệm
- Nếu a ≠ 0 phương trình (1) có một nghiệm duy nhất x= -b/a
Các dạng bài tập thường gặp của phương trình bậc nhất một ẩn
Dạng 1: Nhận dạng phương trình bậc nhất một ẩn
Phương pháp: Ta sử dụng định nghĩa: Phương trình dạng ax + b = 0, với a và b là hai số đã cho và a ≠ 0 được gọi là phương trình bậc nhất một ẩn.
Ví dụ 1: Giải các phương trình sau:
a) 7x – 35 = 0
b) 4x – x – 18 = 0
c) x – 6 = 8 – x
Lời giải:
a) Ta có: 7x – 35 = 0 ⇔ 7x = 35 ⇔ x = 35/7 = 5.
Vậy phương trình có nghiệm là x = 5.
b) Ta có: 4x – x – 18 = 0 ⇔ 3x – 18 = 0 ⇔ 3x = 18 ⇔ x = 18/3 = 6.
Vậy phương trình có nghiệm là x = 6.
c) Ta có: x – 6 = 8 – x ⇔ 2x = 14 ⇔ x = 14/2 = 7.
Vậy phương trình có nghiệm là x = 7.
Ví dụ 2: Giải các phương trình sau:
a, 2x – 1 = 3
b, y/2 + 3 = 4
c, – 4x + 7 = – 1
Lời giải:
a, Ta có: 2x – 1 = 3 ⇔ 2x = 1 + 3 ⇔ 2x = 4
⇔ x = 4/2 ⇔ x = 2.
Vậy nghiệm của phương trình là x = 2.
b, Ta có: y/2 + 3 = 4 ⇔ y/2 = 4 – 3 ⇔ y/2 = 1
⇔ y = 2.1 ⇔ y = 2.
Vậy nghiệm của phương trình là y = 2.
c, Ta có: – 4x + 7 = – 1 ⇔ – 4x = – 1 – 7 ⇔ – 4x = – 8
⇔ x = – 8/ – 4 ⇔ x = 2.
Vậy phương trình có tập nghiệm là S = { 2 }.
Dạng 2: Giải và biện luận phương trình bậc nhất một ẩn.
Phương pháp: Ta dùng các quy tắc chuyển vế và quy tắc nhân với một số để giải phương trình.
Ví dụ: Giải các phương trình sau:
a, x – 4 = 0
b, 3/4 + x = 0
c, o,5 – x = 0
Lời giải:
a, Ta có: x = 0 + 4 (chuyển vế -4 từ VT sang VP)
⇔ x = 4
Vậy phương trình có nghiệm duy nhất là x = 4
b,Ta có 3/4 + x = 0 ( chuyển vế 3/4 từ VT sang VP )
⇔ x= 3/4
Vậy phương trình có nghiệm duy nhất là x= 3/4
c, Ta có 0,5 – x = 0 ( chuyển vế 0,5 từ VT sang VP )
⇔ x = 0,5
Vậy phương trình có nghiệm duy nhất là x = 0,5
Dạng 3: Giải các phương trình quy về phương trình bậc nhất một ẩn
Phương pháp: Cách giải phương trình đưa được về dạng
Nếu phương trình có mẫu số thì ta thực hiện các bước:
- Quy đồng mẫu hai vế
- Nhân hai vế với mẫu chung để khử mẫu
- Chuyển các hạng tử chứa ẩn sang một vế, các hằng số sang vế kia
- Thu gọn và giải phương trình nhận được.
Nếu phương trình không chứa mẫu thì ta sử dụng các quy tắc chuyển vế, quy tắc nhân, phá ngoặc và sử dụng hằng đẳng thức để biến đổi.
Nếu phương trình có chứa dấu giá trị tuyệt đối thì ta phá dấu giá trị tuyệt đối hoặc sử dụng
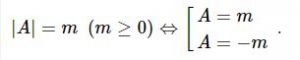
Ví dụ 1: Giải phương trình:
![]()
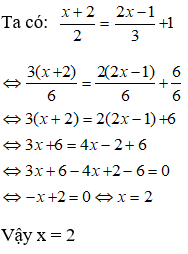
Ví dụ 2: Giải phương trình: 4x – 2(x + 1) = 3x + 2
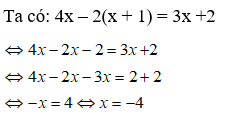
Ví dụ 3: Số nghiệm của phương trình (x – 1)2 = x2 + 4x – 3 là:
ta có: (x – 1)2 = x2 + 4x – 3
⇔ x2 – 2x + 1 = x2 + 4x – 3
⇔ x2 – 2x + 1 – x2 – 4x + 3 = 0
⇔ -6x + 4 = 0
⇔ x = 2/3
Vậy phương trình có nghiệm duy nhất x = 2/3
Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình