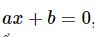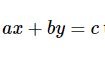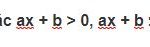Lý thuyết và cách giải bất phương trình bậc nhất hai ẩn có VD minh họa chi tiết từ A – Z

Nội dung bài học sẽ giới thiếu đến các bạn khái niệm cơ bản bất phương trình bậc nhất hai ẩn và cách biểu diễn tập nghiệm của bất phương trình bậc nhất hai ẩn

Tham khảo thêm:

• Phân tích đa thức thành nhân tử chung và bài tập có lời giải từ A- Z
• Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp và bài tập có lời giải
• Rút gọn phân số là gì? Khái niệm rút gọn phân số và bài tập có lời giải chính xác 100%

Bất phương trình bậc nhất hai ẩn là gì?

Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là ax + by ≤ c (1)

(ax + by < c; ax + by ≥ c; ax + by > c)

Trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số. Cặp số (x₀; y₀) sao cho ax₀ + by₀ ≤ c là một bất đẳng thức đúng được gọi là một nghiệm của bất phương trình ax + by ≤ c.

Tập nghiệm của bất phương trình bạc nhất hai ẩn

Trong mặt phẳng tọa độ Oxy, tập hợp các điểm có tọa độ là nghiệm của bất phương trình (1) được gọi là miền nghiệm của nó.

Từ đó ta có quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) của bất phương trình ax + by ≤ c như sau (tương tự cho bất phương trình ax + by ≥ c)

• Bước 1. Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng Δ: ax + by = c.
• Bước 2. Lấy một điểm Mo(xo; yo) không thuộc Δ (ta thường lấy gốc tọa độ )
• Bước 3. Tính ax_o + by_o và so sánh ax_o + by_o với c.
• Bước 4. Kết luận

Nếu ax_o + by_o < c thì nửa mặt phẳng bờ Δ chứa M0 là miền nghiệm của ax_o + by_o ≤ c

Nếu ax_o + by_o > c thì nửa mặt phẳng bờ Δ không chứa M0 là miền nghiệm của ax_o + by_o ≤ c

Chú ý: Miền nghiệm của bất phương trình ax_o + by_o ≤ c bỏ đi đường thẳng ax + by = c là miền nghiệm của bất phương trình ax_o + by_o < c

Các dạng toán thường gặp ở bất phương trinh bậc nhất hai ẩn

Bài tập 1: Một công ty kinh doanh thương mại chuẩn bị cho một đợt khuyến mại nhằm thu hút khách hàng bằng cách tiến hành quảng cáo sản phẩm của công ty trên hệ thống phát thanh và truyền hình. Chi phí cho 1 phút quảng cáo trên sóng phát thanh là 800.000 đồng, trên sóng truyền hình là 4.000.000 đồng. Đài phát thanh chỉ nhận phát các chương trình quảng cáo dài ít nhất là 5 phút.

Do nhu cầu quảng cáo trên truyền hình lớn nên đài truyền hình chỉ nhận phát các chương trình dài tối đa là 4 phút. Theo các phân tích, cùng thời lượng một phút quảng cáo, trên truyền hình sẽ có hiệu quả gấp 6 lần trên sóng phát thanh. Công ty dự định chi tối đa 16.000.000 đồng cho quảng cáo. Công ty cần đặt thời lượng quảng cáo trên sóng phát thanh và truyền hình như thế nào để hiệu quả nhất?

Lời giải:

Gọi thời lượng công ty đặt quảng cáo trên sóng phát thanh là x (phút), trên truyền hình là y (phút). Chi phí cho việc này là: 800.000x + 4.000.000y (đồng)

Mức chi này không được phép vượt qúa mức chi tối đa, tức:

800.000x + 4.000.000y ≤ 16.000.000

hay: x + 5y – 20 ≤ 0

Do các điều kiện đài phát thanh, truyền hình đưa ra, ta có: x ≥ 5; y ≤ 4

Đồng thời do x,y là thời lượng nên x ≥ 0; y ≤ 0. Hiệu quả chung của quảng cáo là: x + 6y

Bài toán trở thành: Xác định x, y sao cho: M(x,y)= x + 6y đạt giá trị lớn nhất.

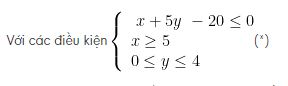
Trước tiên ta xác định miền nghiệm của hệ bất phương trình (*)

Trong mặt phẳng tọa độ vẽ các đường thẳng (d) : x + 5y – 20 =, (d”):x =5, (d”): y=4

Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tam giác) không tô màu trên hình vẽ

Giá trị lớn nhất của M(x,y)= x + 6y đạt tại một trong các điểm (5;3), (5;0), (20;0)

Ta có M(5;3)=23, M(5;0)=5, (20;0)=20 suy ra giá trị lớn nhất của M(x,y) bằng 23 tại (5;3) tức là nếu đặt thời lượng quảng cáo trên sóng phát thanh là 5 phút và trên truyền hình là 3 phút thì sẽ đạt hiệu quả nhất.

Bài tập 2: Cho bất phương trình bậc nhất hai ẩn x + 2y ≥ 0.

a) Hãy chỉ ra ít nhất hai nghiệm của bất phương trình trên.

b) Với y = 0, có bao nhiêu giá trị của x thỏa mãn bất phương trình đã cho?

Lời giải:

a) Với x = 1, y = 2, thay vào bất phương trình ta có: 1 + 2.2 = 5 ≥ 0 (luôn đúng)

Suy ra (1;2) là nghiệm của bất phương trình đã cho.

Với x = -2, y = 1, thay vào bất phương trình ta có: -2 + 2.1 = 0 ≥ 0 (luôn đúng)

Suy ra (-2;1) là nghiệm của bất phương trình đã cho.

Với x = 7, y = -2, thay vào bất phương trình ta có: 7 + 2.(-2) = 3 ≥ 0 (luôn đúng)

Suy ra (7;-2) là nghiệm của bất phương trình đã cho.

b) Thay y = 0 vào bất phương trình đã cho ta được: x + 2.0 ≥ 0 ⇔ x ≥ 0.

Vậy với y = 0 thì có vô số giá trị của x mà x ≥ 0 thỏa mãn bất phương trình đã cho.

Bài tập 3: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

a) 2x + 3y > 6;

b) 2²x + y ≤ 0;

c) 2x² – y ≥ 1.

Lời giải:

Bất phương trình bậc nhất hai ẩn x,y có dạng tổng quát là: ax + by > c ( ax + by < c, ax + by ≥ 0, ax + by ≤ 0)

Trong đó a, b, c là số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số.

Do đó:

a) 2x + 3y > 6 là bất phương trình bậc nhất hai ẩn với a = 2, b = 3 và c = 6;

b) 2²x + y ≤ 0 là bất phương trình bậc nhất hai ẩn với a = 2² = 4, b = 1 và c = 0.

c) 2x² – y ≥ 1 không là bất phương trình bậc nhất hai ẩn do ẩn x có bậc là 2.

Bài tập 4: Cặp số (x; y) = (100; 100) thỏa mãn bất phương trình bậc nhất hai ẩn nào trong hai bất phương trình thu được ở HĐ1? Từ đó cho biết rạp chiếu phim có phải bù lỗ hay không nếu bán được 100 vé loại 1 và 100 vé loại 2. Trả lời câu hỏi tương tự với cặp số (x; y) = (150; 150).

Lời giải:

+) Xét cặp số (x; y) = (100; 100).

– Thay x = 100 và y = 100 vào bất phương trình 50x + 100y ≥ 20 000 ta được: 50.100 + 100.100 ≥ 20 000 ⇔ 15 000  ≥  20 000 (vô lí).

Do đó cặp số (100; 100) không thỏa mãn bất phương trình 50x + 100y ≥ 20 000.

– Thay x = 100 và y = 100 vào bất phương trình 50x + 100y < 20 000 ta được: 50.100 + 100.100 < 20 000 ⇔ 15 000  <  20 000 (luôn đúng).

Do đó cặp số (100; 100) thỏa mãn bất phương trình 50x + 100y < 20 000.

Vì vậy nếu rạp chiếu phim bán được 100 vé loại 1 và 100 vé loại 2 thì số tiền thu được là 15 triệu đồng và rạp chiếu phim phải bù lỗ.

+) Xét cặp số (x; y) = (150; 150).

– Thay x = 150 và y = 150 vào bất phương trình 50x + 100y ≥ 20 000 ta được: 50.150 + 100.150 ≥ 20 000 ⇔ 22 500  ≥  20 000 (luôn đúng).

Do đó cặp số (150; 150) thỏa mãn bất phương trình 50x + 100y ≥ 20 000.