Phương trình chứa dấu giá trị tuyệt đối là gì? Cách giải phương trình chứa dấu giá trị tuyệt đối kèm bài tập có lời giải

Phương trình chứa dấu giá trị tuyệt đối được thptchuyenlamson.vn sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán hiệu quả hơn. Mời các bạn tham khảo.

Tham khảo thêm:

• Số thực là gì? Tính chất của số thực và bài tập chi tiết từ A – Z
• Hỗn số là gì? Cách chuyển đổi của hỗn số và bài tập chính xác 100%
• Số hữu tỉ là gì? Cách so sánh số hữu tỉ và bài tập có lời giải từ A – Z

Cách giải phương trình chứa dấu giá trị tuyệt đối

Giá trị tuyệt đối của f(x), được kí hiệu là | f(x) |, ta định nghĩa như sau:

| f(x) | = f(x) khi f(x) ≥ 0 ; -f(x) khi f(x) < 0

Giải một số phương trình chứa dấu giá trị tuyệt đối

Phương pháp chung:

• Bước 1: Áp dụng định nghĩa giá trị tuyệt đối để loại bỏ dấu giá trị tuyệt đối
• Bước 2: Rút gọn hai vế của phương trình, giải phương trình
• Bước 3: Chọn nghiệm thích hợp trong từng trường hợp đang xét
• Bước 4: Kết luận nghiệm

Một số dạng cơ bản:

Dạng | A | = | B | ⇔ A = B hay A = – B.

Dạng phương trình có chứa nhiều dấu giá trị tuyệt đối

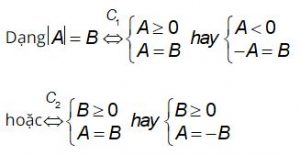
+ Xét dấu các biểu thức chứa ẩn nằm trong dấu GTTĐ.

+ Chia trục số thành nhiều khoảng sao cho trong mỗi khoảng, các biểu thức nói trên có dấu xác định.

+ Xét từng khoảng, khử các dấu GTTĐ, rồi giải PT tương ứng trong trường hợp đó.

+ Kết hợp các trường hợp đã xét, suy ra số nghiệm của PT đã cho.

Các dạng bài tập thường gặp của phương trình chứa giá trị tuyệt đối

Bài tập 1: Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức sau:

a) A = | x – 1 | + 3 – x khi x ≥ 1.

b) B = 3x – 1 + | – 2x | khi x < 0.

Lời giải:

a) Khi x ≥ 1 ta có x – 1 ≥ 0 nên | x – 1 | = x – 1

Do đó A = | x – 1 | + 3 – x = x – 1 + 3 – x = 2.

b) Khi x < 0 ta có – 2x > 0 nên | – 2x | = – 2x

Do đó B = 3x – 1 + | – 2x | = 3x – 1 – 2x = x – 1.

Bài tập 2: Giải phương trình | 4x | = 3x + 1

Lời giải:

Ta có | 4x | = 3x + 1

+ Với x ≥ 0 ta có | 4x | = 4x

Khi đó phương trình trở thành 4x = 3x + 1

⇔ 4x – 3x = 1 ⇔ x = 1.

Giá trị x = 1 thỏa mãn điều kiện x ≥ 0, nên 1 là một nghiệm của phương trình đã cho

+ Với x < 0 ta có | 4x | = – 4x

Khi đó phương trình trở thành – 4x = 3x + 1

⇔ – 4x – 3x = 1 ⇔ – 7x = 1 ⇔ x = – 1/7.

Giá trị x = – 1/7 thỏa mãn điều kiện x < 0, nên – 1/7 là một nghiệm cần tìm.

Vậy phương trình đã cho có tập nghiệm là S = { – 1/7;1 }

Bài tập 3: Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức sau:

a) A = 3x + 2 + | 5x | với x > 0.

b) A = | 4x | – 2x + 12 với x < 0.

c) A = | x – 4 | – x + 1 với x < 4

Lời giải:

a) Với x > 0 ⇒ | 5x | = 5x

Khi đó ta có: A = 3x + 2 + | 5x | = 3x + 2 + 5x = 8x + 2

Vậy A = 8x + 2.

b) Ta có: x < 0 ⇒ | 4x | = – 4x

Khi đó ta có: A = | 4x | – 2x + 12 = – 4x – 2x + 12 = 12 – 6x

Vậy A = 12 – 6x.

c) Ta có: x < 4 ⇒ | x – 4 | = 4 – x

Khi đó ta có: A = | x – 4 | – x + 1 = 4 – x – x + 1 = 5 – 2x.

Vậy A = 5 – 2x

Bài tập 4: Giải các phương trình sau:

a) | 2x | = x – 6

b) | – 5x | – 16 = 3x

c) | 4x | = 2x + 12

d) | x + 3 | = 3x – 1

Lời giải:

a) Ta có: | 2x | = x – 6

+ Với x ≥ 0, phương trình tương đương: 2x = x – 6 ⇔ x = – 6.

Không thỏa mãn điều kiện x ≥ 0.

+ Với x < 0, phương trình tương đương: – 2x = x – 6 ⇔ – 3x = – 6 ⇔ x = 2.

Không thỏa mãn điều kiện x < 0.

Vậy phương trình đã cho vô nghiệm.

b) Ta có: | – 5x | – 16 = 3x

+ Với x ≥ 0, phương trình tương đương: 5x – 16 = 3x ⇔ 2x = 16 ⇔ x = 8

Thỏa mãn điều kiện x ≥ 0

+ Với x < 0, phương trình tương đương: – 5x – 16 = 3x ⇔ 8x = – 16 ⇔ x = – 2

Thỏa mãn điều kiện x < 0

Vậy phương trình đã cho có tập nghiệm là S = { – 2;8 }

c) Ta có: | 4x | = 2x + 12

+ Với x ≥ 0, phương trình tương đương: 4x = 2x + 12 ⇔ 2x = 12 ⇔ x = 6

Thỏa mãn điều kiện x ≥ 0

+ Với x < 0, phương trình tương đương: – 4x = 2x + 12 ⇔ – 6x = 12 ⇔ x = – 2

Thỏa mãn điều kiện x < 0

Vậy phương trình đã cho có tập nghiệm là S = { – 2;6 }

d) Ta có: | x + 3 | = 3x – 1

+ Với x ≥ – 3, phương trình tương đương: x + 3 = 3x + 1 ⇔ – 2x = – 2 ⇔ x = 1.

Thỏa mãn điều kiện x ≥ – 3

+ Với x < – 3, phương trình tương đương: – x – 3 = 3x + 1 ⇔ – 4x = 4 ⇔ x = – 1

Không thỏa mãn điều kiện x < – 3

Vậy phương trình đã cho có tập nghiệm là S = { 1 }

Bài 5: Giải phương trình:

a, A = | 4x | + 2x – 1 với x < 0

Ta có: x < 0 ⇒ | 4x | = – 4x

Khi đó ta có: A = | 4x | + 2x – 1 = – 4x + 2x – 1 = – 2x – 1

b, B= | 3x + 1 | = 5

Ta có: | 3x + 1 | = 5 ⇒ 3x+1=5 ⇒ x= 4/3; 3x +1= -5 ⇒ x= -2

Vậy tập nghiệm của phương trình đã cho là S = { – 2;4/3 }

Bài 6: Giá trị m để phương trình | 3 + x | = m có nghiệm x = – 1 là?

Giải:

Phương trình đã cho có nghiệm x = – 1 nên ta có: | 3 + ( – 1 ) | = m ⇔ m = 2.

Vậy m = 2 là giá trị cần tìm.

b, Giá trị của m để phương trình | x – m | = 2 có nghiệm là x = 1 ?

Phương trình có nghiệm x = 1, khi đó ta có:

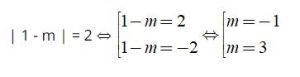
Vậy giá trị m cần tìm là m ∈ { – 1;3 }

Bài 7: Nghiệm nhỏ nhất của phương trình |2 + 3x| = |4x – 3| là

Giải:

Ta có |2 + 3x| = |4x – 3|

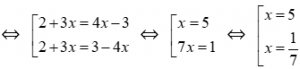
Vậy nghiệm nhỏ nhất của phương trình là x = 1/7

Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình