Hệ Thức Lượng Trong Tam Giác Vuông, Cân, Thường Lớp 8, 9, lớp 10 Có VD
Bạn có bài toán về hệ thức lượng trong tam giác nhưng bạn lại không biết cách làm như thế nào bởi bạn không lắm được kiến thức. Chính vì vậy, bài viết này THPT Chuyên Lam Sơn muốn chia sẻ đến các bạn hệ thức lượng trong tam giác vuông, cân, thường các bạn cần học thuộc để áp dụng vào giải bài tập.
Nội Dung
Hệ thức lượng giác trong tam giác vuông
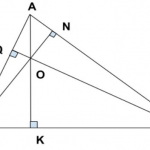
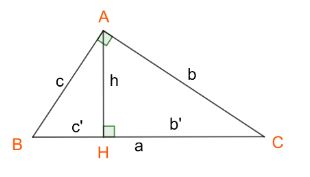
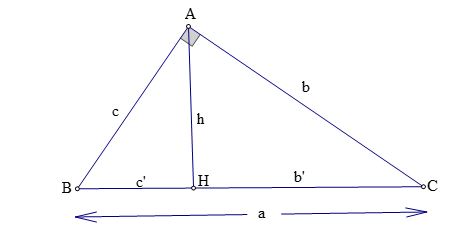
Cho tam giác ABC vuông góc tại đỉnh A (Aˆ = 90º), ta có:
- b² = a.b’; c² = a.c’
- Định lý Pitago: a² = b² + c²
- a.h = b.c
- h² = b’.c’
- ¹⁄h² = ¹⁄b² + ¹⁄c²
1. Tỉ số lượng giác của góc nhọn
a. Định nghĩa
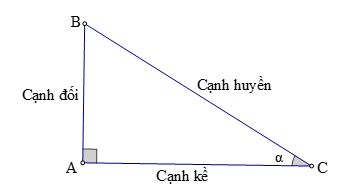
- Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sinα.
- Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu là cosα.
- Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu là tanα.
- Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α, kí hiệu là cotα
Hay sinα = AB/BC; cosα = AC/BC; tanα = AB/AC; cotα = AC/AB.
Nhận xét: Nếu α là một góc nhọn thì 0 < sinα < 1; 0 < cosα < 1; tanα > 0; cotα > 0
b. Định lý:
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Tức là: Cho hai góc α, β có α + β = 90°
Khi đó: sinα = cosβ; cosα = sinβ; tanα = cotβ; cotα = tanβ.
c. Một số hệ thức cơ bản
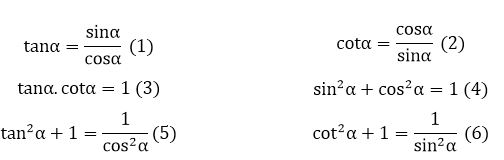
d. So sánh các tỉ số lượng giác
1. Cho α, β là hai góc nhọn. Nếu α < β thì:
- sinα < sinβ; tanα < tanβ
- cosα > cosβ; cotα > cotβ
2. sinα < tanα và cosα < cotα
3. Cho góc nhọn x (0o < 0 < 90°), ta có:
- sinx = cos (90° – x)
- Cosx = sin (90° – x)
- tanx = cot (90° – x)
- cotx = tan (90° – x)
2. Hệ thức về góc và cạnh trong tam giác vuông
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
- Cạnh huyền nhân với sin góc đối hay nhân với côsin góc kề.
- Cạnh góc vuông kia nhân với tan của góc đối hay nhân với cotg của góc kề.
b = a.sinB = a.cosC; c = a.sinC = a.cosB; b = c.tanB = c.cotC; c = b.tanC = b.cotC
Chú ý: Trong một tam giác vuông nếu cho trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và không kể góc vuông) thì ta sẽ tìm được các yếu tố còn lại.
Các hệ thức lượng trong tam giác thường
1. Định lý cosin
Định lí: Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với Cosin của góc xen giữa chúng.
Ta có các hệ thức sau:
a² = b² + c² – 2bc.cosA; (1)
b² = c² + a² – 2ca.cosB; (2)
c² = a² + b² – 2ab.cosC. (3)
Hệ quả của định lí cosin:
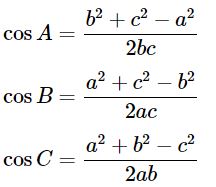
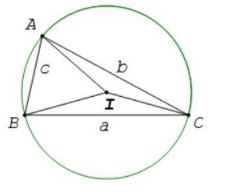
2. Định lí sin
Định lí: Trong tam giác ABC bất kỳ, tỉ số giữa một cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là a⁄sinA = b⁄sinB = c⁄sinC = 2R với R là bán kính đường tròn ngoại tiếp tam giác
Xem ngay: Định Lý và Công thức Sin Cos Tan lớp 9, lớp 10, lớp 11, lớp 12
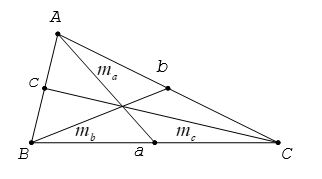
3. Độ dài đường trung tuyến
Cho tam giác ABC có các cạnh BC = a,CA = b và AB = c. Gọi ma, mb và mc là độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A, B, C của tam giác. Ta có
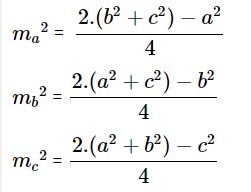
4. Công thức tính diện tích tam giác
Diện tích của tam giác ABC được tính theo một trong các công thức sau:
S = ½a.b.sinC = ½b.c.sinA = ½c.asinB (1)
S = abc/4R (2)
S = pr (3)
S = √p(p-a)(p-b)(p-c) (công thức Hê rông) (4)
Trong đó:
- S là diện tích tam giác
- R là bán kính đường tròn ngoại tiếp tam giác;
- r là bán kính đường tròn nội tiếp tam giác;
- a, b, c là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB;
Tham khảo thêm: Công thức tính diện tích tam giác vuông, cân, đều kèm VD
Các dạng bài tập hệ thức trong tam giác có lời giải
Dạng 1: Tính toán các đại lượng.
Phương pháp giải: Vận dụng các định lí sin, cosin, trung tuyến, diện tích và quan hệ giữa các đại lượng cần tính, các dạng tam giác đặc biệt.
Ví dụ 1: Cho tam giác ABC có AB = 1cm , AC = 2cm và Aˆ = 120° . Tính BC
Lời giải
Áp dụng định lí cosin ta có:
BC² = AB² + AC² – 2AB.AC.cos Aˆ
BC² = 1² + 2² – 2.1.2.cos120°
BC² = 1 + 4 – 4.(-½) = 7
BC = √7 cm
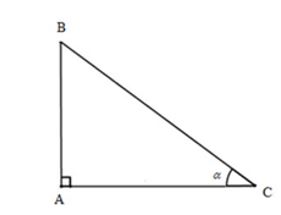
Ví dụ 2: Cho tam giác ABC vuông tại A. Biết cos B = 0,8. Hãy tính các tỉ số lượng giác của góc C.
Lời giải
Xét tam giác ABC vuông tại A có Aˆ = 90°
Bˆ + Cˆ = 90°
Do đó Bˆ và Cˆ là hai góc phụ nhau
⇒ sinC = cosB = 0,8
Từ kết quả bài 14 ta có:
sin2C + cos2C = 1
⇔ cos2C = 1 – sin2C
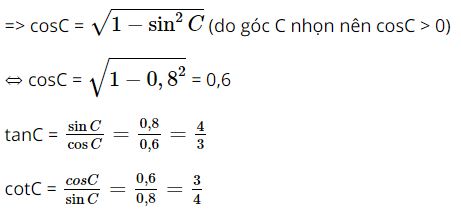
Vậy sinC = 0,8; cosC = 0,6; tanC = 4⁄3;cotC = ¾
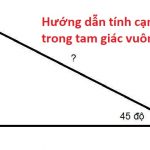
Ví dụ 3: Cho tam giác vuông có một góc 60° và cạnh huyền có độ dài là 8. Hãy tìm độ dài của cạnh đối diện với góc 60°.
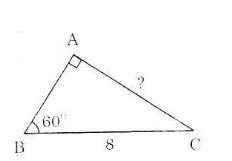
Giả sử ta có tam giác ABC như trên hình. Ta có:
sinB = AC/BC
⇒AC = BC.sinB = 8.sin60° = 4√3
Dạng 2: Chứng minh hệ thức, tính giá trị các biểu thức
Phương pháp giải: Vận dụng các phương pháp chứng minh đẳng thức: biến đổi sao cho hai vế bằng nhau, từ giả thiết ban đầu dẫn đến một đẳng thức đã được công nhận là đúng,… Sử dụng các định lí trong tam giác vuông, tam giác thường, các hệ thức lượng trong tam giác.
Ví dụ 1: Cho hình bình hành ABCD, chứng minh rằng BD² + AC² = 2(AB² + AD²)
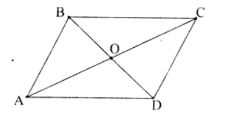
Lời giải
Ta có O là tâm hình bình hành ABCD ⇒ O là trung điểm của AC.
BO là trung tuyến của tam giác ABC ứng với cạnh AC.
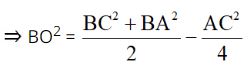
4BO² = 2(BC² + BA²) – AC² (1)
Mà O là trung điểm của BD ⇒ BD = 2BO ⇒ BD² = 4BO² (1)
⇒ BD² = 2(CB² + AB²) – AC²
⇒ BD² + AC² = 2(CB² + AB²)
⇒ BD² + AC² = 2(AB² + AD²) ( do AD = CB ) (điều cần phải chứng minh)
Ví dụ 2: Chứng minh rằng giá trị của các biểu thức sau không phụ thuộc vào số đo của góc nhọn α:
a) A = cos4α + 2cos²αsin²α + sin4α
b) B = sin4α + cos²α.sin²α + cos²α
Lời giải
a) A = cos4α + 2cos²αsin²α + sin4α
= (cos²α)² + 2cos²αsin²α + (sin²α)²
= (cos²α + sin²α)² (do sin²α + cos²α = 1)
= 1
b) B = sin4α + cos²α.sin²α + cos²α
= (sin4α + cos²α . sin²α) + cos²α
= sin²α . (sin²α + cos²α) + cos²α (do sin²α + cos²α = 1)
sin²α . 1 + cos²α = 1
Ví dụ 3: Chứng minh định lý sin: Trong tam giác nhọn, độ dài các cạnh tỉ lệ với sin của các góc đối diện a/sinA = b/sinB = c/sinC
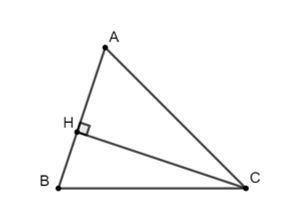
Lời giải
Vẽ đường cao CH
Xét ΔAHC vuông tại H có: sinA = CH/AC
Xét ΔAHB vuông tại H có: sinB = CH/BC
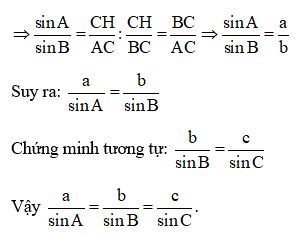
Dạng 3: Chứng minh tam giác.
Phương pháp giải: Áp dụng các hệ thức lượng trong tam giác, các định lí, công thức về diện tích, đường trung tuyến và các bất đẳng thức, hằng đẳng thức cơ bản.
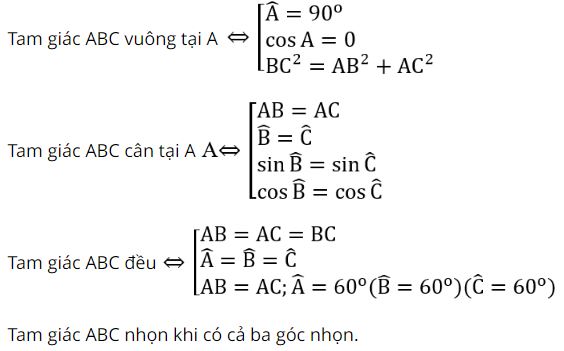
Ví dụ 1: Cho tam giác ABC. Chứng minh Aˆ nhọn khi và chỉ khi BC² < AB² + AC²
Áp dụng định lí cosinAˆ ta có:
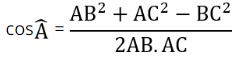
Mà AB.AC luôn lớn hơn 0 nên cosAˆ cùng dấu với biểu thức (AB² + AC²- BC²)
Aˆ nhọn ⇒ 0° < Aˆ > 90° ⇒ cosAˆ > 0
⇒ AB² + AC²- BC² > 0
⇒ BC² < AB² + AC²
Ví dụ 2: Cho tam giác ABC có nửa chu vi p và diện tích S. Xét dạng tam giác ABC khi biết S = p.(p – BC)
Lời giải
Áp dụng công thức tính diện tích ta có:
S = √p(p-BC)(p-AB)(p-AC)
⇒ √p(p-BC)(p-AB)(p-AC) = p(p-BC)
⇒ √p(p-BC)(p-AB)(p-AC) = √p(p-BC)
⇒ (p-AB)(p-AC) – p.(p-BC)
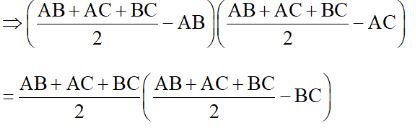
⇒ (AC + BC – AB)(AB + BC – AC) = (AB + AC + BC)(AB+AC-BC)
⇒ BC² – (AC – AB)² = (AB+AC)² – BC²
⇒ BC² – (AC² – 2AC.AB + AB²) = AB² + 2AB.AC + AC² – BC²
⇒ 2BC² = 2AB² + 2AC²
⇒ BC² = AC² + AB²
Vậy tam giác ABC là tam giác vuông tại A.
Dạng 4: Giải tam giác và các bài toán thực tế.
Phương pháp giải: Giải tam giác là tìm số đo các cạnh, các góc còn lại trong tam giác khi biết các giải thiết, áp dụng các hệ thức lượng, định lí, công thức tính diện tích, đường trung tuyến,… Bài toán thực tế được giải bằng cách chuyển về bài toán tam giác để xác định số đo được yêu cầu.
Ví dụ 1. Cho ΔABC có AB = 12, BC = 15, AC = 13
a. Tính số đo các góc của ΔABC
b. Tính độ dài các đường trung tuyến của ΔABC
c. Tính diện tích tam giác ABC, bán kính đường tròn nội tiếp, bán kính đường tròn ngoại tiếp tam giác ABC
d. Tính độ dài đường cao nối từ các đỉnh của tam giác ABC
Lời giải
a. Áp dụng hệ thức lượng trong tam giác ta có:
AB² = AC² + BC² – 2AC.BC.cosACBˆ
⇔ 12² = 13² + 15² – 2.13.15.cosACBˆ
⇔ cosACBˆ = 25⁄39 ⇒ ACBˆ ≈50°7′

c. Để tính được diện tích một cách chính xác nhất ta sẽ áp dụng công thức Hê – rông
Nửa chu vi tam giác ABC
p = (AB + AC + BC) : 2 = (12+13+15):2 = 20
Diện tích tam giác ABC:
S = √p(p-AB)(p-AC)(p-BC) = 20√14
Bán kính đường tròn ngoại tiếp R của tam giác ABC:

Sau khi đọc xong bài viết của chúng tôi có thể giúp các bạn củng cố lại các kiến thức về hệ thức lượng trong tam giác vuông, cân, thường để vận dụng vào làm bài tập nhé