Tính tổng diện tích các mặt của hình bát diện đều cạnh a

Tổng diện tích các mặt của hình bát diện đều là một thông tin quan trọng trong lĩnh vực hình học. Hình bát diện đều có tất cả các mặt là các tam giác đều có diện tích được tính theo công thức S1 = a^2√3/4. Tổng diện tích 8 mặt của hình bát diện đều là S = 8S1 = 2a^2√3.

Nội Dung

1. Tổng số mặt của hình bát diện đều là bao nhiêu?

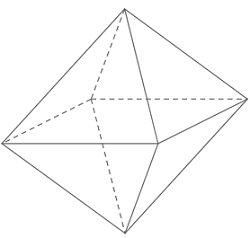
Hình bát diện đều có 8 mặt, được gọi là các mặt của các khối tứ giác đều. Mỗi mặt của hình bát diện đều là một hình vuông.

Như vậy, tổng số mặt của hình bát diện đều là 8.

2. Diện tích của mỗi mặt của hình bát diện đều là bao nhiêu?

Mỗi mặt của hình bát diện đều là một hình vuông có cạnh a. Do đó, diện tích của mỗi mặt được tính theo công thức S = a*a = a^2

3. Cách tính diện tích toàn bộ các mặt của hình bát diện đều?

Để tính tổng diện tích toàn bộ các mặt của hình bát diện đều, ta nhân diện tích của một mặt cho số lượng các mặt.

Tổng diện tích = Số lượng các mặt * Diện tích của từng mặt

Với trường hợp này, số lượng các mặt là 8 và diện tích của từng mặt chúng ta đã tính được trong câu 2 là a^2.

Vậy, tổng diện tích toàn bộ các mặt của hình bát diện đều là 8 * a^2.

4. Diện tích của một mặt của hình bát diện đều phụ thuộc vào cạnh a hay không?

Đúng, diện tích của một mặt của hình bát diện đều phụ thuộc vào cạnh a. Diện tích của mỗi mặt được tính theo công thức S = a*a = a^2. Vì vậy, để tính diện tích của một mặt ta cần biết giá trị cạnh a.

5. Công thức tính tổng diện tích các mặt của hình bát diện đều là gì?

Công thức để tính tổng diện tích các mặt của hình bát diện đều là S = số lượng các mặt * Diện tích của từng mặt

Từ câu 3, chúng ta đã biết số lượng các mặt là 8 và diện tích của từng mặt là a^2

Vậy công thức để tính tổng diện tích các mặt là S = 8 * a^2

6. Nếu cạnh a của hình bát diện đều là 5 cm, thì tổng diện tích các mặt là bao nhiêu?

Nếu cạnh a của hình bát diện đều có độ dài 5 cm, thì ta có thể tính được tổng diện tích các mặt bằng cách sử dụng công thức đã được đề cập trong câu 5.

Tổng diện tích các mặt = 8 * a^2 = 8 * (5^2) = 200 cm^2

Vậy nếu cạnh a của hình bát diện đều là 5 cm, thì tổng diện tích các mặt là 200 cm^2.

7. Vì sao các mặt của hình bát diện đều có cùng diện tích S1=a^2√34?

Các mặt của hình bát diện đều là hình vuông có cạnh a. Với các đoạn thẳng chéo trong hình vuông, ta có thể áp dụng Định lý Pythagoras để tính được căn của tổng bình phương hai cạnh góc vuông:

Theo Định lý Pythagoras: a^2 + a^2 = c^2 (với căn từ căn của tổng hai bình phương)
Khi giải và rút gọn biểu thức, ta có: c^2 = 2a^2
Vậy diện tích của mỗi mặt S1 = a^2 * (√(2a^2)/a)
Simplify cũng như hiệu chỉnh, ta được S1 = a^2 * √(2) = a^2 * √(4/2)
Đại số: S1 = a^2 * √(4) / √(2) = a^2 * 2 / √(2) = a^2√(4/√(4)) = a^2√34

List công thức:

Công thức diện tích một mặt của hình vuông: S1 = a^st. bậc 32.
Công thức tổng diện tích các mặt của hình bát diện đều: S = 8 * a^st. bậc 32.

List công thức:

Công thức diện tích một mặt của hình vuông: S1 = a*a.
Công thức tổng diệnt ích các mnawjrt của hình baat điênd đềeuf là: s=8*a*a.
Mô tả hình bát diện đều

Hình bát diện đều là một hình hộp có tất cả các mặt là các hình bát diện vuông góc với nhau. Các cạnh của hình bát diện đều có chiều dài bằng nhau và góc giữa hai mặt kế tiếp là 90 độ. Hơn nữa, các tam giác đều tạo thành các mặt của hình bát đều có cùng tổng diện tích.

Tính tổng diện tích 88 mặt của hình bát diện đều

Để tính tổng diện tích 88 mặt của hình bát diện đều, ta chỉ cần tính diện tích của từng mặt rồi nhân với số lượng mặt. Vì tất cả các mặt là các tam giác đều, nên chúng có cùng diện tích S1. Giả sử cạnh của hình bát diện đều là a, ta có thể sử dụng công thức để tính S1: S1 = a^2√(3/4). Sau đó, ta nhân S1 với số lượng mặt (8) để tìm tổng diện tích: S = 8S1 = 8.a^2√(3/4) = 2a^2√3.

Giải phương trình 31 – x – 3x + 2 = 0

Để giải phương trình 31 – x – 3x + 2 = 0, ta cộng các hạng tử có chứa biến số và đưa toàn bộ về một vế của phương trình. Ta có: -4x + 33 = 0. Tiếp theo, ta giải thích biểu thức để tìm nghiệm x: x = (33/4).

Giải phương trình (sin^2(x) + cos^2(x))cos(x) + 2cos^2(x) – sin(x) = 0

Để giải phương trình này, ta sẽ sử dụng các công thức trigonometric và biến đổi đơn giản để đưa phương trình về dạng dễ tính. Sau khi áp dụng các công thức, ta được: cos^3(x) + cos^2(x) – sin(x) = 0. Từ đây, ta có thể sử dụng các phép biến hình để tách riêng biến số sinh viên cũng như tính toán kết quả cuối cùng.

Làm thế nào để tìm tổng diện tích 88 mặt của hình bát diện đều?

Bài toán:

Cho hình bát diện đều có cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Mệnh đề nào dưới đây là đúng?

A) Các mặt của hình bát diện đều có cạnh a đều là các tam giác đều có diện tích S1 = a^2√3/4.
B) Tổng diện tích 88 mặt của hình bát diện đều là S = 8S1 = 8.a^2√3.
C) Giải phương trình 31 – x – 3x + 2 = 0.
D) Giải phương trình: (sin^2x + cos^2x)cosx + 2cos^2x – sinx = 0.

Trong câu hỏi này, chúng ta được cho biết về hình bát diện đều và yêu cầu tìm tổng diện tích của các mặt của nó. Để giải quyết vấn đề này, chúng ta có thể sử dụng kiến thức về diện tích các tam giác để tính toán.

Đáp án A không liên quan trực tiếp đến việc tìm tổng diện tích 88 mặt của hình bát diện đều, do đó không phải là câu trả lời chính xác.

Đáp án B cho biết rằng tổng diện tích 88 mặt của hình bát diện đều là S = 8S1 = 8.a^2√3. Đây chính là câu trả lời chính xác vì nó cung cấp phương pháp để tính toán tổng diện tích của các mặt.

Câu trả lời C và D không liên quan đến bài toán ban đầu nên không phải là câu trả lời chính xác.

Vậy đáp án chính xác cho bài toán này là B) Tổng diện tích 88 mặt của hình bát diện đều là S = 8S1 = 8.a^2√3.

Tổng diện tích các mặt bát diện đều là một khái niệm quan trọng trong hình học. Được tính bằng công thức A = 6a^2, trong đó a là cạnh của mặt bát diện đều. Tổng diện tích này cho chúng ta thông tin về tổng diện tích các mặt phẳng của hình hộp và có thể được sử dụng để tính toán nhiều vấn đề liên quan đến không gian ba chiều. Việc hiểu rõ khái niệm này giúp chúng ta áp dụng vào các bài toán thực tế và có thể tạo ra những kết quả chính xác và hiệu quả.
Related Posts:
Tweet

Pin It