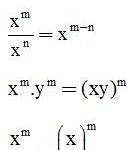Lý thuyết định lý Pytago và các dạng bài tập có lời giải từ A – Z

Trong bài viết dưới đây, chúng tôi sẽ giới thiệu lý thuyết về định lý Pytago thuận và định lý Pytago đảo và các dạng bài tập về định lý Pytago có lời giải chi tiết dưới đây để các bạn cùng tham khảo nhé

Nội Dung

Định lý Pytago

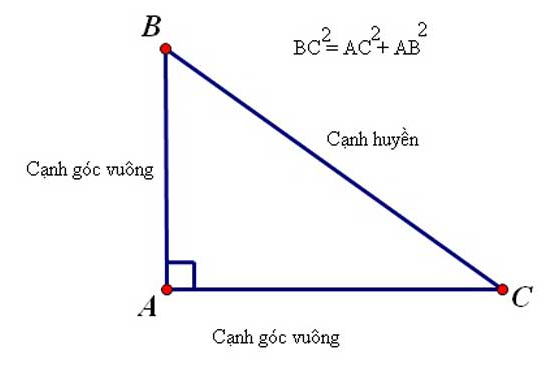
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

a² + b² = c²

Định lý Pytago đảo

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

ΔABC có BC² = AB² + AC²

⇒ ∠BAC = 90^o

Tham khảo thêm:

Bài tập ứng dụng định lý Pytago có lời giải

Ví dụ 1: Nếu độ dài của hai cạnh góc vuông của tam giác vuông tăng lên 2 lần, 3 lần thì độ dài cạnh huyền thay đổi như thế nào?

Gọi b, c là độ dài của cạnh góc vuông

a là độ dài cạnh huyền của tam giác vuông

Ta có: a² + b² = c²

Độ dài cạnh góc vuông tăng lên 2 lần

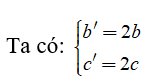
Khi đó ta có:

a’² = b’² + c’² = (2b)² + (2c)² = 4b² + 4c²

Hay a’² = 4(b + c)² = 4a² = (2a)²

Do đó cạnh huyền a’ tăng lên 2 lần (a’ = 2a)

Tương tự, khi độ dài cạnh góc vuông tăng lên 3 lần thì độ dài cạnh huyền cũng tăng lên 3 lần.

Ví dụ 2: Cho tam giác ABC vuông tại A. Gọi M là trung điểm của AB, kẻ MH vuông góc với BC tại H. Chứng minh rằng CH² – BH² = AC²

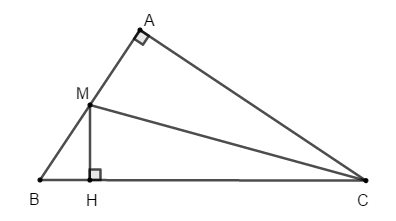
Lời giải

Nối C với M ta được tam giác vuông CMH

Áp dụng định lý Pytago ta có
CM² = CH² + MH²

⇒ CH² = CM² – MH²

Do đó:
CH² – BH² = (CM² – MH²) – BH²
= CM² – (MH² + BH²) = CM² – BM²
(do tam giác MBH vuông tại H nên MH² + BH² = BM²)

Mà MA = MB (do M là trung điểm của AB)

Nên CH² – BH² = CM² – MA² = AC² (do tam giác ACM vuông tại A)

Vậy CH² – BH² – AC²

Ví dụ 3: Một tam giác vuông có cạnh huyền bằng 26cm và có độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông?

Lời giải

Gọi độ dài các cạnh góc vuông lần lượt là x, y (x, y > 0)

Theo định lí Pytago ta có: x² + y² = 26² ⇔ x² + y² = 676

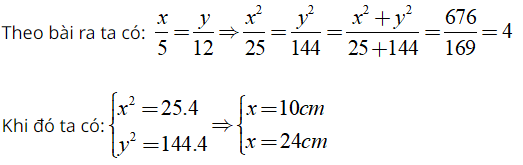
Ví dụ 4:Cho tam giác ABC vuông tại A có AC = 20cm. Kẻ AH vuông góc với BC. Biết BH = 9cm, HC = 16cm. Tính độ dài cạnh AB, AH?

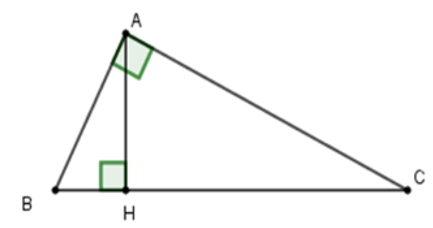
Lời giải

Ta có: BC = HB + HC = 9 + 16 = 25 (cm)

Xét tam giác ABC vuông tại A, theo định lí Pytago ta có:

BC² = AB² + AC² ⇒ AB² = BC² – AC² = 25² – 20² = 225 ⇒ AB = 15cm

Xét tam giác ABH vuông tại H, theo định lí Pytago ta có:

HB² + HA² = AB² ⇒ AH² = AB² – HB² = 15² – 9² = 144 ⇒ AH = 12cm

Vậy AH = 12cm, AB = 15cm

Ví dụ 5: Màn hình của một máy thu hình có dạng hình chữ nhật, chiều rộng 12 ich, đường chéo 20 ich. Tính chiều dài

Lời giải

Giả sử màn hình máy thu hình là hình chữ nhật ABCD, chều rộng BC = AD, chiều dài AB = CD, đường chéo AC = BD.

Ta có tam gác ABD vuông tại A

Theo định lý pytago ta có: BD²=AB²+AD²

⇒ AB² = BD² – AD² = 20²-12² = 400-144 = 256

Vậy AB = 16 ich

Ví dụ 6: Bạn An đi từ nhà mình (a) qua nhà bạn Lan (B) rồi đên nhà bạn Châu (C) . lúc trở về, An qua nhà bạn Dũng (D) rồi trở về nhà mình (hình bên). So sánh quãng đường lúc đi và quãng đường lúc về của An, quãng đường nào dài hơn.

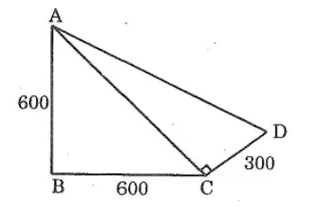
Lời giải

Trong tam giác vuông ABC có ∠ABC = 90^o
Áp dụng định lý pytago ta có:

AC²= AB²+ BC²= 600²+ 600²= 360000 + 360000 = 720000

Trong tam giác vuông ACD, ta có ∠ACD = 90^o

Áp dụng định lí pitago ta có:

AD² = AC² + CD² = 720000 + 300² = 720000 + 90000=810000

Suy ra: AD = 900m

Quãng đường ABC dài 600 + 600 = 1200m

Quãng đường CDA dài 300 + 900 = 1200m

Vậy quãng đường lúc đi và lúc về của An là bằng nhau

Bên trên là toàn bộ định lý Pytago và các dạng bài tập có lời giải có thể giúp các bạn nhớ được định lý để áp dụng vào làm bài tập đơn giản và chính xác nhé