Tam giác đều là gì ? Định nghĩa và tính chất của tam giác đều

Tam giác đều là gì ? Bạn đang gặp khó khăn khi học về tam giác đều ở trên lớp ? Tất cả thông tin sẽ được cập nhật về tam giác đều như : Định nghĩa, dấu hiệu nhận biết, tính chất, công thức tính diện tích, chu vi tam giác đều được cập nhật ở đây.

Tam giác đều là gì ?

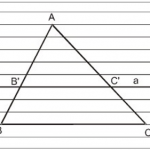
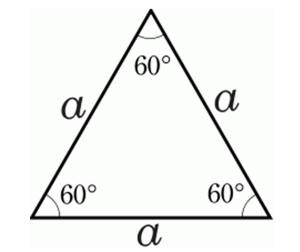
Trong hình học, tam giác đều là tam giác có ba cạnh bằng nhau hoặc tương đương ba góc bằng nhau, và bằng 60°. Nó là một đa giác đều với số cạnh bằng 3.

1. Định nghĩa tam giác đều

=> Tam giác đều là tam giác có 3 cạnh bằng nhau.

Hệ quả:

– Trong tam giác đều, mỗi góc bằng 60°
– Nếu trong một tam giác có ba góc bằng nhau thì đó là tam giác đều.
– Nếu một tam giác cân có 1 góc bằng 60° thì đó là tam giác đều.

2. Tính chất tam giác đều

• Tam giác có 3 cạnh bằng nhau là tam giác đều
• Tam giác có 3 góc bằng nhau là tam giác đều
• Tam giác cân có một góc bằng 60° là tam giác đều
• Tam giác có 2 góc bằng 60 độ là tam giác đều

3. Công thức tính điện tích tam giác đều

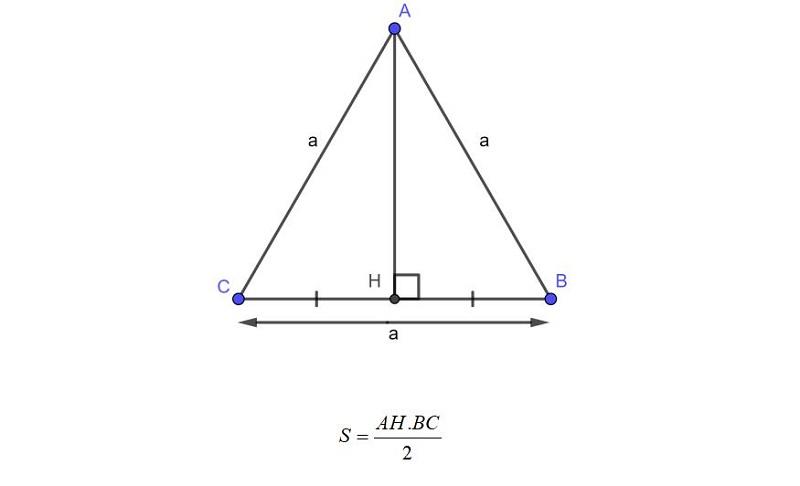
=> Diện tích tam giác đều bằng 1/2 tích của cạnh đáy nhân với chiều cao, công thức như sau S = 1/2 (a x h )

Trong đó

• S là diện tích tam giác
• a là độ dài cạnh đáy
• h là chiều cao

Ví dụ : Tính diện tích của tam giác đều có:

a, Độ dài một cạnh tam giác bằng 6cm và đường cao bằng 10cm

b, Độ dài một cạnh tam giác bằng 4cm và đường cao bằng 5cm

Lời giải

a, Diện tích hình tam giác là:

(6 x 10) : 2 = 30 (cm²)

Đáp số: 30cm²

b, Diện tích hình tam giác là:

(4 x 5) : 2 = 10 (cm²)

Đáp số: 10cm²

 

4. Công thức tính chu vi tam giác đều

=> Chu vi tam giác đều bằng tổng 3 cạnh của tam giác, công thức P = a + a + a  hoặc P = 3 x a

Trong đó

• P là chu vi tam giác đèu
• a là cạnh của tam giác

Ví dụ : Tính chu vi tam giác đều ABC với chiều dài cạnh AB = 5 cm

Lời giải:

=> Vì tam giác ABC là tam giác đều nên ta có, độ dài các cạnh là: AB = AC = BC = 5cm

+ Dựa vào công thức tính chu vi tam giác đều, ta có: P (ABC) = 5 x 3 = 15cm

Xem thêm :

1. Tính chất tam giác cân
2. Tính chất tam giác vuông
3. Diện tích tam giác