Công thức tính diện tích tam giác vuông, cân, đều kèm VD

Bạn muốn tính diện tích của mảnh đất hình tam giác nhưng bạn lại không nhớ công thức tính diện tích tam giác như thế nào? Chính vì vậy, THPT Chuyên Lam Sơn sẽ chia sẻ công thức tính diện tích tam giác thường, vuông, cân, đều kèm theo các dạng bài tập có lời giải chi tiết để các bạn cùng tham khảo

Nội Dung

1. Công thức tính diện tích tam giác thường

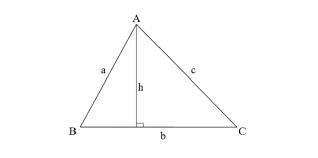
Diện tích tam giác được tính bằng ½ tích của chiều cao hạ từ đỉnh với độ dài cạnh đối diện của đỉnh đó. Nói cách khác, diện tích tam giác thường được tính bằng cách nhân chiều cao với độ dài đáy, sau đó tất cả chia cho 2

S = ½ h_a.a = ½ h_b.b= ½ h_c.c

Trong đó

S: là diện tích tam giác
a: độ dài cạnh đáy
h: chiều cao hạ từ đỉnh xuống đáy a

Ngoài ra, công thức tính diện tích tam giác khi biết 1 góc sẽ bằng ½ tích 2 cạnh kề với sin của góc hợp bởi 2 cạnh đó trong tam giác.

S = ½a.b.sinCˆ = ½a.c.sinBˆ = ½b.c.sinAˆ

Tính diện tích tam giác khi biết 3 cạnh bằng công thức Heron.

S = √p(p-a)(p-b)(p-c)

Với p là nửa chu vi tam giác:

p = ½ (a + b + c)

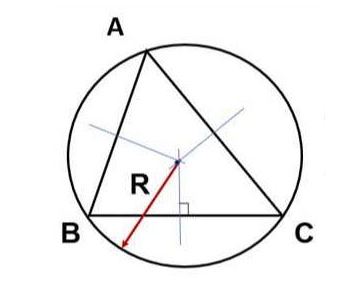
Tính diện tích bằng bán kính đường tròn ngoại tiếp tam giác (R).

S_ABC = abc/4R = 2R².sinÂ.sinBˆ.sinCˆ

Lưu ý: Cần phải chứng minh được R là bán kính đường tròn ngoại tiếp tam giác.

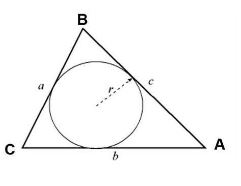
Tính diện tích bằng bán kính đường tròn nội tiếp tam giác (r).

S_ABC = p.r

Trong đó:

S là diện tích tam giác
p: Nửa chu vi tam giác.
r: Bán kính đường tròn nội tiếp.

Ví dụ 1: Một hình tam giác có đáy 15 cm và chiều cao 2,4cm. Tính diện tích hình tam giác đó?

Lời giải:

Diện tích hình tam giác là:

S = (15 x 2,4) : 2 = 18 (cm²)

Đáp số: 18cm²

Ví dụ 2: Một tấm bảng quảng cáo hình tam giác có tổng cạnh đáy và chiều cao là 28m, cạnh đáy hơn chiều cao 12m. Tính diện tích tấm bảng quảng cáo đó ?

Lời giải:

Độ dài cạnh đáy là:

a = (28 + 12) : 2 = 20 (m)

Độ dài chiều cao là:

h = 28 – 20 = 8 (m)

Diện tích tấm bảng quảng cáo là:

S = (20 x 8) : 2 = 80 (m²)

Đáp số: 80m²

Ví dụ 3: Cho tam giác ABC có diện tích bằng 40cm². Gọi M là trung điểm của AC . Tính diện tích tam giác ABM?

Lời giải

Gọi BH là đường cao ứng với cạnh Ac

Diện tích tam giác ABC là

S_ABC = ½BH.AC = 40

Do M là trung điểm của Ac nên

AM = MC = ½AC

Diện tích tam giấc ABM là

S_ABM = ½BH.AM = ½BH.½AC = ½S_ABC = ½.40 = 20cm²

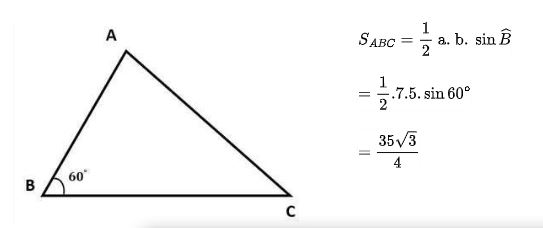
Ví dụ 4: Tam giác ABC có cạnh BC = 7, cạnh AB = 5, góc B bằng 60 độ. Tính diện tích tam giác ABC?

Lời giải

Ví dụ 5: Cho tam giác ABC, độ dài các cạnh a = 6, b = 7, c = 5, R = 3 (R là bán kính đường tròn ngoại tiếp tam giác ABC). Tính diện tích của tam giác ABC.

Lời giải

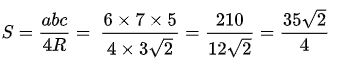
2. Công thức tính diện tích tam giác đều

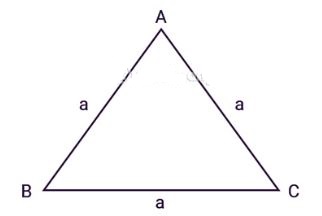
Tam giác đều là tam giác có 3 cạnh bằng nhau và tất cả các góc trong tam giác đều bằng 60 độ. Trong đó cách tính diện tích tam giác đều cũng tương tự cách tính tam giác thường, chỉ cần bạn biết chiều cao tam giác và cạnh đáy. Do đó, diện tích tam giác đều được tính bằng công thức nhau sau:

S = ½. A². sin 60^o = A².√3/4

Trong đó

A là cạnh của tam giác đều.
S là diện tích tam giác

Xem ngay: Tam giác đều là gì ? Định nghĩa và tính chất của tam giác đều

Bài tập ví dụ : Cho tam giác ABC đều, cạnh a=4(cm). Tinh diện tích tam giác ABC.

Lời giải

Xét △ABC đều

Ta áp dụng công thức tính diện tích hình tam giác đều, suy ra S_△ABC=a².√3/4=4².√3/4 = 4√3 (cm²)

Ví dụ 2: Tính diện tích tam giác đều ABC ngoại tiếp đường tròn (I; r)

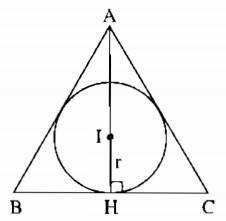
Lời giải

Gọi H là tiếp điểm của đường tròn (I) với BC.

Ta có: IH⊥BC (tính chất tiếp tuyến)

Vì I là tâm đường tròn nội tiếp tam giác ABC nên AI là tia phân giác của BACˆ

Tam giác ABC đều nên AI cũng là đường cao của △ABC. Khi đó A, I, H thẳng hàng.

Ta có: HB=HC ( tính chất tam giác đều)

Tam giác ABC đều nên I cũng là trọng tâm của △ABC.

Suy ra: AH=3.HI=3.r

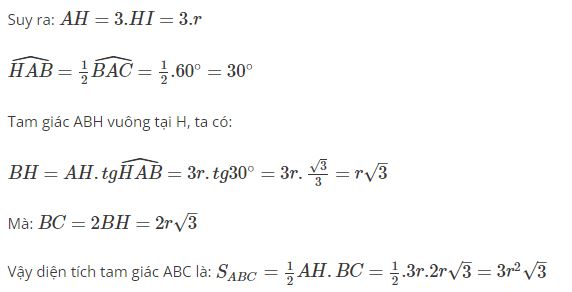
3. Công thức tính diện tích tam giác vuông

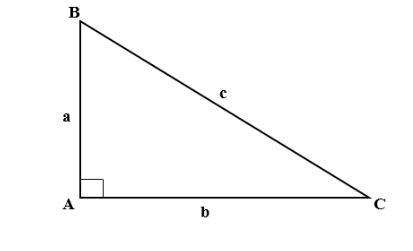
Công thức tính diện tích tam giác vuông tương tự như cách tính diện tích tam giác thường đó là bằng ½ tích của chiều cao với chiều dài đáy.

S = ½ a.b

Trong đó

S là diện tích tam giác vuông
a là chiều cao tam giác
b là cạnh đáy

THam khảo thêm: Tam giác vuông là gì ? Định nghĩa và tính chất của tam giác vuông

Chú thích : Vì tam giác vuông là tam giác có hai cạnh góc vuông nên chiều cao của tam giác sẽ ứng với một cạnh góc vuông và chiều dài đáy ứng với cạnh góc vuông còn lại.

Ví dụ: Cho tam giác ABC vuông góc tại B, chu vi là 37dm. Cạnh AB bằng 2/3 cạnh AC, cạnh BC bằng 4/5 cạnh AC. Tính diện tích hình tam giác ABC ?

Lời giải

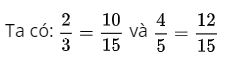
Cạnh AC là 15 phần bằng nhau thì cạnh AB là 10 phần và BC là 12 phần như thế.

Độ dài cạnh AB là:

37 : (15 + 10 + 12) x 10 = 10 (dm)

Độ dài cạnh AC là:

37 : (15 + 10 + 12) x 15 = 15 (dm)

Độ dài cạnh BC là:

37 – 10 – 15 = 12 (dm)

Diện tích hình tam giác ABC là:

10 x 12 : 2 = 60 (dm²)

Đáp số: 60dm²

Ví dụ 2: Cho tam giác ABC vuông góc tại A, chu vi là 90cm. Cạnh AB bằng 4/3 cạnh AC, cạnh BC bằng 5/3 cạnh AC. Tính diện tích hình tam giác ABC ?

Giải:

Cạnh AC là 3 phần bằng nhau thì cạnh AB là 4 phần và cạnh BC là 5 phần như thế

Độ dài cạnh AB là:

90 : (3 + 4 + 5) x 4 = 30 (cm)

Độ dài cạnh AC là:

90 : (3 + 4 + 5) x 3 = 22,5 (cm)

Diện tích hình tam giác ABC là:

30 x 22,5 : 2 = 337,5 (cm²)

Đáp số: 337,5 cm²

Tính diện tích tam giác vuông cân

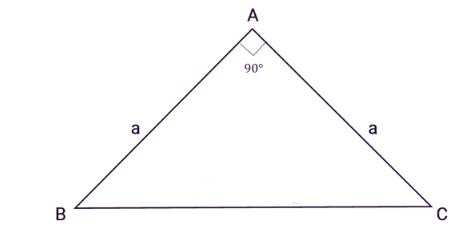
Tam giác ABC vuông cân tại A, a là độ dài hai cạnh góc vuông. Khi đó 2 cạnh góc vuông sẽ bằng nhau và diện tích tam giác vuông cân sẽ được tính bằng ½ bình phương độ dài cạnh góc đáy

S = ½ a²

Trong đó:

S là diện tích tam giác
a chính là độ dài của cạnh góc vuông cân.

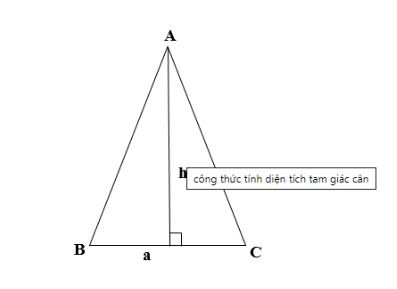
4. Cách tính diện tích tam giác cân

Diện tích tam giác cân sẽ được tính bằng một nửa chiều cao nhân cạnh đáy tương ứng chiếu lên.

S = ½h.a

Trong đó :

S là diện tích tam giác
a là cạnh đáy
h là đường cao

Tham khảo thêm: Tam giác cân là gì ? Định nghĩa và tính chất tam giác cân

Bài tập ví dụ : Tính diện tích của tam giác cân có:

a, Độ dài cạnh đáy bằng 6cm và đường cao bằng 7cm

b, Độ dài cạnh đáy bằng 5m và đường cao bằng 3,2m

Lời giải:

a, Diện tích của hình tam giác là:

(6 x 7) : 2 = 21 (cm²)

Đáp số: 21cm²

b, Diện tích của hình tam giác là:

(5 x 3,2) : 2 = 8 (m²)

Đáp số: 8m²

Sau khi đọc xong bài viết của chúng tôi có thể giúp các bạn nhớ được các công thức tính diện tích tam giác thường, vuông, cân, đều để áp dụng vào làm bài tập nhanh chóng nhé.