Định nghĩa và công thức tính diện tích, thể tích hình chóp lục giác đều kèm VD minh họa
Hình chóp lục giác là một hình học đặc biệt trong cấu trúc hình học, được coi là hình có diện tích các cạnh nhỏ nhất nhưng lại phủ chứa được lượng không gian lớn nhất và hình chóp lục giác là hình được ứng dụng khá rộng rãi trong tính toán thực tế. Chúng ta sẽ tìm hiểu công thức tính toán này trong bài viết ngay dưới đây của chúng tôi nhé
Tham khảo thêm:
- Định nghĩa diện tích, thể tích của chóp tứ giác đều kèm bài tập có lời giải
- Định nghĩa hình chóp cụt là gì? Công thức tính diện tích, thể tích hình chóp cụt kèm ví dụ có lời giải
- Đinh nghĩa và công thức tính diện tích, thể tích lăng trụ tam giác đều 100%
Nội Dung
Hình chóp lục giác đều là gì?
Hình chóp lục giác đều là hình chóp có đáy là một lục giác đều và đường cao đi qua tâm đáy
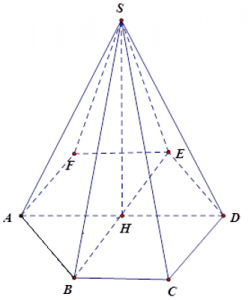
Tính chất:
- Các mặt bên bằng nhau
- Các mặt bên là tam giác cân tại đỉnh
- Cạnh bên bằng nhau
- Cạnh đáy bằng nhau
- Khoảng cách tâm đáy đến cách điểm đều bằng nhau
- Các cạnh đáy bằng bán kính đường tron ngoại tiếp
Công thức tính thể tích hình chóp lục giác đều
Thể tích hình chóp lục giác đều là 1/3 diện tích đáy nhân chiều cao
V= 1/3. Sđáy. h
Trong đó:
- V: Thể tích chóp lục giác đều
- Sđáy: Diện tích đáy chóp lục giác đều
- h: Chiều cao chóp lục giác đều
Chú ý: Diện tích lục giác đều là: (3√3 ( cạnh)2) / 2
Công thức tính diện tích xung quanh hình chóp lục giác đều
Diện tích xung quanh của hình chóp lục giác đều là tích nửa chu vi đáy với trung đoạn
Sxq= P/2. d
Trong đó:
- Sxq: Diện tích xung quanh
- P/2: Nửa chu vi của đáy lục giác đều
- d: Trung đoạn của lục giác đều
Chú ý: Chu vi lục giác đều là: Pcác mặt bên + Pmặt đáy
Công thức tính diện tích toàn phần hình chóp lục giác đều
Diện tích toàn phẩn hình chóp lục giác đều là tổng của diện tích xung quanh và diện tích đáy
Stp= Sxq + Sđáy
Trong đó:
- Stp: Diện tích toàn phần của hình chóp lục giác đều
- Sxq: Diện tích xung quanh của hình chóp lục giác đều
- Sđáy: Diện tích đáy của chóp lục giác đều
Các dạng tập của hình chóp lục giác đều
Bài tập 1: Tính thể tích V của khối chóp lục giác đều có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy băng 30 độ. Thể tích khối chóp bằng
Bài giải:
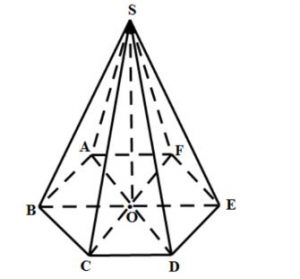
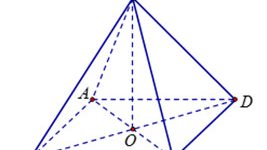
Đặt S.ABCDEF hình chóp lục giác đều ABCDEF là hình chóp thảo mãn đề bài
Gọi O là tâm của ABCDEF
⇒OA = OB = OC = OE = OF = AB = BC = CD = DE = EF = FA = a
⇒ Tam giác OAB đều cạnh a
⇒ S.ABCDEF = 6 SOAB

Bài tập 2:Cho hình chóp lục giác đều S.ABCDEF có cạnh đáy bằng 6cm, cạnh bên bằng 12cm. Tính diện tích xung quanh hình chóp.
Bài giải:
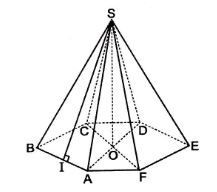
Gọi I là trung điểm cạnh AB. Trong tam giác vuông SIA,ta có:
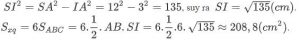
Bài tâp 3: Hình chóp lục giác đều S.ABCDEH có AB = 6cm, cạnh bên SA = 10cm. Vậy chiều cao hình chóp là
Bài giải:
Gọi SO là đường cao của hình chóp.
Khi đó ∆ AOB là tam giác đều có cạnh AB = 6cm ⇒ OA = 6(cm).
Trong tam giác vuông SOA, áp dụng định lí Pi-ta-go ta tính được SO = 8(cm).
Bài tập 4: Tính diện tích xung quanh và thể tích của hình chóp lục giác đều có cạnh đáy là 5 cm và đường cao là 9 cm
Bài giải:
Lục giác chia thành 6 tam giác bằng nhau, vậy diện tích của một tam giác là:
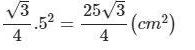
Diện tích lục giác đều là:
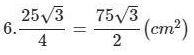
Thể tích chóp lục giác đều là:
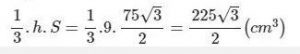
Bài 5: S.MNOPQR là một hình chóp lục giác đều (h.132). Bán kính đường tròn ngoại tiếp đáy (đường tròn tâm H, đi qua sáu đỉnh của đáy) HM = 12cm (h.133), chiều cao SH = 35cm. Hãy tính:
a) Diện tích đáy và thể tích của hình chóp (biết √108 ≈ 10,39);
b) Độ dài cạnh bên SM và diện tích toàn phần của hình chóp (biết √1333 ≈ 36,51).
Giải:
a) Tam giác HMN là tam giác đều. Đường cao là :
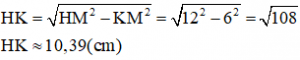
Diện tích đáy của hình chóp lục giác đều chính là 6 lần diện tích của tam giác đều HMN. Nên:
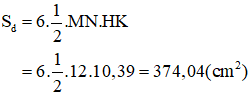
Thể tích của hình chóp:

Diện tích xung quanh của hình chóp là:

Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình