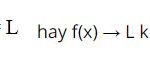Nhân đơn thức với đa thức là gì? Quy tắc nhân đơn thức với đa thức và bài tập có lời giải chính xác 100%

Nhân đơn thức với đa thức giúp bạn giải các bài tập trong sách giáo khoa toán, học tốt toán cấp 2 sẽ giúp bạn rèn luyện khả năng suy luận hợp lý và hợp logic, hình thành khả năng vận dụng kết thức toán học vào đời sống và vào các môn học khác

Tham khảo thêm:

Nội Dung

Quy tắc nhân đơn thức với đa thức

Muốn nhân một đơn thức với một đa thức ta nhân đơn thức với từng số hạng của đa thức rồi cộng các tích với nhau.

Công thức: Cho A, B, C là các đơn thức ta có: A( B + C)= AB+ AC

Nhắc lại các phép tính về lũy thừa.

a ⁿ = a.a…a (a ∈ Q, n N* ) ( n thừa số a)

a ⁰= 1 ( a ≠ 0 )

aⁿ.a ^m= a ^n-m ( n ≥.m)

(a ^m) ⁿ = a ^m.n

Các dạng bài tập nhân đa thức với đơn thức có lời giải

Dạng 1: Thực hiện phép tính (hoăc rút gọn biểu thức)

Phương pháp: sử dụng quy tắc nhân đơn tức với đa thức

Ví dụ 1: Thực hiện các phép tính sau:

a, Ta có: x²(x+y)+2x(x²+y)

=x².x+x².y+2x.x²+2x.y

=x³+x²y+2x³+2xy

=3x³+x²y+2xy

b, Ta có : ( x² + 2xy – 3 ).( – xy )

= x².( – xy ) + 2xy.( – xy ) – 3.( – xy )

= – x³y – 2x²y² + 3xy

c, Ta có: 1/2 x²(6x – 3) – x( x² + 1/2 (x + 4)

= 3x³ – 3/2 x² – x³ – 1/2 x + 1/2 x + 2

= 2x³ – 3/2 x² + 2

Dạng 2: Tìm x

Phương pháp: Sử dụng các quy tắc nhan đơn thức với đa thức để biến đổi về dạng tìm x cơ bản

Ví dụ 1: Tìm x biết

a, Ta có 4( 18 – 5x ) – 12( 3x – 7 ) = 15( 2x – 16 ) – 6( x + 14 )

⇔ 4.18 – 4.5x – 12.3x – 12.( – 7 ) = 15.2x – 15.16 – 6.x – 6.14

⇔ 72 – 20x – 36x + 84 = 30x – 240 – 6x – 84

⇔ 156 – 56x = 24x – 324

⇔ 56x + 24x = 156 + 324

⇔ 80x = 480

⇔ x = 6.

Vậy giá trị x cần tìm là x = 6.

b, Ta có 2( 5x – 8 ) – 3( 4x – 5 ) = 4( 3x – 4 ) + 11

⇔ 2.5x – 2.8 – 3.4x – 3.( – 5 ) = 4.3x – 4.4 + 11

⇔ 10x – 16 – 12x + 15 = 12x – 16 + 11

⇔ – 2x – 1 = 12x – 5 ⇔ 12x + 2x = – 1 + 5

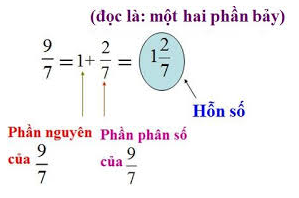
⇔ 14x = 4 ⇔ x = 2/7.

Dạng 3: Tính giá trị biểu thức

Phướng pháp: Giá trị của biếu thức f(x) tại x₀ là f (x₀)

Ví dụ: Rút gọn rồi tính giá trị biểu thức: A= 5x (x − 4y) − 4y (y − 5x) với x = − 1/5; y = − 1//2

Ta có: A = 5x (x − 4y) − 4y (y − 5x)

⇔ A = 5x. x − 5x.4y − 4y. y − 4y (−5x)

⇔ A = 5x² − 20xy − 4y² + 20xy

⇔ A = 5x² − 4y²

Tại x = -1/5 và y = -1/2 ta có:

A= 5 (-1/5)² – 4 (-1/2)²

= 5. 1/25 – 4. 1/4

= 1/5 – 1

= -4/5

b, Ta có: P = 5x(x² – 3) + x²(7 – 5x) – 7x²

= 5x³ – 15x + 7x² – 5x³ – 7x² = – 15x

Thay x = -5 vào P = -15x ta được: P = – 15.(-5) = 75

Vậy giá trị x cần tìm là x = 2/7

c,Ta có: P = 5x(x² – 3) + x²(7 – 5x) – 7x²

= 5x³ – 15x + 7x² – 5x³ – 7x² = – 15x

Thay x = -5 vào P = -15 ta được: P = – 15.(-5) = 75

Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình