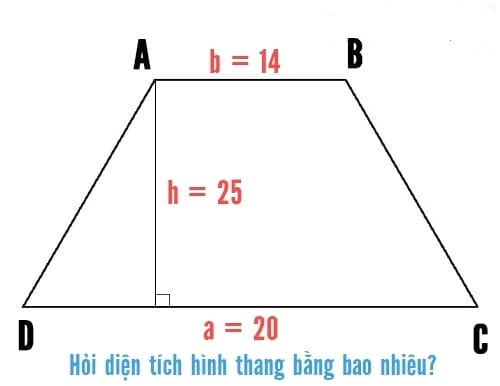
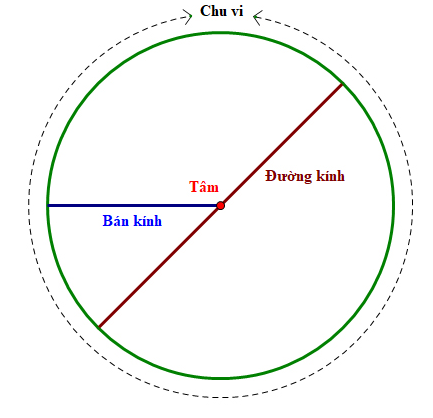
Định Lý và Công thức Sin Cos Tan lớp 9, lớp 10, lớp 11, lớp 12

Hiện nay có rất nhiều các bạn học sinh không nắm chắc được các công thức sin cos tan và định lý sin cos trong tam giác, hình học hay trong hàm lượng giác trong toán lớp 9, lớp 10, lớp 11, lớp 12….Chính vì vậy, THPT Chuyên Lam Sơn sẽ chia sẻ định lý sin cos trong tam giác kèm theo các bạn bài tập có lời giải để các bạn cùng tham khảo

Nội Dung

1. Định lý hàm Sin

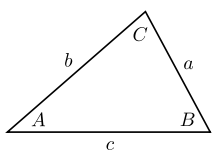
Trong lượng giác, định lý sin (hay định luật sin, công thức sin) là một phương trình biểu diễn mối quan hệ giữa chiều dài các cạnh của một tam giác bất kì với sin của các góc tương ứng. Định lý sin được biểu diễn dưới dạng.

a/sinA = b/sinB = c/sinC = 2R

Trong đó a, b, c là chiều dài các cạnh, và A, B, C là các góc đối diện (xem hình vẽ). Phương trình cũng có thể được viết dưới dạng nghịch đảo:

sinA/a = sinB/b = sinC/c

Định lý sin có thể được dùng trong phép đạc tam giác để tìm hai cạnh còn lại của một tam giác khi biết một cạnh và hai góc bất kì, hoặc để tìm cạnh thứ ba khi biết hai cạnh và một góc không xen giữa hai cạnh đó.

Trong một vài trường hợp, công thức cho ta hai giá trị khác nhau, dẫn đến hai khả năng khác nhau của một tam giác.

Định lý hàm sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

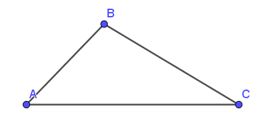
Ví dụ: Cho tam giác nhọn ABC có BC = 8cm, AB = 7cm và ˆA = 60^o. Tính số đo góc ˆC
.

Lời giải

Xét tam giác nhọn ABC

Áp dụng định lí Sin ta có:

BC/sinA = AB/sinC

⇒sinC = (AB.sinA)/BC

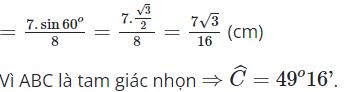
2. Định lý hàm Cos trong tam giác

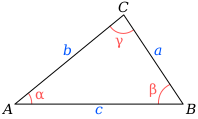
Trong một tam giác, bình phương một cạnh bằng tổng của hai cạnh kia trừ đi hai lần tích của chúng với cosin của góc xen giữa hai cạnh đó.

c² = a² + b² – 2abcosγ hoặc c² = a² + b² – 2abcos C

⇒

Định lý hàm cos khái quát định lý Pytago (định lý Pytago là trường hợp riêng trong tam giác vuông): nếu γ là góc vuông thì cos γ = 0, và định lý cos trở thành định lý Pytago:

c² = a² + b²

Định lý hàm cos được dùng để tính cạnh thứ ba khi biết hai cạnh còn lại và góc giữa hai cạnh đó, hoặc tính các góc khi chỉ biết chiều dài ba cạnh của một tam giác.

a² = b² + c² – 2bccosα

b² = a² + c² – 2accosβ

Ví dụ 1: Đường dây cao thế thẳng từ A đến B có độ dài 10km, từ A đến C có độ dài 8km, góc tạo bởi hai đường dây trên khoảng 75 độ. Tỉnh khoảng cách từ B đến C?

Lời giải:

Theo định lý cos ta có:

a²=b²+c²-a.b.c.cosA= 8² + 10² -2.8.10.cos75 = 11 km

Khoảng cách giữa B và C là 11 km

Ví dụ 2:

Cho tam giác ABC có BC = a, CA = b, AB = c và đường trung tuyến AM = c = AB. Chứng minh rằng: a²=2(b²+c²)

Lời giải:

Ta có định lý về trung tuyến như sau:

AM²=2(AB²+AC²)- BC24

c²=2(c²+b²)-a24

4c²=2c²+2b²–a²

a²=2(b²–c²) (dpcm)

3. Công thức Sin Cos Tan trong lượng giác

Ngày nay, chúng ta thường làm việc với sáu hàm lượng giác cơ bản, được liệt kê trong bảng dưới, kèm theo liên hệ toán học giữa các hàm.

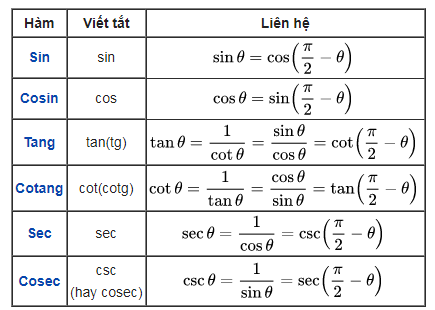
Xem thêm : Công thức lượng giác

4. Sin Cos Tan trong tam giác vuông

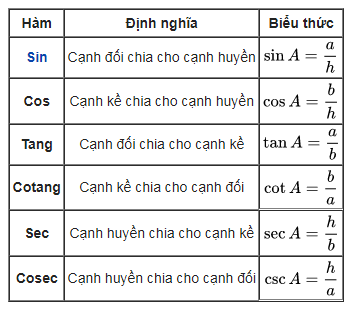
Có thể định nghĩa các hàm lượng giác của góc A, bằng việc dựng nên một tam giác vuông chứa góc A. Trong tam giác vuông này, các cạnh được đặt tên như sau:

Cạnh huyền là cạnh đối diện với góc vuông, là cạnh dài nhất của tam giác vuông, h trên hình vẽ.
Cạnh đối là cạnh đối diện với góc A, a trên hình vẽ.
Cạnh kề là cạnh nối giữa góc A và góc vuông, b trên hình vẽ.

Dùng hình học Ơclit, tổng các góc trong tam giác là pi radian (hay 180⁰). Khi đó:

5. Sin Cos Tan trong hình học

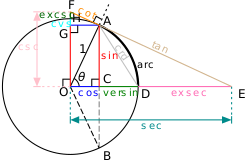
Hình vẽ bên cho thấy định nghĩa bằng hình học về các hàm lượng giác cho góc bất kỳ trên vòng tròn đơn vị tâm O. Với θ là nửa cung AB:

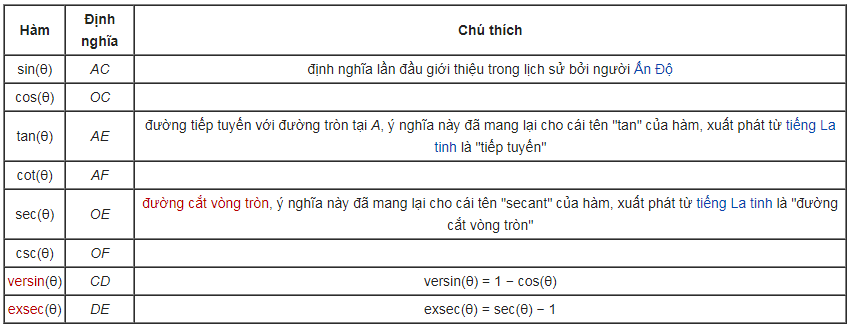
Theo hình vẽ, dễ thấy sec và tang sẽ phân kỳ khi θ tiến tới π/2 (90 độ), cosec và cotang phân kỳ khi θ tiến tới 0. Nhiều cách xây dựng tương tự có thể được thực hiện trên vòng tròn đơn vị, và các tính chất của các hàm lượng giác có thể được chứng minh bằng hình học.