Hai góc đối đỉnh là gì? Tính chất và bài tập có đáp án cực hay

Tiếp tục ở chuyên mục Toán Học hôm nay, THPT CHUYÊN LAM SƠN chia sẻ lý thuyết hai góc đối đỉnh là gì? Tính chất của hai góc đối đỉnh kèm theo các bài toán thường gặp có lời giải chi tiết trong bài viết dưới đây để các bạn cùng tham khảo

• Tham khảo thêm: Lý thuyết hàm số và phương pháp giải bài tập có lời giải từ A – Z

Định nghĩa hai góc đối đỉnh

Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia

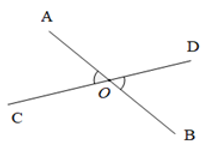
Ví dụ: Trong hình vẽ dưới đây thì ∠AOC và ∠BOD là hai góc đối đỉnh

Tính chất của hai góc đối đỉnh

• Hai góc đối đỉnh thì bằng nhau.

Ví dụ: Ta chứng minh hai góc O₁ và O₃ bằng nhau

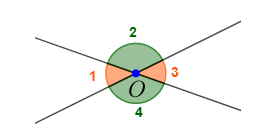
Vì hai góc O₁ và O₂ kề bù nên: O^∧₁ + O^∧₂ = 180⁰ (1)

Vì hai góc O₃ và O₂ kề bù nên: O^∧₃ + O^∧₂ = 180⁰ (2)

Từ (1) và (2) ta có: O^∧₁ + O^∧₂ = O^∧₃ + O^∧₂

Suy ra O^∧₁ = O^∧₃

Cặp góc đối đỉnh O₂ và O₄ cũng được chứng minh hoàn toàn tương tự

Bài tập về hai góc đối đỉnh thường gặp

Dạng 1: Xác định các cặp góc đối đỉnh theo yêu cầu bài toán

Phương pháp: Vẽ hình và xác định các cặp góc đối đỉnh theo định nghĩa

Ví dụ 1: Vẽ hai đường thằng zz’ và tt’ cắt nhau tại A. Hãy viết tên hai cặp góc đối đỉnh.

Lời giải

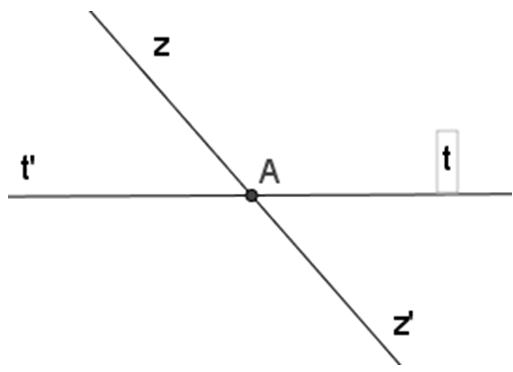
Cặp góc đối đỉnh thứ nhất là góc zAt’ và góc z’At (vì Az và Az’; At’ và At là các cặp tia đối nhau).

Cặp góc đối đỉnh thứ hai là góc zAt và z’At’ (vì Az và Az’; At và At’ là các cặp tia đối nhau)

Ví dụ 2: Ba đường thẳng xx’, yy’, zz’ cùng đi qua điểm O. Hãy viết tên các cặp góc bằng nhau.

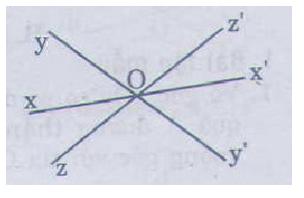
Lời giải

Trên hình vẽ ba đường thẳng xx’, yy’, zz’ cùng đi qua điểm O.

Tên các cặp góc bằng nhau là:

xOy = x’Oy’; yOz = y’Oz’
zOx = z’Ox’; xOz = x’Oz’
yOx’ = y’Ox; zOy’ = z’Oy
xOx’ = yOy’ = zOz’

Dạng 2: Tính số đo góc. Xác định các cặp góc bằng nhau

Phương pháp: Sử dụng tính chất của hai góc đối đỉnh và các tính chất sau:

• Hai góc bù nhau thì có tổng số đo bằng 180⁰
• Hai góc kề nhau có tổng số đo bằng 180⁰

Ví dụ 1: Vẽ hai đường thẳng cắt nhau sao cho trong các góc tạo thành có một góc 47^o. Tính số đo các góc còn lại

Lời giải

Vẽ hình:

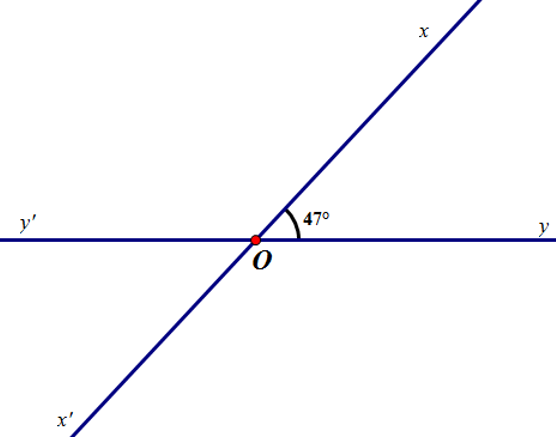
Vẽ đường thẳng xx’.

Trên đường thẳng xx’ ta lấy điểm O bất kì.

Sử dụng thước đo góc để vẽ tia yy’ đi qua O sao cho góc xOy = 47º.

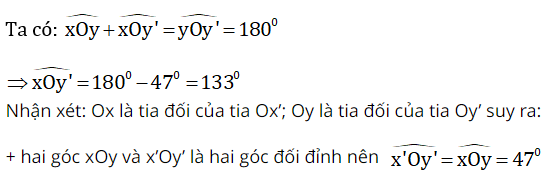
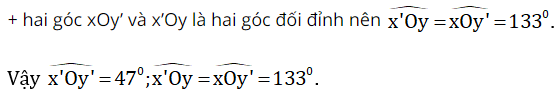
Ví dụ 2: Cho hai đường thẳng xy và zt cắt nhau tại O. Biết rằng ∠xOt lớn gấp 4 lần góc ∠xOz. Tính các góc ∠xOt, ∠tOy, ∠xOz, ∠yOz ?

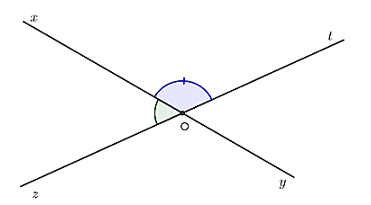
Lời giải

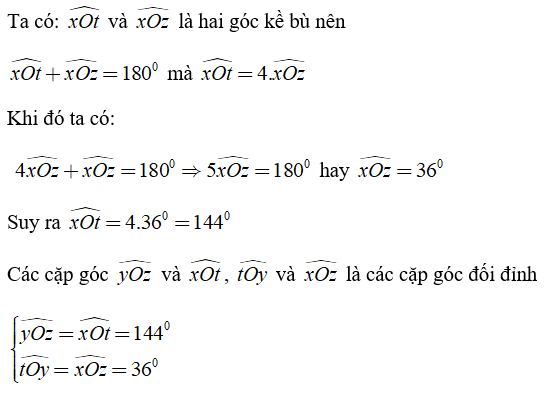
Bên trên chính là toàn bộ lý thuyết hai góc đối đỉnh và phương pháp giải bài tập về hai góc đối đỉnh có thể giúp các bạn áp dụng vào làm bài tập chính xác và đơn giản