Đinh nghĩa và công thức tính diện tích, thể tích lăng trụ tam giác đều 100%

Trong bài viết dưới đây, chúng tôi sẽ chia sẻ tới các bạn kiến thức về lăng trụ tam giác đều bao gồm: định nghĩa, tính chất, diện tích xung quanh, diện tích toàn phần và thể tích giúp các bạn củng cổ lại kiến thức để vận dụng giải các bài tập

Tham khảo thêm:

• Số thực là gì? Tính chất của số thực và bài tập chi tiết từ A – Z
• Hỗn số là gì? Cách chuyển đổi của hỗn số và bài tập chính xác 100%
• Số hữu tỉ là gì? Cách so sánh số hữu tỉ và bài tập có lời giải từ A – Z

Lăng trụ tam giác đều là gì?

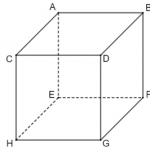
Hình lăng trụ tam giác đều là hình lăng trụ có hai đáy là hai tam giác đều bằng nhau.

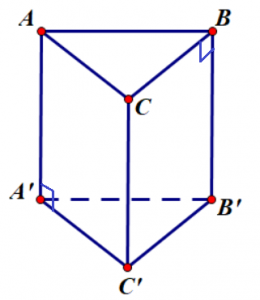
Tính chất:

• Một đa diện gồm có hai đáy là hai đa giác bằng nhau
• Cằm trên hai mặt phẳng song song,
• Các mặt bên là hình bình hành,
• Các cạnh bên song song hoặc bằng nhau

Công thức tính thể tích của một lăng trụ tam giác đều

Thể tích hình lăng trụ bằng diện tích của mặt đáy và khoảng cách giữa hai mặt đáy hoặc là chiều cao. Công thức tính thể tích hình lăng trụ tam giác giác đều

V=B.h

Trong đó:

• B là diện tích đáy,
• H là chiều cao của khối lăng trụ
• V là thể tích khối lăng trụ

Chú ý: Diện tích tam giác đều là: ( cạnh )²       

Công thức tính diện tích xung quanh lăng trụ tam giác đều

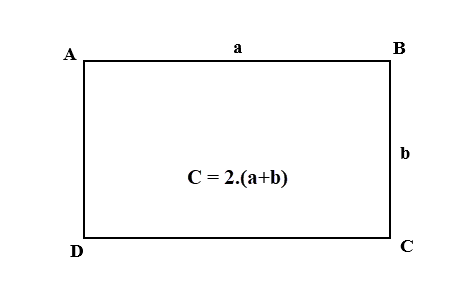
Diện tích xung quanh lăng trụ tam giác đều bằng tổng diện tích các mặt bên hoặc bằng chu vi đáy nhân với chiều cao

S_xq= P. h

Trong đó:

• P: chu vi đáy.
• h: chiều cao

Công thức tính diện tích toàn phần lăng trụ tam giác đều

Diện tích toàn phần của lăng trụ tam giác đều bằng tổng diện tích các mặt bên và diện tích 2 đáy

S_tp =  S_xq + 2S_đáy

Trong đó:

S_tp: Diện tích toàn phần của lăng trụ tam giác đều

S_xq: Diện tích xung quanh của lăng trụ tam giác đều

2S_đáy: Diện tích 2 đáy của lăng trụ tam giác đều

Các dạng bài tập về lăng trụ tam giác đều

Bài tập 1. Cho hình lăng trụ tam giác đều ABC.A’B’C’. Hãy tính thể tích khối lăng trụ này

a) AB = 2 cm; AA’ = 6 cm

b) AB = 6 cm; BB’ = 8 cm

c) BC = 3,5 cm; CC’ = 6 cm

a, Theo giải thiết ta có:

• a = AB = 2 cm
• h = AA’ = 6 cm

Áp dụng công thức tính thể tích lăng trụ tam giác đều:

V = h. a² . 3√4 = 6. 22 .3√4 = 63–√(cm³)

b,Theo đề bài tao có:

• a = AB = 6 cm
• h = BB’ = 8 cm

Áp dụng công thức tính thể tích khối lăng trụ tam giác đều:

V = h . a² . 3√4 = 8 . 62 . 3√4 = 723–√(cm³)

c, Theo giải thiết tao có:

• a = BC = 3,5 cm
• h = CC’ = 6 cm

Sử dụng công thức tính thể tích lăng trụ tam giác đều:

V = h . a² . 3√4 = 6. 3,52 . 3√4= 31,83 (cm³)

Bài tập 2: Tính thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a.

Giải:

Khối lăng trụ của đáy là tam giác đều cạnh a, chiều cao h=a.

Nên suy ra có thể tích là: V = S_đáy . h = a²3 √4 .a = a³3√4

Bài tập 3: Tính thể tích khối trụ tam giác đều ABCA’B’C’ có độ dài cạnh đáy bằng 8cm và mặt phẳng A’B’C’ tạo với mặt đáy ABC một góc bằng 60 độ.

Giải:

Gọi I là trung điểm của đoạn thẳng BC ta có:

AI vuông góc BC (theo tính chất đường trung tuyến của một tam giác đều)

A’I vuông góc BC (Vì A’BC là tam giác cân)

Góc A’BC, ABC = góc AIA’ = 60 độ

Diện tích tam giác ABC là:

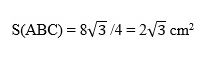
Thể tích khối lăng trụ tam giác đều ABCA’B’C’ là:

Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình