Căn bậc hai là gì? Công thức tính căn bậc hai kèm bài tập từ cơ bản đến nâng cao
Trong toán học, căn bậc 2 là phần kiến thức trọng yếu, bạn bắt buộc phải nắm được những kiến thức cơ bản về mảng này để tránh gặp phải những sai sót không đáng. Tuy nhiên, nếu để học một lần hết tất cả các kiến thức về căn bậc 2 là điều không khả thi. Vậy nên, phần kiến thức này được nâng cấp dần dần qua các năm học. Bạn đã học được một vài phần về căn bậc 2 ở lớp 7 rồi, vậy với phần căn bậc hai lớp 9 này, bạn sẽ được bổ sung thêm kiến thức gì?
Tham khảo thêm:
- Phân tích đa thức thành nhân tử chung và bài tập có lời giải từ A- Z
- Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp và bài tập có lời giải
- Rút gọn phân số là gì? Khái niệm rút gọn phân số và bài tập có lời giải chính xác 100%
Nội Dung
Căn bậc hai là gì?
Căn bậc hai số học của số thực a không âm là số không âm x mà x2 = a. Với a ≥ 0
Tính chất:
- Số âm không có căn bậc hai
- Số 0 có đúng một căn bậc hai đó chính là số 0, ta viết √0 = 0
- Số dương a có đúng hai căn bậc hai là hai số đối nhau; số dương ký hiệu là √a, số âm ký hiệu là -√a
Căn bậc hai số học là gì?
Với số dương a, số √a được gọi là căn bậc hai số học của a. Còn với số 0 cũng được gọi là căn bậc hai số học của 0.
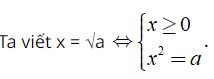
Phép khai phương của căn bạc hai :
Phép khai phương là phép toán tìm căn bậc hai số học của số không âm (gọi tắt là khai phương). Khi biết một căn bậc hai số học của một số, ta dễ dàng xác định được các căn bậc hai của nó.
+) Với A ≥ 0, B ≥ 0 thì √(A.B) = √A . √B và ngược lại √A . √B = √(A.B)
Đặc biệt, khi A ≥ 0, ta có:
![]()
+) Với A ≥ 0, B > 0 thì:

Một số kết quả cần nhớ :
- Với a ≥ 0 thì a = (√a)2.
- Với a ≥ 0, nếu x ≥ 0 và x2 = a thì x = √a.
- Với a ≥ 0 và x2 = a thì x = ±√a.
Cách biến đổi biểu thức chứa căn bậc hai
+) Đưa thừa số ra ngoài dấu căn:
![]()
+) Đưa thừa số vào trong dấu căn:
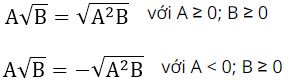
+) Khử mẫu ở biểu thức chứa căn:
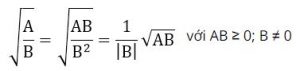
+) Trục căn thức ở mẫu:
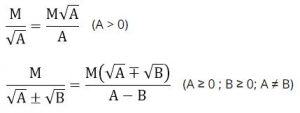
Cách tút gọn biểu thức có chứa căn bậc hai
- Bước 1: Dùng các phép biến đổi đơn giản để đưa các căn thức bậc hai phức tạp thành căn thức bậc hai đơn giản.
- Bước 2: Thực hiện các phép tính theo thứ tự đã biết.
Các dạng bài tập thường gặp ở căn bậc hai
Bài tập 1: So sánh:
a) 2 và √3 b) 7 và √51
Giải:
a) Ta có: 2 = √4 mà 4 > 3 nên √4 > √3 tức 2 > √3
b) Ta có: 7 = √49 mà 49 < 51 nên √49 < √51 tức 7 < √51
Bài tập 2: Tìm căn bậc hai của các số sau: 9; 9/25; 1,21; -144.
Lời giải:
– Vì 9 > 0 nên 9 có hai căn bậc hai là 3 và -3, vì 32 = 9 và (-3)2 = 9.
– Vì 9/25 > 0 nên 9/25 có hai căn bậc hai là 3/5 và -3/5, vì (3/5)2 = 9/25 và (-3/5)2 = 9/25.
– Vì 1,21 > 0 nên 1,21 có hai căn bậc hai là 1,1 và -1,1, vì 1,12 = 1,21 và (-1,1)2 = 1,21.
– Theo tính chất, số âm không tồn tại căn bậc hai nên -144 không có căn bậc hai.
Bài tập 3: Giải các phương trình sau:
a) x2 = 5. b) x2 + 2 = 0 c) (x – 2)2 = 7
Lời giải:
– Giải phương trình x2 = 5. Do 5 > 0 nên 5 có hai căn bậc hai là √5 và -√5
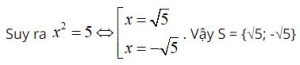
– Giải phương trình x2 = -2. Vì -2 < 0 nên -2 không có căn bậc hai. Suy ra phương trình vô nghiệm. Vậy S = ∅
– Giải phương trình (x – 2)2 = 7. Do 7 > 0 nên 7 có hai căn bậc hai là √7 và -√7.
Suy ra
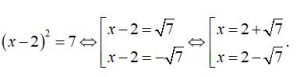
Vậy S = {2 – √7; 2 + √7}
Bài tập 4: Nghiệm của phương trình
![]()
Lời giải:
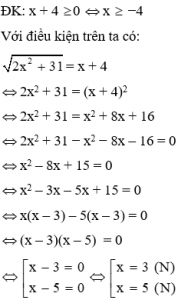
Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình