Số vô tỉ là gì? Khái niệm căn bậc hai và bài tập có lời giải chính xác 100%
Tiếp tục ở chuyên mục Toán Học hôm nay, THPT CHUYÊN LAM SƠN sẽ chia sẻ kiến thức về số vô tỉ là gì? Khái niệm về căn bậc hai, sự khác nhau giữa số hữu tỉ và số vô tỉ kèm theo các dạng bài tập về số vô tỉ có lời giải để các bạn cùng tham khảo nhé
Nội Dung
Số vô tỉ là gì?
Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn. Nói cách khác số vô tỉ là số không phải số hữu tỉ, nghĩa là số không thể biểu diễn được dưới dạng a/b (với a, b là các số nguyên).
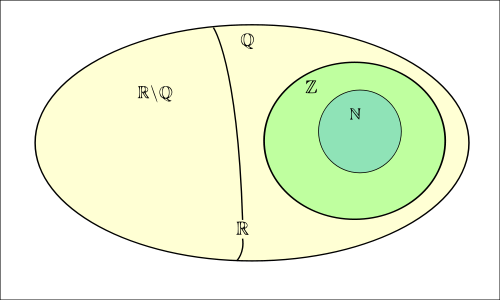
Tập hợp các số vô tỉ được kí hiệu là I.
I ={x|x ≠ m/n,∀m,n∈Z}
Ví dụ: 2,71828…là số vô tỉ
Tính chất số vô tỉ
- Tập hợp số vô tỉ là tập hợp không đếm được.
Ví dụ:
Số vô tỉ: 0,1010010001000010000010000001…(đây là số thập phân vô hạn không tuần hoàn)
Số pi (π): 3,14159 26535 89793 23846 26433 83279 50 288….
Sự khác biệt giữa số hữu tỉ và vô tỉ
Số hữu tỉ và số vô tỉ khác nhau như sau:
- Số hữu tỉ bao gồm số thập phân vô hạn tuần hoàn, còn số vô tỉ là các số thập phân vô hạn không tuần hoàn.
- Số hữu tỉ chỉ là phân số, còn số vô tỉ có rất nhiều loại số
- Số hữu tỉ là số đếm được, còn số vô tỉ là số không đếm được.
Ví dụ: Số hữu tỉ là ¾ còn số vô tỉ là 0,1112323123153436791…
Khái niệm về căn bậc hai
a) Định nghĩa: Căn bậc hai của một số a không âm là số x sao cho x2 = a
- Số dương a có đúng hai căn bậc hai là √a; −√a
- Số 0 chỉ có một căn bậc hai là số 0 : √0 = 0
b) Tính chất: Với hai số dương bất kì a và b
- Nếu a = b thì√a=√b
- Nếu a < b thì √a < √b
Các dạng bài tập về số vô tỉ có lời giải
Dạng 1: Tìm căn bậc hai của một số cho trước
Phương pháp: Sử dụng định nghĩa căn bậc hai
Ví dụ: Số 9 có hai căn bậc hai là 3 và -3 vì 9 = 32 = (−3)2
Ví dụ 2: Tìm căn bậc hai của 16
Lời giải
Ta có : 42 = 16 và (-4)2 = 16
Nên 4 và – 4 là các căn bậc hai của 16
Ví dụ 3: Tìm căn bậc hai của:
a) 25. b) 0,0001. c) 9/25. d) -6.
Hướng dẫn giải
a) Căn bậc hai của 25 là √25 = 5 và -√25 = – 5
b) Căn bậc hai của 0,0001 là √0,0001 = 0,01 và – √0,0001 = – 0,01
c) Căn bậc hai của 9/25 là √9/25 = 3/5 và -√9/25 = -3/5
d) Do -6 nên không tồn tại căn bậc hai của -6.
Dạng 2: Tìm một số khi biết căn bậc hai của nó
Phương pháp: Nếu √x = a (a≥0) thì x = a2
Ví dụ: √x = 5 ⇒ x = 52 ⇒ x = 25
Ví dụ 2: Hãy cho biết mỗi số sau là căn bậc hai của số nào?
2;0; -1; 1/2; √3; -0,4
Hướng dẫn giải
Các số 2;0; -1; 1/2; √3; -0,4 lần lượt là căn bậc hai của các số: 4; 0; 1;1/4 ; 3; 0,16.
Dạng 3: So sánh các căn bậc hai
Phương pháp: Với hai số dương bất kì a và b:
- Nếu a = b thì √a = √b.
- Nếu a < b thì √a < √b
Ví dụ 1. So sánh:
a) √2 với √3
b) 3 với √10.
Hướng dẫn giải
a) Vì 2 < 3 nên √2 < √3
b) Ta có 3 < √9 mà 9< 10 nên √9 < √10. Do đó 3 < √10.
Ví dụ 2. So sánh hai số thực sau:
a) √9.16 với √9.√16.
b) 3 √7 với 8.
c) 2 √3 với 3 √2.
Hướng dẫn giải
a) Ta có √9.16 = √144 = √122 = 12;
√9.√16 = √32.√42 = 3.4 = 12.
Vậy √9.16 = √9.√16.
b) Ta có 3√7 = √9.√7 = √63,8 = √64
Mà 64 > 63 nên √64 > √63.
Vậy 3 √7 < 8.
c) Ta có 2√3 = √4.√3 = √12 và 3√2 = √9.√2 = √18
Mà 18 > 12 nên √18 > √12.
Vậy 2 √3 < 3 √2.
Bên trên chính là toàn bộ lý thuyết về số vô tỉ là gì kèm theo các dạng bài tập có thể giúp các bạn hệ thống lại kiến thức để áp dụng vào làm bài tập nhé