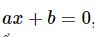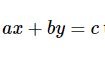[Phương Trình Tiếp Tuyến] Đồ thị, Song song, Tại 1 điểm, Đường cong

Phương trình tiếp tuyến là gì ? Có bao nhiêu dạng phương trình tiếp tuyến ? Mời các bạn đón xem thông tin cụ thể chính xác ở đây.

Phương trình tiếp tuyến của một đồ thị hàm số

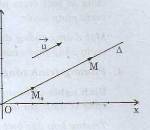
Ý nghĩa hình học của đạo hàm: Đạo hàm của hàm số $y=f\left(x\right)$ tại điểm $x_0$ là hệ số góc của tiếp tuyến với đồ thị $\left(C\right)$ của hàm số tai điểm $M\left(x_0;y_0\right)$ .

Khi đó phương trình tiếp tuyến của $\left(C\right)$ tại điểm $M\left(x_0;y_0\right)$ là $y=y^{\prime }\left(x_0\right)\left(x-x_0\right)+y_0$

Nguyên tắc chung để lập được phương trình tiếp tuyến ta phải tìm được hoành độ tiếp điểm $x_0$

Phương trình tiếp tuyến của một đường tròn

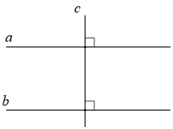
Dạng 1: Tiếp tuyến tại một điểm M₀(x₀, y₀) thuộc đường tròn.

Ta dùng công thức tách đôi tọa độ.

– Nếu phương trình đường tròn là:

x² + y²– 2ax – 2by + c = 0 thì phương trình tiếp tuyến là:  xx₀ + yy₀– a(x + x₀) – b(y + y₀) + c = 0

– Nếu phương trình đường tròn là:

(x – a)² + (y – b)² = R² thì phương trình tiếp tuyến là:

(x – a)(x₀– a) + (y – b)(y₀– b) = R² (h.73)

Dạng 2:Tiếp tuyến vẽ từ một điểm I(x₀, y₀)  cho trước ở ngoài đường tròn.

Viết phương trình của đường  qua I(x₀, y₀):

y – y₀ = m(x – x₀)    mx – y – mx₀ + y₀ = 0        (1)

Cho khoảng cách từ tâm I của đường tròn (C) tới  bằng R, ta tính được m; thay m vào (1) ta được phương trình tiếp tuyến.

* Ghi chú: Ta luôn luôn tìm được hai đường tiếp tuyến. (h. 74)

  Dạng 3: Tiếp tuyến  song song với một phương cho sẵn có hệ số góc k.

Phương trình của  có dạng:

y = kx + m (m chưa biết)    kx – y + m = 0

Cho khoảng cách từ tâm I đến (D) bằng R, ta tìm được m.

Phương trình tiếp tuyến vuông góc với đường thẳng

Các mệnh đề được ứng dụng để viết phương trình tiếp tuyến vuông góc với đường thẳng

Để viết phương trình tiếp tuyến vuông góc với đường thẳng thì các mệnh đề sau sẽ được ứng dụng: – Đường thẳng d có phương trình: y = kx + b ( hệ số góc là k)
– Hệ số góc của tiếp tuyến T của hàm số y = f(x) tại điểm x0 là f'(x0)
– Hai đường thẳng vuông góc với nhau khi nó có tích các hệ số góc là -1
– Phương trình tiếp tuyến T của hàm số y = f(x) tại điểm M0 ( x0;y0) là:
y = f'(x0)(x-x0) + y0

Cách trình bày cụ thể viết phương trình tiếp tuyến vuông góc

Ứng dụng viết phương trình tiếp tuyến biết tiếp tuyến vuông góc với đường thằng y= ã + b để dễ hiểu hơn nhé!

– Xét hàm số y=f(x).

Gọi M (x0;y0) là tiếp điểm, vậy phương trình tiếp tuyến tại M sẽ có dạng: y = f'(x0)(x-x0) + y0 (1)

Suy ra hệ số góc của phương trình tiếp tuyến tại M là k = f'(x0)

– Vì tiếp tuyến tại M vuông góc với đường thằng y = ax + b nên 2 hệ số góc sẽ có tích là -1. Vậy k = f'(x0) = -1/ax

Giải phương trình sẽ tìm được x0 rồi viết phương trình tiếp tuyến.

– Lưu ý: Với dạng bài viết phương trình tiếp tuyến thì điều kiện cần để tiếp tuyến tại A buông góc với tiếp tuyến tại B là: f'(Xa).f'(Xb) = -1 với Xa # Xb