Chia đa thức với đơn thức là gì? Quy tắc chia đa thức với đơn thức và bài tập có lời giải chính xác 100%
Chia đa thức cho đơn thức được thptchuyenlamson.vn sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn toán học hiệu quả hơn. Mời các bạn tham khảo.
Tham khảo thêm:
Hai góc đối đỉnh là gì? Tính chất và bài tập có đáp án cực hay
Lý thuyết hàm số và phương pháp giải bài tập có lời giải từ A – Z
Công thức tính đường kính hình tròn và bài tập có lời giải từ A – Z
Nội Dung
Chia đa thức với đơn thức
Với A là đa thức và B là đơn thức, B≠0. Ta nói A chia hết cho B nếu tìm được một biểu thức Q (Q có thể là đa thức hoặc đơn thức) sao cho A= B.Q.
Kí hiệu: B= A : B hoặc Q= A/B
Trong đó:
- A là đa thức bị chia.
- B là đơn thức chia.
- Q là thương .
Quy tắc chia đa thức với đơn thức
Muốn chia đa thức A cho đơn thức B (trường hợp các hạng tử của đa thức A đều chia hết cho đơn thức B), ta chia mỗi hạng tử của A cho B rồi cộng các kết quả với nhau.
Chú ý: Trường hợp đa thức A có thể phân tích thành nhân tử, thường ta phân tích trước để rút gọn cho nhanh.
Một số dạng toán về chia đa thức cho đơn thức cơ bản
Dạng 1: Thực hiện phép tính và rút gọn biểu thức
Phương pháp: Sử dụng quy tắc chia đa thức cho đơn thức để thực hiện phép tính và rút gọn biểu thức.
Ví dụ 1: Thực hiện phép tính
a, Ta có: (−12x4y + 4x3 − 8x2y2) : (−4x2)
= (−12x4y) : (−4x2) + (4x3) : (−4x2) − (8x2y2) : (−4x2)
= 3x2y − x + 2y2
b, Ta có: (- 2x5 + 6x2 – 4x3):2x2 = (- 2x5:2x2) + (6x2:2x2) – (4x3:2x2)
= – x5 – 2 + 3x2 – 2 – 2x3 – 2 = – x3 – 2x + 3.
c, Ta có: (12x4y3 + 8x3y2 – 4xy2):2xy = (12x4y3:2xy) + (8x3y2:2xy) – (4xy2:2xy)
= 6x4 – 1.y3 – 1 + 4x3 – 1.y2 – 1 – 2x1 – 1.y2 – 1 = 6x3y2 + 4x2y – 2y
Ví dụ 2: Thực hiện phép tính
a, Ta có: (1/2a2x4 + 4/3ax3 – 2/3ax2):(- 2/3ax2)
= (1/2a2x4: – 2/3ax2) + (4/3ax3: – 2/3ax2) + (- 2/3ax2: – 2/3ax2)
= – 3/4ax2 – 2x + 1
b) Ta có 4(3/4x – 1) + (12x2 – 3x):(- 3x ) – (2x + 1)
= 4(3/4x – 1) + [(12x2: – 3x) + (- 3x: – 3x)] – (2x + 1)
= 4(3/4x – 1) + (- 4x + 1) – (2x + 1) = 3x – 4 + 1 – 4x – 2x – 1 = – 3x – 4
Ví dụ 3: Thực hiện phép tính
a) Ta có: (2xy3 + 4x2y2) : xy
= (2xy3 : xy) + (4x2y2 : xy)
= 2y2 + 4xy
b) Ta có: (5x4y3 – x3y2 + 2x2y) : (-x2y)
= [5x4y3 : (-x2y)] – [x3y2 : (-x2y)] + [2x2y : (-x2y)]
= -5x2y + xy – 2
c) Ta có: [(xy)3 – 3(xy)2z + 2(xy)3] : (yzx)2
= [(xy)3 : (yzx)2] – [3(xy)2z : (yzx)2] + [2(xy)3 : (yzx)2]
= xy – 3z + 2(xy)3
d) Ta có: [4(x – y)5 + 2(x – y)3 – 3(x – y)2 ]: (y – x)2
= [4(x – y)5 + 2(x – y)3 – 3(x – y)2 ]: (x – y)2
= [4(x – y)5 : (x – y)2] + [2(x – y)3: (x – y)2] – [3(x – y)2 : (x – y)2]
= 4(x – y)3 + 2(x – y) – 3
Dạng 2: Tính giá trị của biểu thức tại x = x0
Phương pháp: Thay x = x0 vào biểu thức rồi thực hiện phép tínhNếu biểu thức có nhiều biến thì ta thay lần lượt từng biến theo giả thiết.
Ví dụ 1: Tính giá trị biểu thức
a, Ta có: A = (x2y + y2x) : xy
= x2y : xy + y2x : xy
= x + y
Với x = 1; y = 1 ta có: A = x + y = 1 + 1 = 2
b) Ta có: B = [(2x2y)2 + 3x4y3 – 6x3y2] : (xy)2
B = [(2x2y)2 : (xy)2] + [3x4y3: (xy)2] – [6x3y2: (xy)2]
B = 4x2 + 3x2y – 6x
Thay x = y = -2 vào biểu thức ta được B = 4
c) Ta có: C = (-2x2y2 + 4xy – 6xy3) : (2/3 xy)
C = [-2x2y2 : (2/3 xy)] + [4xy : (2/3 xy)] – [6xy3 : (2/3 xy)]
C = -3xy +6 – 9y2
Thay x = ½ và y = 4 vào biểu thức ta được C = -144
d, Ta có: D = [(15x5y3 – 10x3y2 + 20x4y4)] : (5x2y2)
D = (15x5y3 : 5x2y2) – (10x3y2 : 5x2y2) + (20x4y4 : 5x2y2)
D = 3x3 – 2x + 4x2y2
Thay x = -1; y = 2 vào biểu thức ta được A = 12
Dạng 3: Tìm m để phép tính chia cho trước là phép chia hết
Phương pháp: Đa thức A chia hết cho đơn thức B nếu các hạng tử của đa thức A đều chia hết cho đơn thức B. Đơn thức A chia hết cho đơn thức B khi mỗi biến của B đều là biến của A với số mũ nhỏ hơn hoặc bằng số bằng số mũ của nó trong A
Ví dụ: Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B:
a, A = 7xn−1y5 − 5x3y4
B = 5x2yn
Ta có: A : B = (7xn−1y5 − 5x3y4) : (5x2yn) = (7xn−1y5) : (5x2y4)− (5x3y4) : (5x2yn)
Đa thức A chia hết cho đơn thức B khi
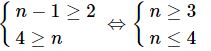
⇒ 3 ≤ n ≤ 4 n ∈ N n ∈ {3; 4}
b, A = -13x17y2n-3 + 22x16y7 và B = -7x3n + 1y6
Ta có: A : B = (-13x17y2n-3 + 22x16y7) : ( -7x3n + 1y6 )
Đa thức A chia hết cho đơn thức B khi
=> 2n – 3 ≥ 6 và 16 ≥ 3n + 1
=> n = 5
c, A = 20x8y2n – 10x4y3n + 15x5y6 và B = 3.x2nyn + 1
Ta có: A : B = ( 20x8y2n – 10x4y3n + 15x5y6 ) : ( 3.x2nyn + 1 )
Đa thức A chia hết cho đơn thức B khi
=> 4 ≥ 2n; 2n ≥ n + 1 và 6 ≥ n + 1
=> n = 1
Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình