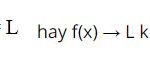Nhân đa thức với đa thức là gì? Quy tắc nhân đa thức với đa thức và bài tập có lời giải chính xác 100%

Bên cạnh nhân đơn thức với đa thức thì dạng toán nhân đa thức với đa thức cũng là một chuyên đề quan trọng. Vậy nhân đa thức với đa thức có quy tắc thế nào? Và có những dạng bài tập nào cần lưu ý về phần kiến thức này? Hãy cùng thptchuyenlamson.vn tìm hiểu câu trả lời qua bài viết về chuyên đề nhân nhiều đa thức với nhau dưới đây!

Tham khảo thêm:

Nội Dung

Quy tắc nhân đa thức với đa thức

Muốn nhân một đa thức với một đa thức ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.

Công thức tổng quát: Cho A, B, C, D là các đa thức

Ta có: (A + B).(C + D)

= A.(C + D) + B.(C + D)

= AC+ AD+ BC+ BD

Các dạng toán nhân đa thức với đa thức cơ bản

Dạng 1: Thực hiện phép tính (hoặc rút gọn biểu thức)

Phương pháp: Sử dụng quy tắc nhân đa thức với đa thức

Ví dụ 1: Tính (x – 5). (2x+ 1)

Ta có: (x- 5). (2x +1)

= x. (2x+ 1) – 5. (2x+ 1)

= x .2x + x.1 – 5.2x – 5.1

= 2x² + x – 10x – 5

= 2x² + (x- 10x) – 5

= 2x² – 9x – 5

Ví dụ 2: Tình (x – xy). (x² + y)

Ta có: (x- xy). (x² + y)

= x.(x² + y) – xy. (x² + y)

= x.x² + xy – xy . x² – xy. y

= x³ + xy – x³y – xy²

Dạng 2: Tính giá trị biểu thức

Phương pháp: Giá trị của biểu thức f(x) tại x⁰ là f(x⁰)

TÍnh giá trị biểu thức: A= (x- 1)(x² + 1) – (2x + 3)(x² -2 ) với x= 2

Ta có: A = (x − 1) (x² + 1) − (2x + 3) (x² − 2)

⇔ A = x. x² + x.1 − 1.x² − 1.1 − 2x. x² + 2x.² − 3.x² + 3.2

⇔ A = x³ + x − x² − 1 − 2x³ + 4x − 3x² + 6

⇔ A = −x³ − 4x² + 5x + 5

Tại x = 2 ⇒ A = −23 − 4.22 + 5.2 + 5 = −9

Dạng 3: Tìm x

Phương pháp: Sử dụng các quy tắc nhân đa thức với đa thức để biến đổi đưa về dạng tìm x cơ bản

Ví dụ: Tìm x biết: (x + 2)(x + 3) − (x − 2)(x + 5) = 6

Ta có: (x + 2)(x + 3) − (x − 2)(x + 5) = 6

⇔ x. x + 3.x + 2.x + 2.3 − x. x − 5.x + 2.x + 2.5 = 6

⇔ x² + 3x + 2x + 6 − x² − 5x + 2x + 10 = 6

⇔ 2x + 16 = 6

⇔ 2x = −10

⇔ x = −5

Dạng 4: Chứng minh biểu thức có giá trị

Phương pháp: ta cũng sẽ áp dụng quy tắc nhân đa thức với đa thức để rút gọn biểu thức đến khi không còn biến số.

Ví dụ: chứng minh biểu thức sau có giá trị không phụ thuộc vào giá trị của biến số x:

(3x – 5)(2x + 11) – (2x + 3)(3x + 7)

Ta có: (3x – 5)(2x + 11) – (2x + 3)(3x + 7)

=6x²+ 33x – 10x − 55 – (6x²+ 14x + 9x + 14)

= – 55 – 14 = -69

Suy ra: biểu thức không phụ thuộc vào giá trị biến số x.

Dạng 5: Nhân đa thức với đa thức nâng cao

Đây là phần bài tập đa dạng và không có cách làm cụ thể. Bài toán yêu cầu chúng ta phải có sự vận dụng và tổng hợp nhiều kiến thức khác nhau.

Ví dụ: chứng minh rằng với mọi số nguyên n thì: (n²–3n+1)(n+2)–n³+2 chia hết cho 5.

Biến đổi biểu thức ta có: (n²–3n+1)(n+2)–(n³+2)=n³+3n²+n+2n²–6n+2–n³–2=5n²–5n

Suy ra biểu thức chia hết cho 5.

Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình