Cách tính Delta là gì? Công thức và các dạng bài tập chi tiết từ A -Z

Cách tính delta và cách tính delta phẩy trong phương trình bậc hai do đội ngũ giáo viên của chúng tôi biên soạn và giới thiệu cho các bạn học sinh và thầy cô nghiên cứu, học tập tốt môn Toán 9 cũng như luyện tập nhằm chuẩn bị tốt nhất cho kì thi học kì và kì thi vào lớp 10 sắp diễn ra. Mời các bạn tham khảo.

Tham khảo thêm:

• Số thực là gì? Tính chất của số thực và bài tập chi tiết từ A – Z
• Hỗn số là gì? Cách chuyển đổi của hỗn số và bài tập chính xác 100%
• Số hữu tỉ là gì? Cách so sánh số hữu tỉ và bài tập có lời giải từ A – Z

Delta là gì?

Delta là một chữ cái trong bảng chữ Hy Lạp, được kí hiệu là Δ (đối với chữ hoa) và δ (đối với chữ thường). Trong toán học, đặc biệt là Toán 9, ký hiệu Δ chỉ một biệt thức trong phương trình bậc hai mà dựa vào từng giá trị của delta ta có thể kết luận được số nghiệm của phương trình bậc hai.

Ngoài ra delta còn dùng để kí hiệu cho đường thẳng mà các bạn sẽ được học ở các lớp cao hơn.

Phương trình bậc hai một ẩn

Phương trình bậc hai một ẩn (ẩn x) là phương trình có dạng: ax² + bx + c = 0

Trong đó a ≠ 0, a,b là các hệ số, c là hằng số.

Công thức nghiệm của phương trình bậc hai một ẩn

Ta sử dụng một trong hai công thức nghiệm sau để giải phương trình bậc hai một ẩn:

Tính: ∆ = b² – 4ac

+) Nếu ∆ > 0 thì phương trình ax² + bx + c = 0 có hai nghiệm phân biệt:

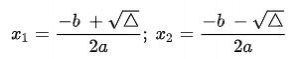
+) Nếu ∆ = 0 thì phương trình ax² + bx + c = 0 có nghiệm kép:

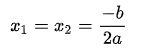
+) Nếu ∆ < 0 thì phương trình ax² + bx + c = 0  vô nghiệm:

 Tính : ∆’ = b’² – ac trong đó b’ = b/2 ( được gọi là công thức nghiệm thu gọn)

+) Nếu ∆’ > 0 thì phương trình ax² + bx + c = 0 có hai nghiệm phân biệt:

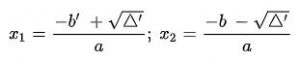
+)Nếu ∆’ = 0 thì phương trình ax² + bx + c = 0 có nghiệm kép:

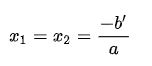
+) Nếu ∆’ < 0 thì phương trình ax² + bx + c = 0 vô nghiệm.

Hê thức Viet là gì?

Cho phương trình bậc 2 một ẩn: ax² + bx + c = 0 (a ≠ 0). có 2 nghiệm x₁ và x₂. Khi đó 2 nghiệm này thỏa mãn hệ thức sau: thì ta có Công thức Vi-et như sau:

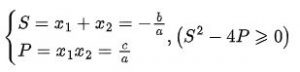
Các dạng toán thường gặp ở Delta

Bài 1: Giải các phương trình dưới đây:

a, x² – 5x + 4 = 0

b, 6x² + x + 5 = 0

c, 16x² – 40x + 25 = 0

d, x² – 10x + 21 = 0

e, x² – 2x – 8 = 0

f, 4x² – 5x + 1 = 0

g, x² + 3x + 16 = 0

Lời giải:

a, x² – 5x + 4 = 0

Ta có: ∆ = b² – 4ac = (-5)² – 4.1.4 = 25 – 16 = 9 > 0

Phương trình đã cho có hai nghiệm phân biệt:

Vậy tập nghiệm của phương trình là: S = {1; 4}

b, 6x² + x + 5 = 0

Ta có:  ∆ = b² – 4ac = 1² – 4.6.5 = 1 – 120 = – 119 < 0

Phương trình đã cho vô nghiệm.

Vậy phương trình vô nghiệm.

c, 16x² – 40x + 25 = 0

Ta có: ∆’ = b’² – ac = (-20)² – 16.25 = 400 – 400 = 0

Phương trình đã cho có nghiệm kép: x₁ = x₂ = -b/a = 20/16 = 5/4

Vậy tập nghiệm của phương trình là: S ={5/4}

d, x² – 10x + 21 = 0

Ta có: ∆’ = b’² – ac = (-5)² – 1.21 = 25 – 21 = 4 > 0

Phương trình đã cho có hai nghiệm phân biệt:

Vậy phương trình có tập nghiệm S = {-7; -3}

e, x² – 2x – 8 = 0

Ta có: ∆’ = b’² – ac = (-1)² – 1.(-8) = 1 + 8 = 9 > 0

Phương trình đã cho có hai nghiệm phân biệt:

Vậy tập nghiệm của phương trình là S = {-2; 4}

f, 4x² – 5x + 1 = 0

Ta có:  ∆ = b² – 4ac = (-5)² – 4.4.1 = 25 – 16 = 9 > 0

Phương trình đã cho có hai nghiệm phân biệt: x₁= 1; x₂ =1/4

Vậy tập nghiệm của phương trình là: S ={1; 1/4}

g,  x² + 3x + 16 = 0

Ta có: ∆ = b² – 4ac = 3² – 4.1.16 = 9 – 64 = -55 < 0

Vậy phương trình vô nghiệm.

Bài 2: Cho phương trình x² – 6x + m² – 4m = 0 (1)

a, Tìm m để phương trình có nghiệm x = 1

b, Tìm m để phương trình có nghiệm kép

Lời giải:

a, x = 1 là nghiệm của phương trình (1). Suy ra thay x = 1 vào phương trình (1) có:

Xét phương trình (2)

Phương trình (2) có hai nghiệm phân biệt m₁= 5 và m₂= -1

Vậy với m = 5 hoặc m = -1 thì x = 1 là nghiệm của phương trình (1)

b, Xét  phương trình (1) có:

Để phương trình (1) có nghiệm kép khi và chỉ khi Δ’ =0

m² + 4m + 9 = 0 (2)

Bài 3: Tìm m để phương trình x² – 2(m – 2)x – 6m = 0 có nghiệm x₁; x₂ sao cho biểu thức x₁² + x₂² đạt giá trị nhỏ nhất.

Giải:

Bài 4: Tìm m để mx² – 2(m + 1)x + m + 3 = 0 là phương trình bậc hai nhận x = -2 là nghiệm.

Giải:

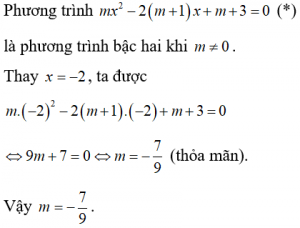
Bài 5: Tìm m để hai phương trình x² + x + m – 2 = 0 (1) và x² + (m – 2)x + 1 = 0 (2) có nghiệm chung.

Giải:

Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình