Phương trình đường tròn và các dạng bài tập lớp 10, 12

Khi học đến phương trình đường tròn bạn gặp khó khăn hãy xem ngay những thông tin mà THPT Chuyên Lam Sơn của chúng tôi cung cấp bên dưới đây để có thể hiểu rõ kiến thức hơn.

1. Phương trình đường tròn 

Phương trình đường tròn tâm I(a; b), bán kính R là:

(x – a)² – (y – b)² = R²

Nếu a² + b² – c  > 0 thì phương trình x² + y² – 2ax – 2by + c = 0 là phương trình của đường tròn tâm I(a;b), bán kính:

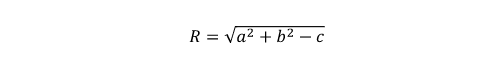
=> Nếu a² + b² – c  = 0 thì chỉ có 1 điểm M(x; y) thoả mãn phương trình x² + y² – 2ax – 2by + c = 0

=> Nếu a² + b² – c  < 0 thì không có điểm M(x; y) nào thoả mãn phương trình x² + y² – 2ax – 2by + c = 0

Nhận xét

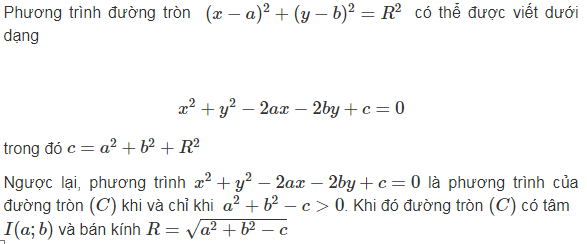
2. Phương trình tiếp tuyến của đường tròn

3. Các dạng bài tấp về pt đường tròn

Ví dụ 1:

Đề bài

1. Cho hai điểm A(3; -4) và B(-3; 4).
2. Viết phương trình đường tròn (C) nhận AB là đường kính.

Lời giải :

Gọi I là đường tròn nhận AB là đường kính

⇒ I là trung điểm của AB ⇒ I (0; 0)

$\begin{array}{cc}& AB=\sqrt{{(-3-3)}^2+{(4+4)}^2}=10\\ & \Rightarrow R=\frac{AB}{2}=5\end{array}$

Phương trình đường tròn (C) nhận AB là đường kính là: x² + y² = 25

Ví dụ 2:

Đề bàiHãy cho biết phương trình nào trong các phương trình sau đây là phương trình đường tròn:

1. 2x² + y² – 8x + 2y – 1 = 0;
2. x² + y² + 2x – 4y – 4 = 0;
3. x² + y² – 2x – 6y + 20 = 0;
4. x² + y² + 6x + 2y + 10 = 0.

Lời giải chi tiết

2x² + y² – 8x + 2y – 1 = 0;

Phương trình trên không là phương trình đường tròn vì hệ số của $x^2$ và $y^2$ khác nhau.

x² + y² + 2x – 4y – 4 = 0;

a = -1; b = 2; c = -4 ⇒ a² + b² – c = 9 > 0

⇒ Phương trình trên là phương trình đường tròn.

x² + y² – 2x – 6y + 20 = 0;

a = 1; b = 3; c = 20 ⇒ a² + b² – c = -10 < 0

⇒ Phương trình trên không là phương trình đường tròn.

x² + y² + 6x + 2y + 10 = 0.

a = -3; b = -1; c = 10 ⇒ a² + b² – c = 0

⇒ Phương trình trên không là phương trình đường tròn.