Lý thuyết và cách tính hàm số liên tục kèm theo VD có lời giải chi tiết nhất

Hàm số liên tục là một phần kiến thức quan trọng trong Toán Học. Để làm được các bài tập về dạng này bạn cần nắm chắc lý thuyết và các tính chất cơ bản. Dưới đây thptchuyenlamson.vn xin tổng hợp toàn bộ kiến thức và các dạng bài tập giúp bạn học tốt hơn. Hãy cùng theo dõi bài viết này nhé!

Tham khảo thêm:

• Công Thức Đạo Hàm Log, căn bậc 3 , căn u, căn x, căn logarit
• Công thức tính Chu Vi Hình Chữ Nhật và bài tập có lời giải từ A – Z
• Công thức tính diện tích tam giác vuông, cân, đều chính xác

Hàm số liên tục là gì?

Hàm số y = f(x) gọi là hàm số liên tục trên khoảng nếu số đó liên tục mọi điểm thuộc khoảng đó. Cụ thể hơn, ta ó định nghĩa khái quát chung như sau:

Đồ thị hàm số liên tục có dạng:

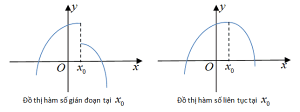
Hàm số liên tục tại một điểm

 

Cho hàm số y = f(x) xác định trên khoảng K và x0 ∈ K.

Hàm số y = f(x) được gọi là liên tục tại x0 nếu :

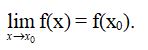
Hàm số liên tục trên một khoảng

Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.

Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và

Nhận xét: Đồ thị của hàm số liên tục trên một khoảng là một đường liền trên khoảng đó.

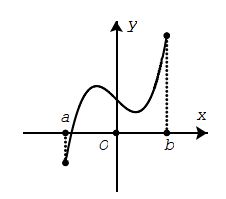
Hàm số liên tục trên khoảng (a;b)

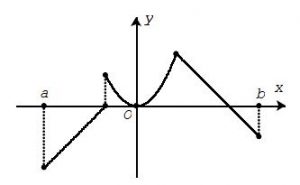
Một số định lý của hàm số liên tục

Định lí 1:

• Hàm số đa thức liên tục trên toàn bộ tập số thực R.
• Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng.

Định lí 2: Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x0. Khi đó:

• Các hàm số y = f(x) + g(x), y = f(x) – g(x) và y = f(x).g(x) liên tục tại x0
• Hàm số f(x)/g(x) liên tục tại x0 nếu g(x0) ≠ 0.

Định lí 3: Nếu hàm số y = f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0, thì tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = 0..

Định lí 3 thường được áp dụng để chứng minh sự tồ tại nghiệm của phương trình trên một khoảng và nó còn được phát triển dưới dạng khác như sau:

Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) < 0, thì phương trình f(x) = 0 có ít nhất một nghiệm nằm trong khoảng (a, b).

Các dạng bài tập thường gặp ở hàm số liên tục

Dạng 1: Xét tính liên tục của hàm số tại một điểm cụ thể.

Để xét được tính liên tục của một hàm số đã cho trước tại điểm x0 ta thực hiện lần lượt các bước:

• Bước 1: Kiểm tra xem hàm số đã cho có xác định trên một khoảng chứa x0 hay không sau đó hãy tính giá trị
• tại f(x0).
• Bước 2: Tính limx→x₀f(x). Trong nhiều trường hợp ta cần tính limx→x0 + f(x), limx→x0 – f(x).
• Bước 3: So sánh limx→x0f(x) với f(x0) và kết luận.

Bài 1: Ý kiến sau đúng hay sai?

“Nếu hàm số y = f(x) liên tục tại điểm x₀ và hàm số y = g(x) không liên tục tại x₀, thì y = f(x) + g(x) là một hàm số không liên tục tại x0″.

Lời giải:

Ý kiến trên đúng.

Vì giả sử ngược lại hàm số y = h(x) = f(x) + g(x) là hàm số liên tục tại x₀. Khi đó, hàm số g(x) = h(x) – f(x) là hiệu của hai hàm số liên tục tại x₀ nên hàm số g(x) là hàm số liên tục x₀ ( định lí về hàm số liên tục)

=> Mâu thuẫn với giả thiết là hàm số g(x) không liên tục tại x_0.

Bài 2: Chứng minh rằng:

Lời giải:

a) Hàm số f(x) = x³ – x + 3 xác định trên R. Với mọi x_o ∈ R, ta có:

Vậy f liên tục tại điểm x_o.

Do đó hàm số f liên tục tại mọi điểm của R

+) Xét hàm số y = g(x)

Ta có: x² + 1 > 0 với mọi x nên hàm số y= g(x) xác định với mọi x.

Với ∀ x₀ ∈ R ta có:

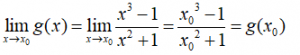
Do đó, hàm số y = g(x) liên tục tại mọi điểm x ∈ R .

b) Với mọi x ≠ 2, ta có:

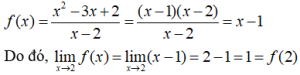
Vậy hàm số f liên tục tại điểm x = 2

c) Với mọi x ≠ 1, ta có:

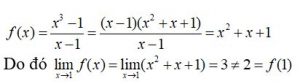
Vậy hàm số f gián đoạn tại điểm x = 1.

Dạng 2: Xét tính liên tục, chứng minh hàm số liên tục trên một khoảng đoạn hoặc tập xác định

Để giải được dạng toán này chúng ta hãy cùng nhau xét ví dụ sau đây nhé:

Rõ ràng ta có thể thấy khi x khác 0 thì hàm số đã cho là luôn là hàm phân thức. Và nó hoàn toàn xác định nên nó liên tục trên từng khoảng.

Do đó, lúc này chúng ta chỉ cần xét tính liên tục tại x = 0. Chúng ta có:

Giá trị của hàm số tại x = 0 là f(0) = 5

Giới hạn của hàm số tại x = 0 là limx→0f(x) = limx→0.2 + 5.x = limx→0(x + 5) = 5

Ta thấy limx→0f(x) = f(0) vì vậy mà hàm số đã cho sẽ liên tục tại x = 0

Mẹo nhỏ bạn có thể sử dụng chức năng của máy tính để tính hàm số liên tục bấm máy. Hãy sử dụng phím Solve trên máy để kiểm tra nhanh đáp án của bài toán nhé.

Bài 1; Chứng minh rằng:

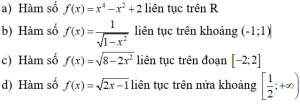
Giải:

a) Hàm số f(x) = x⁴ – x² + 2 xác định trên R. Với mọi x_o ∈ R ta có:

Vậy f liên tục tại x_onên f liên tục tại R

b) Hàm số f xác định khi và chỉ khi:

1 – x² > 0 ⇔ – 1 < x < 1

Vậy hàm số f xác định trên khoảng (-1;1)

Với mọi x_o ∈ (-1;1), ta có:

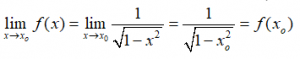
Vậy hàm số f liên tục tại điểm x_o. Do đó f liên tục trên khoảng (-1;1)

Bài 2: Chứng minh rằng mỗi hàm số sau đây liên tục trên tập xác định của nó:

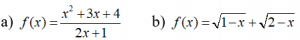
Giải:

a) Tập xác định của hàm số f là R\{-1/2}

Hàm phân thức hữu tỉ f liên tục trên tập xác định của nó, tức là liên tục trên các khoảng

(-∞; 1/2) và (-1/2; +∞).

b) Hàm số f xác định khi và chỉ khi:

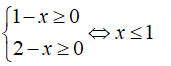
Do đó tập xác định của hàm số f là (-∞; 1]

Với mọi x ∈ (-∞; 1) ta có:

Dạng 3: Tìm điều kiện để hàm số liên tục tại một điểm

Để giải được dạng toán này ta sử dụng phương pháp sau. Đầu tiên cần vận dụng điều kiện phương trình có nghiệm và hàm số liên tục:

Điều kiện để hàm số liên tục tại x0:

Điều kiện để hàm số đã cho liên tục trên một tập D là f(x) đó là liên tục tại mọi điểm thuộc D.

Phương trình f(x) = 0 phải có ít nhất một nghiệm nếu hàm số y = f(x) liên tục trên D, 2 số a và b đều thuộc D.

Bài 1: Giả sử hàm số y = f(x) liên tục trên đoạn [a; b] với f(a) và f(b) trái dấu nhau.

Hỏi đồ thị của hàm số có cắt trục hoành tại điểm thuộc khoảng (a; b) không?

+ Bạn Hưng trả lời rằng: “Đồ thị của hàm số y = f(x) phải cắt trục hoành Ox tại một điểm duy nhất nằm trong khoảng (a; b)”.

+ Bạn Lan khẳng định: “Đồ thị của hàm số y = f(x) phải cắt trục hoành Ox ít nhất tại một điểm nằm khoảng (a; b)”.

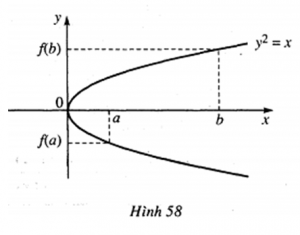
+ Bạn Tuấn thì cho rằng: “Đồ thị của hàm số y = f(x) có thể không cắt trục hoành trong khoảng (a; b), chẳng hạn như đường parabol ở hình (h.58).

Câu trả lời của bạn nào đúng, vì sao?

Lời giải:

– Bạn Lan nói đúng vì f(a) và f(b) trái dấu nên tồn tại ít nhất 1 giá trị x sao cho f(x) = 0, do đó đồ thị hàm số y = f(x) cắt trục hoành tại ít nhất 1 điểm

– Bạn Hưng sai vì có thể có 2 giá trị x sao cho f(x) = 0

– Đường parabol trên hình 58 là đồ thị hàm số y2 = x ⇒ đồ thị hàm số y = f(x) sẽ là 1 nửa nằm trên hoặc 1 nửa nằm dưới trục hoành

Khi đó f(a) và f(b) cùng dấu, mâu thuẫn với điều kiện f(a) và f(b) trái dấu

⇒ Ví dụ của Tuấn sai

Bài 2: Cho hàm số

Giải:

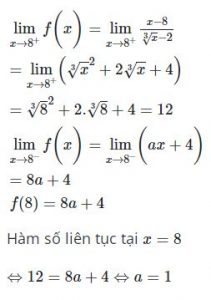
Dạng 4: Tìm điều kiện để hàm số liên tục trên một khoảng đoạn hoặc tập xác định

Để giải được dạng này bạn cần áp dụng các định lý 1 và 2 sao cho tìm được tính liên tục của nó trên từng khoảng xác định. Nếu hàm số đã cho được xác định bởi 2 hoặc 3 công thức thì ta sẽ xét tính liên tục tại các điểm đặc biệt đó.

Ví dụ 1: Tìm a để hàm số liên tục trên tập xác định: f(x) = (2 – 7x + 5×2)/(x – 1) với điều kiện x khác 1 hoặc x = 1

Hướng dẫn cách giải:

Đầu tiên xét trường hợp x khác 1 thì hàm số đã cho là phân thức hữu tỉ.

Khi x = 1 thay vào hàm số đã cho. Khi đó hàm số f(x) liên tục tại điểm x = 1 khi và chỉ khi m = -4/3.

Ví dụ 2: Hãy tìm hai số a và b thỏa mãn 1 < a < b < 2, sao cho phương trình trong Ví dụ 3 ở trên có ít nhất một nghiệm thuộc khoảng (a; b).

Ta có:

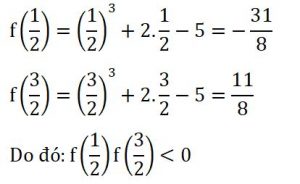
y = f(x) là hàm số đa thức liên tục trên R.

Do đó f(x) liên tục trên ( 1/2; 3/2 )

Từ đó suy ra, phương trình f(x) = 0 có ít nhất một nghiệm x_o ∈ (0;2)

Dạng 5: Ứng dụng hàm số liên tục chứng minh phương trình có nghiệm

Đầu tiên ta cần áp dụng định lý: Nếu hàm số y = f(x) liên tục trên đoạn [a; b] cho trước và f(a).f(b) nhỏ hơn 0, thì phương trình f(x) = 0 sẽ luôn có ít nhất 1 nghiệm nằm trong khoảng (a; b).

Các bước cụ thể để làm bài chứng minh phương trình có nghiệm như sau:

• Bước 1: Biến đổi phương trình đã cho cần chứng minh về dạng f(x) = 0.
• Bước 2: Tiếp theo cần tìm 2 số a và b (a nhỏ hơn b) sao cho f(a).f(b) nhỏ hơn 0
• Bước 3: Cuối cùng chứng minh hàm số y = f(x) luôn liên tục trên đoạn [a; b] đã cho.

Bài 1: Chứng minh rằng phương trình:

a. 2×3 – 6x + 1 = 0 có ít nhất hai nghiệm.

b. cos x = x có nghiệm

Lời giải:

a. Đặt f(x) = 2×3 – 6x + 1

TXĐ: D = R

f(x) là hàm đa thức nên liên tục trên R.

Ta có: f(-2) = 2.(-2)3 – 6(-2) + 1 = – 3 < 0

f(0) = 1 > 0

f(1) = 2.13 – 6.1 + 1 = -3 < 0.

⇒ f(-2).f(0) < 0 và f(0).f(1) < 0

⇒ f(x) = 0 có ít nhất một nghiệm thuộc khoảng (-2; 0) và ít nhất một nghiệm thuộc (0 ; 1)

⇒ phương trình f(x) = 0 có ít nhất hai nghiệm.

b. Xét hàm số g(x) = x – cos x liên tục trên R.

do đó liên tục trên đoạn [-π; π] ta có:

g(-π) = -π – cos (-π) = -π + 1 < 0

g(π) = π – cos π = π – (-1) = π + 1 > 0

⇒ g(-π). g(π) < 0

⇒ phương trình x – cos x = 0 có nghiệm trong (-π; π) tức là cos x = x có nghiệm.

Bài 2: Cho hàm số f(x) = x3 – 1000×2 + 0,01 . phương trình f(x) = 0 có nghiệm thuộc khoảng nào trong các khoảng sau đây ?

Giải:

Ta có hàm số y = f(x) = x³ – 1000x² + 0,01 là hàm liên tục trên R

f(0) = 0.01 và f(-1) = – 1001 + 0.01 < 0. Nên f(0).(-1) < 0.

Vậy hàm số có nghiệm trong khoảng I

Bài 3 : Chứng minh rằng phương trình sau có ít nhất một nghiệm : x7 + 3×5 – 1 = 0

Giải:

Ta có hàm số f(x) = x⁷ + 3x⁵ – 1 liên tục trên R và f(0).f(1) = – 3 < 0

Suy ra phương trinh f(x) = 0 có ít nhất một nghiệm thuộc (0,1).