Số thực là gì? Tính chất của số thực và bài tập chi tiết từ A – Z

Trong bài viết dưới đây, THPT CHUYÊN LAM SƠN sẽ giới thiệu tới các bạn lý thuyết số thực là gì? Tính chất của số thực và các dạng bài tập về số thực có lời giải chi tiết để các bạn hệ thống lại kiến thức để áp dụng vào làm bài tập nhé

Nội Dung

Số thực là gì?

Số thực là một giá trị của một đại lượng liên tục có thể biểu thị một khoảng cách dọc theo một đường thẳng. Hay nói cách khác số thực là tập hợp các số hữu tỉ và vô tỉ. Ký hiệu là R.

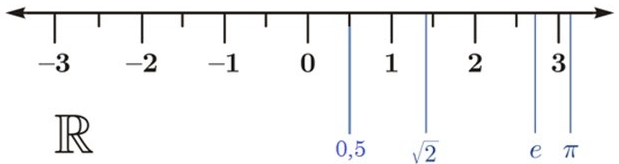
Ví dụ: số nguyên -5, phân số 4/3 và tất cả cả các số vô tỉ như: √2(1.41421356…, căn bậc 2 của số 2, số đại số vô tỉ)

Tính chất của số thực

Bất kỳ số thực khác không là số âm hoặc số dương.
Tổng và tích của hai số thực không âm cũng là một số thực không âm, nghĩa là chúng được đóng trong các phép toán này và tạo thành một vành số dương, từ đó tạo ra một thứ tự tuyến tính của các số thực dọc theo một trục số.
Những số thực sẽ tạo nên một tập hợp vô hạn các số mà không thể đơn ánh tới tập hợp vô hạn của các số tự nhiên. Điều này chứng tỏ có nhiều số thực hơn so với các phần tử trong bất kỳ tập hợp đếm được nào khác.
Có một hệ thống các tập hợp con vô hạn có thể đếm được của các số thực. Các phần bù của tất cả các tập hợp này (số thực vô tỷ, số siêu việt và số không tính toán được) đối với các số thực, đều là các tập hợp vô hạn không đếm được.
Số thực có thể được sử dụng để thể hiện các phép đo đại lượng liên tục. Chúng có thể được biểu thị bằng các biểu diễn thập phân, hầu hết chúng có một chuỗi các chữ số vô hạn ở bên phải dấu thập phân; chúng thường được biểu diễn như 324.823122147…, trong đó dấu chấm lửng (ba dấu chấm) chỉ ra rằng vẫn còn nhiều chữ số nữa sẽ xuất hiện.

Các dạng bài tập về số thực thường gặp có lời giải

Tham khảo thêm:

Dạng 1. Bài tập về định nghĩa các tập hợp số

Phương pháp giải: Trước tiên, bạn cần nắm vững các kí hiệu tập hợp số:

N : Tập hợp các số tự nhiên
Q : tập hợp các số hữu tỉ
R : tập hợp các số thực
Z : tập hợp các số nguyên
I : tập hợp các số vô tỉ

Nắm vững quan hệ của các tập hợp số nói trên: N ⊂ Z ⊂ Q ⊂ R ; I ⊂ R.

Ví dụ 1: Điền dấu ∈, ∉, ⊂ thích hợp vào chỗ trống (…):

3 …. Q ; 3 …. R ; 3… I ; -2,53… Q ;

0,2(35) …. I ; N …. Z ; I …. R.

Giải:

a) 3 ∈ Q ; 3 ∈ R ; 3 ∉ I ; -2,53∈ Q ;

b) 0,2(35) ∉ I ; N ∈ Z ; I ⊂ R.

Ví dụ 2: Ta có R ∩ I =

A. R

B. Q

C. ∅

D. I

Lời giải

Do R = I ∪ Q do đó R ∩ I = I

Chọn đáp án D

Dạng 2: So sánh các số thực

Phương pháp giải:

Với hai số thực x, y bất kì thì ta luôn có hoặc x = y hoặc x < y hoặc x > y.
Những số thực lớn hơn 0 gọi là số thực dương, các số thực nhỏ hơn 0 gọi là số thực âm.
Số 0 không là số thực dương cũng không phải là số thực âm.
Việc so sánh số thực dương làm tương tự như so sánh các số hữu tỉ.

Ví dụ 1 Điền chữ số thích hợp vào (…) :

a) – 3,02 < – 3, … 1

b) – 7,5 … 8 > – 7,513 ;

c) – 0,4 … 854 < – 0,49826 ;

d) -1, … 0765 < – 1,892.

Hướng dẫn

a) – 3,02 < – 301

b) – 7,508 > – 7,513 ;

c) – 0,49854 < – 0,49826 ;

d) -1,90765 < – 1,892.

Ví dụ 2: Sắp xếp các số thực -3,5; 1;-1/3; 7,6; 0; -1,5 theo thứ tự tăng dần

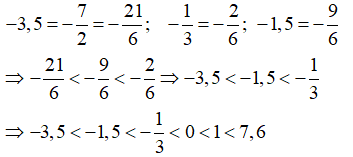
Dạng 3. Tìm số chưa biết ở trong một đẳng thức

Phương pháp giải

Cần sử dụng đến tính chất của các phép toán
Sử dụng quan hệ giữa những số hạng trong một tổng, một hiệu; quan hệ giữa các thừa số trong một tích, quan hệ giữa số bị chia, số chia và thương ở phép chia.
Sử dụng theo quy tắc dấu ngoặc, chuyển vế

Ví dụ: Tìm x, biết: 3,2.x + (-1,2).x +2,7 = -4,9 ;

Giải.

3,2. x + (-1,2).x + 2,7 = -4,9

[3,2 + (-1,2)].x + 2,7 = -4,9.

2.x + 2,7 = – 4,9.

2.x = – 4,9 – 2,7

2.x = – 7,6

x = -7,6 : 2

x = -3,8

Dạng 4: Tính giá trị biểu thức

Phương pháp giải

Thực hiện phối hợp nhuần nhuyễn phép tính cộng, trừ, nhân, chia, lũy thừa, chú ý thực hiện đúng theo thứ tự đã quy định.
Rút gọn các phân số về tối giản nhất
Chú ý vận dụng tính chất những phép toán để tính toán được thuận tiện.

Ví dụ: Tính giá trị của các biểu thức sau:

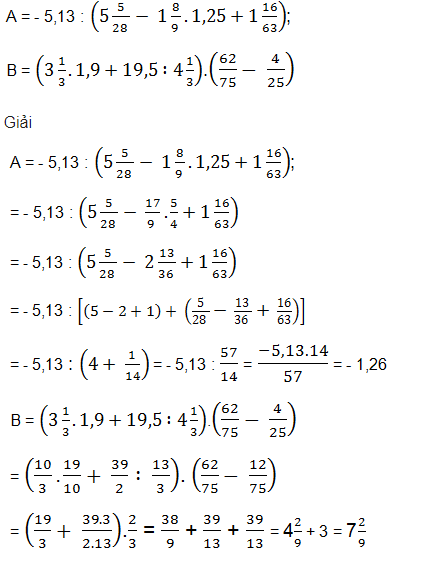
Bên trên chính là toàn bộ lý thuyết và bài tập về số thực là gì có thể giúp bạn áp dụng vào làm bài tập nhé. Hãy thường xuyên theo dõi THPT CHUYÊN LAM SƠN để được chia sẻ những kiến thức bổ ích về Toán Học, Vật Lý, Hóa Học,..bổ ích nhé