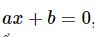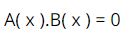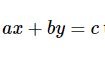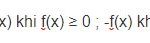Lý thuyết hàm số và phương pháp giải bài tập có lời giải từ A – Z

Trong bài viết dưới đây, THPT CHUYÊN LAM SƠN sẽ chia sẻ lý thuyết về hàm số và phương pháp giải bài tập hàm số có lời giải chi tiết trong bài viết dưới đây để các bạn cùng tham khảo nhé

• Tham khảo thêm: Số thực là gì? Tính chất của số thực và bài tập chi tiết từ A – Z

Định nghĩa hàm số

Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.

Nhận xét: Nếu đại lượng y là hàm số của đại lượng x thì mỗi giá trị của đại lượng x đều có một giá trị tương ứng duy nhất của đại lượng y ( hay mỗi giá trị của x không thể có hơn một giá trị tương ứng của đại lượng y).

Chú ý:

• Khi x thay đổi mà y luôn nhận một giá trị thì y được gọi là hàm hằng.
• Hàm số có thể được cho bằng bảng, bằng công thức,…
•  Khi y là hàm số của x ta có thể viết: y = f(x); y = g(x);…

Mặt phẳng tọa độ

Mặt phẳng tọa độ Oxy ( mặt phẳng có hệ trục tọa độ Oxy) được xác định bởi hai trục số vuông góc với nhau: trục hoành Ox và trục tung Oy; điểm O là gốc tọa độ.

Hai trục tọa độ chia mặt phẳng tọa độ thành bốn góc phần tư thứ I, II, III, IV theo thứ tự ngược chiều kim đồng hồ.

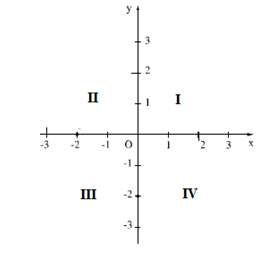
Tọa độ một điểm:

Trên mặt phẳng tọa độ:

• Mỗi điểm M xác định một cặp số (x₀; y₀). Ngược lại mỗi cặp số (x₀; y₀) xác định một điểm M
• Cặp số (x₀; y₀) gọi là tọa độ của điểm M, x₀ là hoành độ, y₀ là tung độ của điểm M.
• Điểm M có tọa độ (x₀; y₀) kí hiệu là M(x₀; y₀)

Bài tập hàm số có lời giải

Dạng 1: Tìm giá trị của hàm số tại giá trị cho trước của biến số

Phương pháp:

• Nếu hàm số được cho bằng bảng, ta tìm trong bảng giá trị của hàm số tương ứng với giá trị cho trước của biến số.
• Nếu hàm số được cho bằng công thức, ta thay giá trị đã cho của biến vào công thức và tính giá trị tương ứng của hàm số.

Ví dụ 1:Cho hàm số y = f(x) =12/x

a) Tính f(5); f(−3).

b) Hãy điền các giá trị tương ứng của hàm số vào bảng sau:

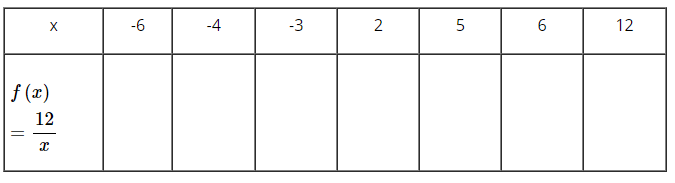
Lời giải

Ta có: y = f(x) = 12/x

a) f(5) = 12/5 = 2,4

f(−3) = 12/−3 = − 4

b) Thay lần lượt x = −6, x = −4; x = −3; x = 2 ;x = 5; x = 6;x = 12 vào công thức f(x) = 12/x ta được:

f(−6)=12/−6=−2

f(−4)=12/−4 =−3

f(−3) = 12/−3 = −4

f(2) = 12/2 = 6

f(5) = 12/5 = 2,4

f(6) = 12/6 = 2

f(12) = 12/12 = 1

x	-6	-4	-3	2	5	6	12
f(x) = 12/x	-2	-3	-4	6	2,4	2	1

Dạng 2: Viết công thức xác định hàm số

Phương pháp: Căn cứ vào sự tương quan giữa các đại lượng để lập công thức

Ví dụ: Cho hàm số y = f(x) = x² – 2. Hãy tính f(2) ; f(1) ; f(0) ; f(-1) ; f(-2)

Lời giải:

Ta có y= f(x) = x² – 2

Do đó f(2) = 2² – 2 = 4 – 2 = 2

f(1) = 1² – 2 = 1 – 2 = -1

f(0) = 0² – 2 = 0 – 2 = -2

f(-1) = (-1)² – 2 = 1 – 2 = -1

f(-2) = (-2)² – 2 = 4 – 2 = 2

Dạng 3: Viết tọa độ của điểm cho trước trên mặt phẳng tọa độ

Phương pháp:

• Từ điểm đã cho kẻ đường thẳng song song với trục tung, cắt trục hoành tại một điểm biểu diễn hoành độ của điểm đó.
• Từ điểm đã cho kẻ đường thẳng song song với trục hoành, cắt trục tung tại một điểm biểu diễn tung độ của điểm đó.
• Hoành độ và tung độ tìm được là tọa độ của điểm đã cho

Ví dụ 1: Tìm tọa độ các đỉnh của hình chữ nhật ABCD và của hình tam giác PQR trong hình20.

Lời giải

Từ các đỉnh của hình chữ nhật ABCD và các đỉnh của hình tam giác PQR ta vẽ các đường vuông góc xuống các trục Ox và Oy.

Tọa độ giao điểm của các đường vuông góc với Ox và Oy cho ta biết hoành độ và tung độ của điểm đó. Vậy tọa độ các đỉnh của hình chữ nhật ABCD là A(0,5;2); B(2;2); C(2;0); D(0,5;0).

Tọa độ các đỉnh của hình ΔPQR là: P(−3;3); Q (−1;1); R(−3;1)

Dạng 4: Biểu diễn các điểm có tọa độ cho trước trên mặt phẳng tọa độ

Phương pháp:

• Từ điểm biểu diễn hoành độ của điểm cho trước kẻ đường thẳng song song với trục tung
• Từ điểm biểu diễn tung độ của điểm cho trước kẻ đường thẳng song song với trục hoành
• Giao điểm của hai đường thẳng vừa dựng là điểm phải tìm.

Ví dụ: Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm A(−4;−1); B(−2;−1), C(−2;−3); D(−4;−3).Tứ giác ABCD là hình gì?

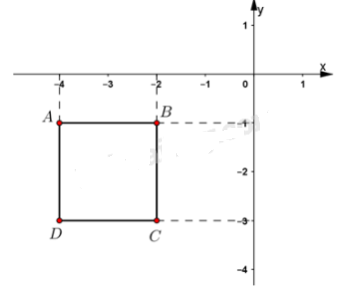
Vẽ một hệ trục tọa độ Oxy (hình vẽ) và đánh dấu các điểm như sau:

Từ tọa độ của các điểm ta vẽ các đường vuông góc với các trục Ox, Oy giao điểm của các đường vuông góc là vị trí các điểm cần đánh dấu.

Đánh dấu điểm A(−4;−1): Từ hoành độ x = −4 ta vẽ đường vuông góc với Ox và từ tung độ y =−1 ta vẽ đường vuông góc với Oy. Giao điểm hai đường vuông góc này là điểm A.

Tương tự như thế ta đánh dấu các điểm B,C,D.

Theo hình vẽ tứ giác ABCD là hình vuông vì có 4 cạnh bằng nhau và 4 góc vuông.

Sau khi đọc xong bài viết của chúng tôi các bạn có thể nắm được lý thuyết về hàm số từ đó vận dụng vào làm bài tập nhé