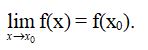Cách tính diện tích xung quanh hình trụ và ứng dụng trong thực tế

Công thức tính diện tích xung quanh và thể tích hình trụ là những công thức quan trọng trong tính toán không gian. Diện tích xung quanh hình trụ được tính bằng chu vi đường tròn đáy nhân với chiều cao, trong khi diện tích toàn phần của hình trụ bao gồm cả diện tích xung quanh và diện tích 2 đáy. Thể tích hình trụ được tính bằng chiều cao nhân với bình phương độ dài bán kính mặt đáy và số pi. Các công thức này có thể được áp dụng vào các ví dụ cụ thể để tính toán diện tích và thể tích của hình trụ.

Cách tính diện tích xung quanh hình trụ và diện tích toàn phần của hình trụ

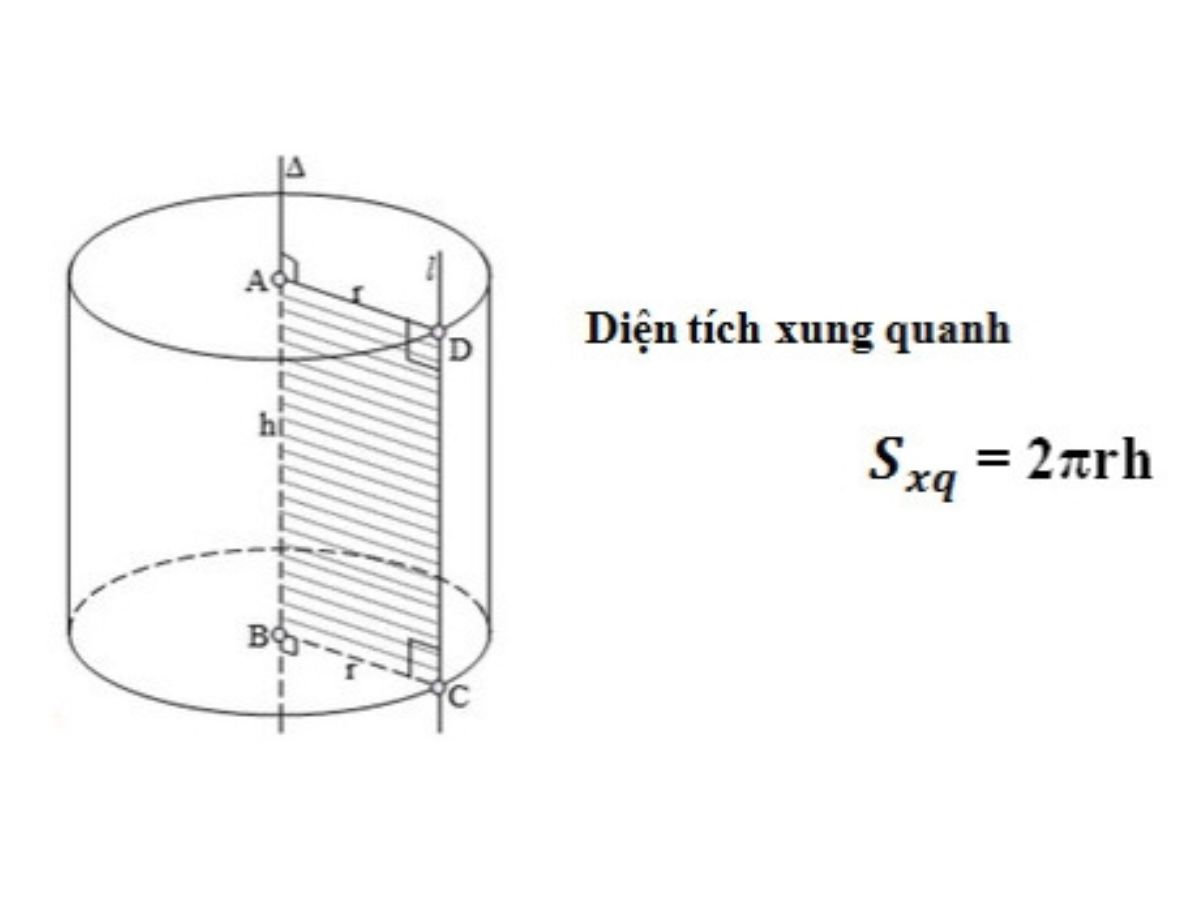
Để tính diện tích xung quanh hình trụ, ta sử dụng công thức: diện tích xung quanh = chu vi đường tròn đáy nhân với chiều cao. Với Sxung quanh là diện tích xung quanh hình trụ, r là bán kính đáy và h là chiều cao của hình trụ. Công thức này được biểu diễn như sau:

Diện tích xung quanh:

• Sxung quanh = 2πrh

Để tính diện tích toàn phần của hình trụ, ta cần cộng thêm diện tích hai đáy vào diện tích xung quanh. Công thức được biểu diễn như sau:

Diện tích toàn phần:

• Stoàn phần = Sxung quanh + 2Sđáy

Với Stoàn phần là diện tích toàn phần của hình trụ, Sđáy là diện tích hai đáy, Sxung quanh là diệc tịhc xung quahnh của hình tụ. Công thức này có thể được rút gọn thành công thức khác:

Diện tích toàn phần:

• Stoàn phần = 2πrh + 2πr² = 2πr(h + r)

Bên cạnh đó, để tính thể tích của hình trụ, ta sử dụng công thức: thể tích = diện tích đáy nhân với chiều cao. Với V là thể tích của hình trụ, Sđáy là diện tích của đáy và h là chiều cao của hình trụ. Công thức này được biểu diễn như sau:

Thể tích:

• V = Sđáy * h

Cách tính diện tích xung quanh hình trụ:

Diện tích xung quanh của hình trụ được tính bằng công thức Sxung quanh = 2πrh, trong đó r là bán kính đáy của hình trụ và h là chiều cao của hình trụ. Đây là phần diện tích bao quanh bên ngoài của hình trụ.

Ví dụ:

• Cho một hình trụ có bán kính đáy là 4 cm và chiều cao là 10 cm. Ta có thể tính diện tích xung quanh như sau:
  
  Sxung quanh = 2π(4)(10) = 80π cm².

Cách tính diện tích toàn phần của hình trụ:

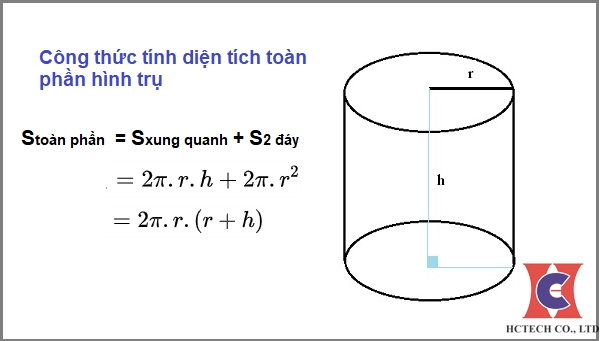
Diện tích toàn phần của hình trụ được tính bằng công thức Stoàn phần = Sxung quanh + S2đáy, trong đó Sxung quanh là diện tích xung quanh của hình trụ và S2đáy là diện tích cả hai đáy của hình trụ. Đây là tổng thể diện tích bao quanh và các đáy.

Ví dụ:

• Tiếp tục ví dụ trước, ta đã biết diện tích xung quanh là 80π cm². Giả sử diện tích đáy của hình trụ là 16π cm², ta có thể tính diện tích toàn phần như sau:
  
  Stoàn phần = 80π + 16π = 96π cm².

Cách tính thể tích của hình trụ:

Thể tích của hình trụ được tính bằng công thức V = πr²h, trong đó r là bán kính đáy của hình trụ và h là chiều cao của hình trụ. Đây là khối lượng không gian mà hình trụ chiếm.

Ví dụ:

• Tiếp tục ví dụ trước, ta đã biết bán kính đáy là 4 cm và chiều cao là 10 cm. Ta có thể tính thể tích như sau:
  
  V = π(4)²(10) = 160π cm³.

Các công thức này cung cấp cho chúng ta các phương pháp tiện lợi để tính toán diện tích và thể tích của hình trụ dựa vào các thông số như bán kính đáy và chiều cao. Việc áp dụng công thức này sẽ giúp chúng ta hiểu rõ hơn về không gian mà hình trụ chiếm và có thể áp dụng vào các bài toán thực tế.

Công thức tính diện tích toàn phần của hình trụ là gì?

Công thức tính diện tích xung quanh hình trụ

Để tính diện tích xung quanh của một hình trụ, ta sử dụng công thức: Sxung quanh = 2πrH, trong đó r là bán kính đáy và H là chiều cao của hình trụ.

Công thức tính diện tích 2 đáy của hình trụ

Điểm khác biệt giữa diện tích toàn phần và diện tích 2 đáy của hình trụ là sự có hay không có sự cộng thêm của các thành phần khác nhau. Diện tích 2 đáy của một hình trụ được tính bằng công thức Sđáy = πr^2.

Công thức tính diện tích toàn phần hình trụ

Để tính diện tích toàn phần của một hình trụ, ta sử dụng công thức Stoàn phần = Sxung quanh + 2Sđáy, trong đó Sxung quanh là diện tích xung quanh và Sđáy là diện tích 2 đáy.

Tính diện tích toàn phần của hình trụ khi biết diện tích xung quanh và diện tích 2 đáy.

Để tính diện tích toàn phần của hình trụ khi đã biết diện tích xung quanh và diện tích 2 đáy, ta cần áp dụng các công thức sau:

1. Công thức tính diện tích xung quanh hình trụ: Diện tích xung quanh (Sxung quanh) của hình trụ bằng chu vi đường tròn đáy nhân với chiều cao (h). Công thức này có dạng: Sxung quanh = 2πr×h.

2. Công thức tính diện tích 2 đáy (S2đáy): Diện tích 2 đáy (S2đáy) của hình trụ là bằng tổng hai lần diện tích một mặt đáy, với công thức S2đáy = 2πr^2.

3. Công thức tính diện tích toàn phần (Stoàn phần): Diện tích toàn phần (Stoàn phần) của hình trụ là tổng của diện tích xung quanh (Sxung quanh) và diện tích 2 đáy (S2đáy), có công thức Stoàn phần = Sxung quanh + S2đáy.

Với các công thức trên, ta có thể tính được diện tích toàn phần của hình trụ khi đã biết diện tích xung quanh và diện tích 2 đáy.

Định nghĩa và công thức tính thể tích của hình trụ là gì?

Định nghĩa hình trụ:

Hình trụ là một hình học có hai đáy đồng dạng và song song nhau, được kết nối bởi một bề mặt cong không chỉ giới hạn ở đường viền của hai đáy. Hai đáy của hình trụ là các hình tròn có tâm và cùng một đường kính. Chiều cao của hình trụ là khoảng cách từ một đáy đến đỉnh của hình trụ.

Công thức tính thể tích của hình trụ:

Thể tích (V) của một hình trụ được tính bằng cách nhân diện tích bên căn cứ (S) với chiều cao (h) của hình trụ.
Công thức: V = S x h
Trong đó:
– V là thể tích của hình trụ
– S là diện tích căn cứ (diện tích đáy)
– h là chiều cao của hình trụ

Cách tính thể tích hình trụ khi biết chiều cao và bán kính đáy.

Thể tích của một hình trụ có thể được tính bằng cách nhân diện tích đáy (Sđáy) với chiều cao (h). Diện tích đáy của hình trụ có thể được tính bằng công thức Sđáy = π * r², trong đó r là bán kính đáy. Vì vậy, công thức để tính thể tích V của một hình trụ khi biết chiều cao và bán kính đáy là: V = Sđáy * h = π * r² * h. Đây là công thức cơ bản để xác định thể tích của một hình trụ.

Một ví dụ điển hình cho việc áp dụng công thức này là khi ta có một hình trụ có bán kính đáy là 3 cm và chiều cao là 5 cm. Đầu tiên, ta sẽ tính diện tích đáy theo công thức Sđáy = π * r² = 3.14 * 3² = 28.26 cm². Sau đó, ta nhân diện tích đáy với chiều cao để tìm ra thể tích: V = Sđáy * h = 28.26 cm² * 5 cm = 141.3 cm³.

Với việc biết công thức tính thể tích hình trụ khi biết chiều cao và bán kính đáy, ta có thể áp dụng vào các bài toán thực tế như trong ngành xây dựng, sản xuất đồ gia dụng chứa chất lỏng, v.v.

Cách tính diện tích hình trụ

Diện tích hình trụ bao gồm: diện tích xung quanh và diện tích toàn phần. Mỗi loại diện tích sẽ có công thức tính toán riêng.

Công thức tính diện tích xung quanh hình trụ

Công thức tính diện tích xung quanh hình trụ là chu vi đường tròn đáy nhân với chiều cao.
Sxung quanh = 2πr * h
– Sxung quanh: Diện tích xung quanh hình trụ
– r: bán kính đáy của hình trụ
– h: chiều cao của hình trụ

Công thức tính diện tích toàn phần của hình trụ

Công thức tính diện tích toàn phần của hình trụ là tổng của diện tích xung quanh và diện tích hai đáy.
Stoàn phần = Sxung quanh + S2đáy
– Stoàn phần: Diện tích toàn phần của hình trụ
– Sxung quanh: Diện tích xung quanh hình trụ
– S2đáy: Diện tích hai đáy của hình trụ

Cách khác để tính diện tích toàn phần của hình trụ?

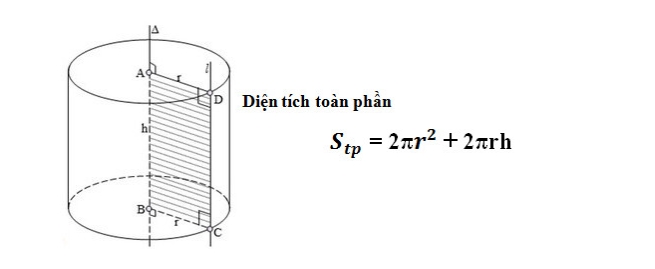
Có một cách khác để tính diện tích toàn phần của hình trụ. Ta có thể sử dụng công thức tổng quát để tính diện tích toàn phần.
Stoàn phần = 2πr(h + r)
– Stoàn phần: Diện tích toàn phần của hình trụ
– r: bán kính đáy của hình trụ
– h: chiều cao của hình trụ

Với cách này, ta không cần phải tính riêng diện tích xung quanh và diện tích hai đáy, mà chỉ cần áp dụng công thức tổng quát và thay vào giá trị tương ứng của bán kính và chiều cao.

Tổng kết, diện tích xung quanh hình trụ là tổng diện tích của hồi quy và hai đáy của hình trụ. Để tính được diện tích này, ta cần biết chiều cao và bán kính của hình trụ. Công thức tính diện tích xung quanh hình trụ là 2πr * h, trong đó r là bán kính và h là chiều cao. Việc tính toán diện tích xung quanh hình trụ giúp chúng ta hiểu rõ về không gian và cấu trúc của một đối tượng ba chiều trong toán học.