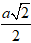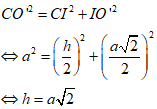Công thức tính diện tích, thể tích hình trụ kèm VD minh họa

Ta bắt gặp nhiều vật trong cuộc sống có dạng hình trụ nhưng ít ai biết công thức tính thể tích hình trụ? Diện tích xung quanh hình trụ? Diện tích toàn phần hình trụ? Mặc dù những công thức này được ứng dụng rất nhiều trong cuộc sống. Nếu bạn đang quan tâm thì xem bài viết chi tiết dưới đây để hiểu thêm

Tham khảo thêm:

• Công thức tính đường cao trong tam giác thường, vuông, đều, cân từ A- Z
• Công thức tính đường chéo hình vuông và bài tập có lời giải chuẩn 100%
• Công thức tính nửa chu vi hình chữ nhật và bài tập có lời giải từ A – Z

Hình trụ là gì?

Hình trụ tròn là một loại hình học không gian cơ bản được giới hạn bởi mặt trụ và hai đáy là hai đường tròn bằng nhau.

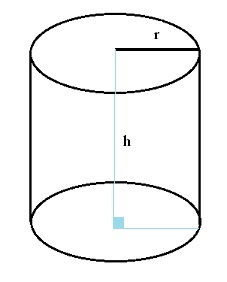
Tính chất của hình trụ

• Hình trụ có hai mặt đáy bằng nhau
• Hai cạnh song song nhau có độ dài bằng nhau
• Trục tọa độ của hình trụ được nối từ hai tâm của hai mặt đáy

Công thức tính diện tích xung quanh hình trụ

Diện tích xung quanh hình trụ chỉ bao gồm diện tích mặt xung quanh, bao quanh hình trụ tròn, không gồm diện tích hai đáy.

 S_xq = 2.π.r.h

Trong đó:

• r: Bán kính hình trụ.
• h: Chiều cao nối từ đáy tới đỉnh hình trụ.
• π: 3.1415925359

Công thức tính diện tích toàn phần hình trụ

Để tính diện tích toàn phần hình trụ các bạn có thể tính lần lượt diện tích đường tròn 2 đáy và diện tích xung quanh hình trụ sau đó tính tổng hai diện tích sẽ được diện tích toàn phần

Stp = Sxq + Sđ = 2πrh + 2πr²

Trong đó:

• S_tp: Diện tích toàn phần hình trụ
• S_xq: Diện tích xung quanh hình trụ
• S_đáy: Diện tích hai đáy

Công thức tính thể tích hình trụ

Muốn tính thể tích của hình trụ, ta lấy chiều cao nhân với bình phương độ dài bán kính hình tròn mặt đáy hình trụ và số pi

V = πr² h

Trong đó:

• V là kí hiệu thể tích
• r là bán kính hình tròn mặt đáy hình trụ
• h là chiều cao của hình trụ
• π là hằng số ( π = 3, 14)

Các dạng toán hường gặp của diện tích xung quanh hình trụ

Bài 1: Cho một hình trụ có bán kính đường tròn đáy là 6 cm , chiều cao từ đỉnh đến đáy dà 8 cm. Hỏi diện tích xung quanh và diện tích toàn phần của hình trụ bằng bao nhiêu?

Giải:

Theo công thức ta có bán đường tròn đáy r = 6 cm và chiều cao của hình trụ h = 8 cm . Suy ra ta có công thức tính diện tích xung quanh hình trụ và diện tích toàn phần hình trụ bằng:

Diện tích xung quanh hình trụ = 2 .π .r .h = 2 . π . 6 *.8 = ~ 301 cm2
Diện tích toàn phần hình trụ = 2 . π . r . (r + h) = 2 . π . 6 . (6 + 8) = ~ 527 cm2.

Bài 2: Cho hình trụ có bán kính đáy R = 4 (cm) và chiều cao h = 5 (cm). Diện tích xung quanh của hình trụ là:

Giải:

Diện tích xung quanh của hình trụ là:

S_xq = 2.π.R.h = 2π.4.5 = 40π (cm²)

Bài 3: Tính diện tích xung quanh của một hình trụ có chu vi đường tròn đáy là 4π và chiều cao h =2.

Giải:

Bài 4: Trong không gian, cho hình chữ nhật ABCD có AB = 1 và AD = 2. Gọi M,N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần Stp của hình trụ đó

Giải:

Khi quay hình chữ nhật quanh trục MN ta được hình trụ có:

+ chiều cao: h = AB = 1 .

+ bán kính đường tròn đáy là r = Dạng bài tập về hình trụ, mặt trụ cực hay, có lời giải = 1

Do đó,diện tích toàn phần của hình trụ đó là:

Stp = 2πrh + 2πr² = 2π.1.1 + 2π.12 = 4π

Bài 5: Một hình thang vuông ABCD có đường cao AD = π, đáy nhỏ AB = π , đáy lớn CD = 2π . Cho hình thang quay quanh CD, ta được khối tròn xoay có thể tích bằng

Giải:

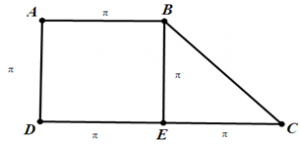
Khi quay hình thang quanh CD ta được khối tròn xoay gồm 2 phần:

+ Khối V₁ là khối trụ có bán kính đáy AD = π và chiều cao AB = π nên thể tích khối trụ tạo thành là: V₁ = π.π².π = π⁴

+ Khối V₂ là khối nón có bán kính đường tròn đáy là BE = π và đường cao BC = π nên thể tích của khối nón là:

V2= 1/3.π.π².π = 1/3 π⁴

Vậy thể tích khối tròn xoay cần tính là : V = V1 + V2= 4/3 π⁴

Bài 6: Cho hình chữ nhật ABCD có AB = a và góc 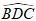 = 30⁰ . Quay hình chữ nhật này xung quanh cạnh AD. Diện tích xung quanh của hình trụ được tạo thành là:

Giải:

+ Khi quay hình chữ nhật này xung quanh cạnh AD ta được hình trụ như hình vẽ.

Hình trụ tạo thành có:

+ Bán kính đường tròn đáy là r = AB = a

+ Đường cao của hình trụ là:
h = BC = CD.tan30⁰ =

=

Suy ra, diện tích xung quanh của hình trụ tạo thành là:

Bài 7: Cho hình trụ có hai đáy là hình tròn (O) và (O’). Trên hai đường tròn lấy hai điểm A, B sao cho góc giữa AB và mặt phẳng chứa đường tròn đáy bằng 45⁰ và khoảng cách đến trục OO’ bằng  . Biết bán kính đáy bằng a, tính thể tích của

Giải:

Đặt OO’ = h. Gọi I, E, D lần lượt là trung điểm của BC, BA, OO’.

Ta có: d(AB,OO’) = ED = IO’ = 

Tam giác ABC vuông tại C có B = 45⁰
⇒ tam giác ABC vuông cân

⇒ BC = AC = h

Ta có:

Thể tích khối trụ là: V = πa².a √2 = πa³√2

Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình