Cách chứng minh hai đường thẳng vuông góc và bài tập có lời giải chia tiết 100%
Trong bài viết hôm nay chúng tui tổng hợp các bài tập hai đường thẳng vuông góc, đồng thời đưa ra những kiến thức lý thuyết nền căn bản trong chuyên đề hai đường thẳng vuông góc chi tiết trong bài viết dưới đây, mời các bạn cùng đón xem
Tham khảo thêm:
- Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp và bài tập có lời giải
- Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử và bài tâp có lời giải từ A- Z
- Phân tích đa thức thành nhân tử chung và bài tập có lời giải từ A- Z
Nội Dung
Hai đường thẳng vuông góc là gì?
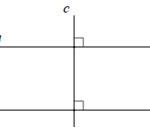
Hai đường thẳng xx’ và yy’ cắt nhau. Nếu trong các góc tạo thành có một góc vuông thì hai đường thẳng đó gọi là hai đường thẳng vuông góc và kí hiệu xx’ ⊥ yy’
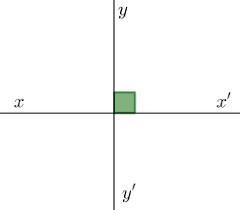
Tính chất: Có một và chỉ một đường thẳng a’ đi qua điểm O cho trước và vuông góc với đường thẳng a cho trước.
Đường trung trực của đoạn thẳng
Đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng được gọi là đường trung trực của đoạn thẳng ấy.
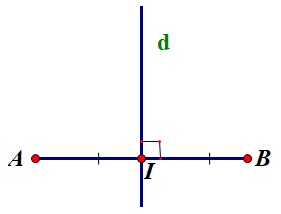
Ta có xy vuông góc với đoạn thẳng AB tại I là trung điểm của AB nên xy là đường trung trực của đoạn thẳng AB
Các dạng toán liên quan đến hai đường thằng vuông góc
Bài 1: Chọn hai đường thẳng aa’ và bb’ vuông góc với nhau tại O. Hãy chỉ ra câu sai trong các câu sau:
Giải:
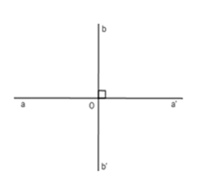
Hai đường thẳng và vuông góc với nhau tại nên:
+ ∠aOb = 90° nên B đúng.
+ aa’ và bb’ vuông góc với nhau nên aa’ và bb’ cắt nhau nên C sai.
+ ∠a’Ob = ∠ a’Ob’ = 90° ⇒ aa’ là đường phân giác của góc bẹt bOb’ nên D đúng.
+ ∠b’Oa’ = 90° nên A đúng.
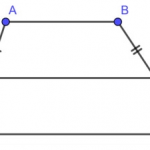
Bài 2: Cho đoạn thẳng MN = 6 cm. Trên tia MN lấy điểm P sao cho MP = 1 cm, trên tia NM lấy điểm Q sao cho NQ = 1 cm. Khi đó:
Giải:
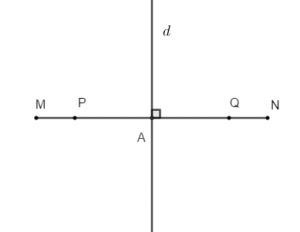
+ Trên tia MN có:
MN = 6 cm; MP = 1 cm
Suy ra P nằm giữa M và N (do 6 > 1)
⇒ MP + PN = MN ⇒ PN = MN – MP = 6 – 1 = 5 cm
+ Trên tia NM có:
NM = 6 cm; NQ = 1 cm
Suy ra Q nằm giữa M và N (do 6 > 1)
⇒ NQ + QM = NM ⇒ QM = NM – NQ = 6 – 1 = 5 cm
Do đó: PN = QM (= 5 cm) A đúng
+ Gọi A là trung điểm của đoạn thẳng MN ⇒ AM = AN = 1/2 MN = 3 cm
Gọi d là đường thẳng đi qua A và vuông góc với MN tại A
Do đó d là đường trung trực của đoạn thẳng MN
Vì P và Q đều thuộc MN, nên suy ra d ⊥ PQ (1) ⇒ B đúng
+ Trên tia MN có MA = 3 cm; MP = 1 cm
Suy ra P nằm giữa M và A ⇒ MP + PA = MA ⇒ PA = MA – MP = 3 – 1 = 2 cm
Chứng minh tương tự ta có: NQ + QA = NA ⇒ QA = NA – NQ = 3 – 1 = 2 cm
Do đó: PA = QA, mà P, Q, A thẳng hàng (do P, Q, A đều thuộc MN)
Suy ra A là trung điểm của PQ (2)
Từ (1) và (2) suy ra d là đường trung trực của đoạn thẳng PQ
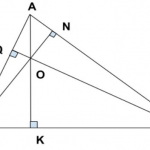
Bài 3: Cho ΔABC vuông tại A, M là trung điểm của AC. Gọi D, E lần lượt là hình chiếu của A và C xuống đường thẳng BM. So sánh BD + BE và AB
Giải:
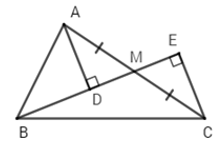
Vì ΔABM vuông tại A (gt) nên BA < BM (quan hệ giữa đường vuông góc và đường xiên)
Mà BM = BD + DM ⇒ BA < BD + DM (1)
Mặt khác: BM = BE – ME ⇒ BA < BE – ME (2)
Cộng hai vế của (1) và (2) ta được: 2BA < BD + BE + MD – ME (3)
Vì M là trung điểm của AC (gt) ⇒ AM = MC (tính chất trung điểm)
Xét tam giác vuông ADM và tam giác vuông CEM có:
AM = MC (cmt)
∠AMD = ∠EMC (đối đỉnh)
Do đó: ΔADM = ΔCEM (cạnh huyền – góc nhọn)
⇒ MD = ME (4) (2 cạnh tương ứng)
Từ (3) và (4) ⇒ BD + BE > 2AB
Bài 4: Cho tam giác ABC nhọn. Vẽ tia Ax nằm trong góc BAC, Ax cắt BC ở M. Gọi E và F theo thứ tự là hình chiếu của B và C trên tia Ax. So sánh BE + CF với BC
Giải;
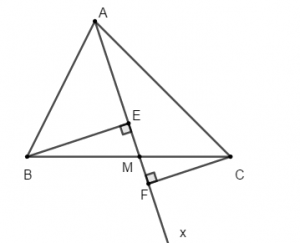

Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình