Tính thể tích khối nón được giới hạn bởi hình nón: Bài toán và cách tính

Hình nón là một hình học có đường cao và bán kính đáy đã được cho trước. Bằng cách sử dụng các công thức tính diện tích và thể tích của hình nón, chúng ta có thể tính toán được giá trị này.

Nội Dung

1. Tính thể tích của khối nón được giới hạn bởi hình nón có đường cao 20cm và bán kính đáy 25cm.

Để tính thể tích của khối nón, ta sử dụng công thức:

V = (1/3) * π * r^2 * h

Với V là thể tích của khối nón, π là số pi (khoảng 3.14), r là bán kính đáy của hình nón và h là đường cao của hình nón.

Áp dụng vào bài toán này, ta có:

V = (1/3) * π * (25^2) * 20 = 52,359 cm^3

Công thức:

V = (1/3) * π * r^2 * h
Với V là thể tích của khối nón
π là số pi (khoảng 3.14)
r là bán kính đáy của hình nón
h là đường cao của hình nón

2. Diện tích xung quanh của hình nón đó là bao nhiêu?

Diện tích xung quanh của một hình nón được tính bằng công thức:

S = π * r * l

Với S là diện tích xung quanh của hình nón, π là số pi (khoảng 3.14), r là bán kính đáy của hình nón và l là đường tròn xung quanh hình nón được gọi là chu vi đáy của hình nón.

Áp dụng vào bài toán này, ta có:

S = π * 25 * l

Công thức:

S = π * r * l
Với S là diện tích xung quanh của hình nón
π là số pi (khoảng 3.14)
r là bán kính đáy của hình nón
l là đường tròn xung quanh hình nón được gọi là chu vi đáy của hình nón

3. Hãy tính khoảng cách giữa mặt phẳng AB và trục của hình trụ khi góc giữa đường thẳng AB và trục là 30o.

Khi góc giữa một đường thẳng và trục của một hình trụ được cho, ta có thể tính được khoảng cách giữa hai mặt phẳng tạo bởi đường thẳng và trục.

Trong trường hợp này, góc giữa đường thẳng AB và trục của hình trụ là 30o. Để tính khoảng cách giữa mặt phẳng AB và trục, ta sử dụng công thức:

d = r * tan(θ)

Với d là khoảng cách giữa hai mặt phẳng, r là bán kính đáy của hình trụ và θ là góc giữa đường thẳng và trục.

Áp dụng vào bài toán này, ta có:

d = 25 * tan(30o) = 14.43 cm

Công thức:

d = r * tan(θ)
Với d là khoảng cách giữa hai mặt phẳng
r là bán kính đáy của hình trụ
θ là góc giữa đường thẳng và trục

4. Cắt khối trụ có bán kính đáy 5cm và khoảng cách giữa hai đáy là 7cm bởi một mặt phẳng song song với trục, diện tích thiết diện được tạo nên là bao nhiêu?

Để tính diện tích thiết diện của khối trụ khi cắt bởi một mặt phẳng song song với trục, ta cần biết rằng thiết diện này sẽ tạo thành một hình tròn.

Áp dụng công thức tính diện tích hình tròn: S = πr^2, trong đó S là diện tích, r là bán kính.

Với khối trụ này, chúng ta đã biết rằng bán kính đáy là 5cm. Vì mặt phẳng cắt đi qua trục và khoảng cách giữa hai đáy là 7cm, nên khoảng cách từ mặt phẳng cắt tới các đáy sẽ là (7/2)cm = 3.5cm.

Do đó, bán kính của thiết diện được tạo nên sẽ là bán kính của đáy + khoảng cách từ mặt phẳng cắt tới đáy: r’ = 5cm + 3.5cm = 8.5cm.

Áp dụng công thức, diện tích thiết diện là: S = πr’^2 = 3.14 * (8.5cm)^2 = 226.865 cm^2.

Công thức:

Diện tích hình tròn: S = πr^2

Kết quả:

Diện tích thiết diện của khối trụ khi cắt bởi một mặt phẳng song song với trục là 226.865 cm^2.

5. Hình nón có bán kính r và góc ở đỉnh là bao nhiêu nếu cắt mặt xung quanh của hình nón xoay dọc theo một đường sinh rồi trải ra trên một mặt phẳng để tạo thành một nửa hình tròn bán kính R?

Để tìm góc ở đỉnh và bán kính của hình nón, chúng ta cần biết rằng khi cắt mặt xung quanh của hình nón xoay dọc theo một đường sinh, sẽ tạo thành một nửa hình tròn.

Áp dụng công thức tính diện tích nửa hình tròn: S = (πR^2)/2, trong đó S là diện tích, R là bán kính.

Với hình nón này, chúng ta đã biết rằng bán kính đáy là r. Khi cắt mặt xung quanh và trải ra thành nửa hình tròn, ta sẽ có bán kính của nửa hình tròn là R.

Theo phép xoay của một hình tròn, để tạo ra nửa hình tròn từ đường sinh, góc ở đỉnh của hình nón sẽ là 90 độ (góc giữa hai phân kỳ dương của đường sinh).

Do đó, góc ở đỉnh và bán kính của hình nón lần lượt là: α = 90 độ và R = r.

Công thức:

Diện tích nửa hình tròn: S = (πR^2)/2

Kết quả:

Góc ở đỉnh của hình nón khi cắt mặt xung quanh và trải ra thành một nửa hình tròn là 90 độ.
Bán kính của hình nón vẫn giữ nguyên như bán kính ban đầu: R = r.

6. Tính diện tích xung quanh và thể tích của khối trụ có hai đáy là hai hình tròn ngoại tiếp hai hình vuông.

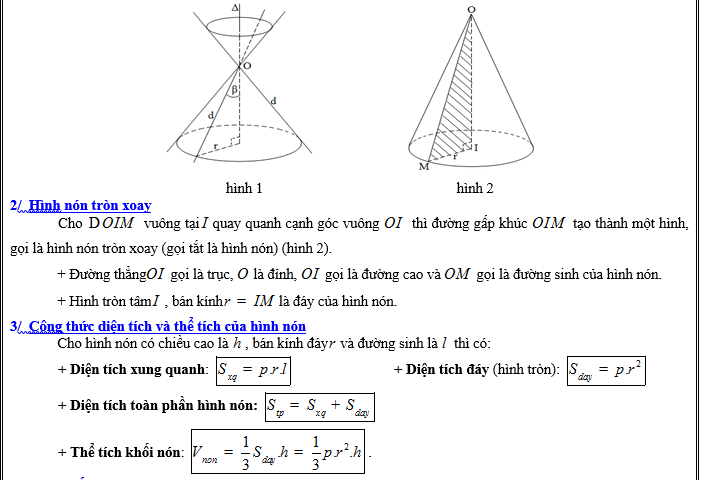
Để tính diện tích xung quanh và thể tích của khối trụ, chúng ta cần biết rằng khối trụ này có hai đáy là hai hình tròn ngoại tiếp hai hình vuông.

Áp dụng công thức tính diện tích xung quanh và thể tích của khối trụ:

Diện tích xung quanh: Sxq = 2πrh
Thể tích: V = πr^2h

Với khối trụ này, chúng ta đã biết rằng các đỉnh của hình vuông chính là các điểm nằm trên đường tròn đáy. Vì các điểm nằm trong một mặt phẳng song song với trục, nên bán kính của đường tròn đáy luôn bằng chiều cao của hình vuông: r = h.

Do đó, công thức diện tích xung quanh và thể tích của khối trụ sẽ được viết lại thành:

Diện tích xung quanh: Sxq = 2πrh = 2πrh = 4πr^2
Thể tích: V = πr^2h = πr^3

Công thức:

Diện tích xung quanh: Sxq = 2πrh hoặc 4πr^2
Thể tích: V = πr^2h hoặc πr^3

Kết quả:

Diện tích xung quanh của khối trụ có hai đáy là hai hình tròn ngoại tiếp hai hình vuông là 4πr^2.
Thể tích của khối trụ là πr^3.

7. Đặt tên cho các hình tròn hoặc khối tròn xoay sinh ra khi quay quanh các điểm trong của một hình chữ nhật qua một đường thẳng chứa một cạnh.

Khi quay quanh các điểm trong của một hình chữ nhật qua một đường thẳng, ta sẽ tạo ra các hình tròn hoặc khối tròn xoay. Các hình này có các tên riêng phụ thuộc vào vị trí và cạnh liên quan đến việc xoay.

Dựa vào vị trí của cạnh:

Nếu cạnh được sử dụng để quay là cạnh nằm ngang, ta gọi các hình tròn hoặc khối tròn xoay sinh ra là “hình tròn xoay theo chiều dọc”.
Nếu cạnh được sử dụng để quay là cạnh nằm dọc, ta gọi các hình tròn hoặc khối tròn xoay sinh ra là “hình tròn xoay theo chiều ngang”.

Dựa vào vị trí của điểm quay:

Nếu điểm quay là một đỉnh của hình chữ nhật, ta gọi các hình tròn hoặc khối tròn xoay sinh ra là “hình tròn xoay xung quanh đỉnh”.
Nếu điểm quay là một điểm nằm trong cạnh của hình chữ nhật, ta gọi các hình tròn hoặc khối tròn xoay sinh ra là “hình tròn xoay xung quanh điểm trong cạnh”.

Ví dụ: Nếu chúng ta có một hình chữ nhật ABCD với cạnh AB là cạnh được sử dụng để quay và B là điểm quay. Khi chúng ta tiến hành quay AB qua B, chúng ta sẽ tạo ra một “hình tròn xoay theo chiều dọc” và “hình tròn xoay xung quanh điểm trong cạnh”.

8. Diện tích tam giác SBC trong hình nón khi góc giữa hai mặt phẳng SBC và mặt phẳng chứa đáy là 60o.

Để tính diện tích tam giác SBC trong hình nón, chúng ta cần biết rằng góc giữa hai mặt phẳng SBC (mặt nghiêng) và mặt phẳng chứa đáy của hình nón là 60 độ.

Áp dụng công thức diện tích tam giác: S = 0.5 * a * b * sin(γ), trong đó S là diện tích, a và b là chiều dài hai cạnh của tam giác, γ là góc được tạo bởi hai cạnh đó.

Với tam giác SBC, chúng ta đã biết rằng SB và BC là các cạnh của tam giác, và góc γ sẽ là góc giữa hai mặt phẳng. Do đó, công thức diện tích tam giác sẽ được viết lại thành:

S = 0.5 * SB * BC * sin(γ)

Theo yêu cầu câu hỏi, thông tin cho biết góc γ (góc giữa hai mặt phẳng) là 60 độ.

Công thức:

Diện tích tam giác: S = 0.5 * a * b * sin(γ)

Kết quả:

Diện tích của tam giác SBC trong hình nón khi góc giữa hai mặt phẳng SBC và mặt phẳng chứa đáy là 60 độ là (0.5 * SB * BC * sin(60)) cm^2.

9. Tính diện tích xung quanh của hình trụ khi cạnh huyền của tam giác vuông cân được tạo bởi mặt phẳng cắt hình nón đỉnh S bằng a√2.

Để tính diện tích xung quanh của hình trụ, chúng ta cần biết rằng cạnh huyền của tam giác vuông cân được tạo bởi mặt phẳng cắt hình nón đỉnh S luôn bằng a√2.

Áp dụng công thức tính diện tích xung quanh của hình trụ: S = 2πrh, trong đó S là diện tích, r là bán kính, và h là chiều cao.

Với thông tin đã cho, ta có được chiều cao của khối trụ sẽ bằng cạnh huyền của tam giác vuông cân: h = a√2.

Do đó, công thức tính diện tích xung quanh của hình trụ sẽ được viết lại thành:

S = 2πr(a√2)

Công thức:

Diện tích xung quanh của hình trụ: S = 2πrh

Kết quả:

Diện tích xung quanh của hình trụ khi cạnh huyền của tam giác vuông cân được tạo bởi mặt phẳng cắt hình nón đỉnh S bằng a√2 là 2πra√2.

10. Tính thể tích khối nón được tạo thành từ hình nón có đường cao 20cm và bán kính đáy 25cm.

Để tính thể tích khối nón, chúng ta cần biết rằng khối nón này có đường cao là 20cm và bán kính đáy là 25cm.

Áp dụng công thức tính thể tích khối nón: V = (1/3) * πr^2h, trong đó V là thể tích, r là bán kính, và h là chiều cao.

Với thông tin đã cho, ta có được bán kính của khối nón là 25cm và chiều cao là 20cm.

Do đó, công thức tính thể tích của khối nón sẽ được viết lại thành:

V = (1/3) * π(25^2)* 20

Công thức:

Thể tích khối nón: V = (1/3) * πr^2h

Kết quả:

Thể tích của khối nón được tạo thành từ hình nón có đường cao 20cm và bán kính đáy 25cm là (1/3) * π(25^2)* 20 cm^3.

Trong bài viết này, chúng ta đã tìm hiểu về các khái niệm và công thức tính thể tích của hình nón. Thể tích khối nón được giới hạn bởi hình nón có rất nhiều ứng dụng trong thực tế, từ ngành xây dựng đến công nghệ thông tin. Việc hiểu và áp dụng công thức tính thể tích này sẽ giúp chúng ta giải quyết một số bài toán trong cuộc sống hàng ngày một cách khoa học và chính xác.