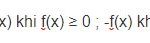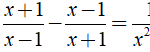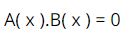Phương pháp phân tích đa thức dùng hằng đẳng thức và bài tập chuẩn 100%

Bài viết bao gồm cả lý thuyết và bài tập về phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức. Phần lý thuyết có đầy đủ các công thức và tính chất các em đã được học để áp dụng làm các bài tập. Các bài tập đều có hướng dẫn giải giúp các em có hướng làm bài và vận dụng tốt để làm những bài sau.

Tham khảo thêm:

Nội Dung

7 hằng đẳng thức đáng nhớ

Ta sử dụng các hằng đẳng thức đáng nhớ đã học để thực hiện phép phân tích đa thức thành nhân tử.

(A + B)² = A² + 2AB + B²
(A – B)² = A² – 2AB + B²
A² – B² = (A – B)(A + B)
(A + B)³ = A³ + 3²B +3AB² + B³
(A – B)³ = A³ – 3A²B +3AB² – B³
A³ + B³ = (A + B)(A² -AB + B²)
A³ – B³ = (A – B)(A² +AB + B²)

Chú ý: Khi áp dụng phương pháp dùng hằng đẳng thức để phân tích đa thức thành nhân tử, ta cần lưu ý:

Trước tiên nhận xét xem các hạng tử của đa thức có chứa nhân tử chung không ? Nếu có thì áp dụng phương pháp đặt thành nhân tử chung.
Nếu không thì xét xem có thể áp dụng hằng đẳng thức đáng nhớ để phân tích thành nhân tử hay không ?

Các dạng toán thường gặp

Dạng 1: Phân tích đa thức thành nhân tử

Phương pháp: Ta sử dụng các hằng đẳng thức đã học để phân tích đa thức đã cho thành nhân tử.

Ví dụ 1: Phân tích đa thức sau thành nhân tử:

a, Ta có: 9x² – 1 = ( 3x )² – 1 = ( 3x – 1 )( 3x + 1 )

b, Ta có: 4x² – 25 = (2x)² – 5² = (2x + 5)(2x – 5)

c, Ta có: x⁶ – y⁶ = (x³)² – (y³)² = (x² + y³)(x³ – y³)

= (x + y)(x² – xy + y)(x – y)(x²+ xy + y²)

d, Ta có : x³y³ + 6x²y² + 12xy + 8 = (xy)³ + 3(xy)².2 + 3xy.2² + 2³ = (xy + 2)³

Ví dụ 2: Phân tích đa thức sau thành nhân tử:

a, Ta có (5x – 4)² – 49x² = (5x – 4)² – (7x)²

= (5x – 4 + 7x)(5x – 4 – 7x)

= (12x – 4)(-2x – 4) = 4.(3x – 1).(-2)(x + 2)

= -8(3x – 1)(x + 2)

b, Ta có (3x – 2y)² – (2x – 3y)² = (3x – 2y + 2x – 3y)(3x – 2y – (2x – 3y))

= (5x – 5y)(3x – 2y – 2x + 3y) = 5(x – y)(x + y)

c, Ta có (a² + 9)² – 36a² = (a² + 9)² – (6a)²

= (a² + 9 + 6a)(a² + 9 – 6a) = (a + 3)²(a – 3)²

d, Ta có x⁶ – y⁶ = (x³)² – (y³)² = (x³ + y³)(x³ – y³)

= (x + y)(x² – xy + y²)(x – y)(x² + xy + y²)

Dạng 2: Tìm x

Phương pháp: Ta sử dụng các hằng đẳng thức đã học để phân tích đa thức đã cho thành nhân tử.

Từ đó đưa về dạng tìm x thường gặp như A. B = 0 ⇒ A= 0; B= 0

Ví dụ: Tìm x biết:

a, Ta có: 16x² – 9(x + 1)² = 0

⇔ (4x)² − [3 (x + 1)]² = 0

⇔ (4x)² − (3x + 3)² = 0

⇔ [4x − (3x + 3)] [4x + (3x + 3)] = 0

⇔ (4x − 3x − 3)(4x + 3x + 3) = 0

⇔ (x − 3)(7x + 3) = 0

Đáp số: x = 3; x= -3/7

b, Ta có 5x² – 10x + 5 = 0

⇔ 5(x² – 2x + 1) = 0

⇔ 5(x – 1)² = 0

⇔ x – 1 = 0

⇔ x = 1

Vậy x = 1

c, Ta có (2x – 5)² – 4(x – 2)² = 0

⇔ (2x – 5)² – [2(x – 2)]² = 0

⇔ (2x – 5)² – (2x – 4)² = 0

⇔ (2x – 5 + 2x – 4)(2x – 5 – 2x + 4) = 0

⇔ (4x – 9).(-1) = 0

⇔ -4x + 9 = 0

⇔ 4x = 9

⇔ x = 9/4

Dạng 3: Tính giá trị biểu thức thỏa mãn điều kiện cho trước

Phương pháp: Ta biến đổi biểu thức đã cho để có thể sử dụng được điều kiện ở giả thiết. Từ đó tính giá trị biểu thức.

Ví dụ: Tìm điều kiện của biến sau để các phân thức sau có nghĩa

Để phân thức có nghĩa:

x² + 3x – 4 ≠ 0

⇔ (x + 4)(x – 1) ≠ 0

⇔ x ≠ -4 và x ≠ 1

Vậy điều kiện để phân thức có nghĩa là x ≠ – 4 và x ≠ 1

Ví dụ 2: Cho (x + y)³ – (x – y)³ = A.y(Bx² + Cy²), biết A, B, C là các số nguyên. Khi đó A + B + C bằng

Ta có (x + y)³ – (x – y)³

= [x + y – (x – y)][(x + y)² + (x + y)(x – y) + (x – y)²]

= (x + y – x + y)(x² + 2xy + y² + x² – y² + x² – 2xy + y²)

= 2y(3x² + y²) ⇒ A = 2; B = 3; C = 1

Suy ra A + B + C = 2+ 3 + 1 = 6

Ví dụ 3: Cho x⁶ – 1 = (x + A)(x + B)(x⁴ + x² + C), biết A, B, C là các số nguyên. Khi đó A + B + C bằng

Ta có x⁶ – 1 = (x²)³ – 1 = (x² – 1)(x⁴ + x² + 1)

= (x – 1)(x + 1)(x⁴ + x² + 1)

⇒ A = -1; B = C = 1

Suy ra A + B + C = -1 + 1 + 1 = 1

Ví dụ 4: Cho (4x² + 2x – 18)² – (4x² + 2x)² = m.(4x² + 2x – 9). Khi đó giá trị của m là:

Ta có (4x² + 2x – 18)² – (4x² + 2x)²

= (4x² + 2x – 18 + 4x² + 2x)(4x² + 2x – 18 – 4x² – 2x)

= (8x² + 4x – 18)(-18) = 2(4x² + 2x – 9)(-18)

= (-36)(4x² + 2x – 18) ⇒ m = -36

Ví dụ 5: Cho (x² + y² – 17)² – 4(xy – 4)² = (x + y + 5)(x – y + 3)(x + y + m)(x – y + n). Khi đó giá trị của m.n là

Ta có

(x² + y² – 17)² – 4(xy – 4)² = (x² + y² – 17)² – [2(xy – 4)]²

= (x² + y² – 17 + 2xy – 8)(x² + y² – 17 – 2xy + 8)

= (x² + y² + 2xy – 25)(x² + y² – 2xy – 9)

= [(x + y)² – 5²][(x – y)² – 3²]

= (x + y + 5)(x + y – 5)(x – y + 3)(x – y – 3)

Suy ra m = -5; n = -3 ⇒ m.n = (-5).(-3) = 15

Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình