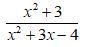Bất đẳng thức bunhiacopxki là gì? Công thức tính bunhiacopxki kèm bài tập từ cơ bản đến nâng cao

Bất đẳng thức Bunhiacopxki là gì ? Bất đẳng thức Bunhiacopxki có những công thức gì, hệ quả gì và cách chứng minh từng hệ quả ra sao cùng các dạng bài toán thường găp là những phần kiến thức quan trọng, chúng tôi sẽ giải đáp qua bài viết sau đây. Bạn tìm hiểu nhé !

Tham khảo thêm:

• Đối xứng tâm là gì? Các dạng bài tập thường gặp chi tiết từ A – Z
• Lý thuyết, cách chứng minh hai đường thẳng song song và bài tập có lời giải chia tiết 100%
• Định nghĩa, tính chất và công thức tính hình lập phương kèm VD minh họa

Bất đẳng thức bunhiacopxki là gì?

Bất đẳng thức Bunhiacopxki có tên gọi chính xác là bất đẳng thức Cauchy – Bunhiacopxki – Schwarz, do ba nhà toán học độc lập phát hiện và đề xuất, có nhiều ứng dụng trong các lĩnh vực toán học. Thường được gọi theo tên nhà Toán học người Nga Bunhiacopxki.

Bất đẳng thức này rất quen thuộc và thường được ứng dụng rất nhiều trong các bài toán về bất đẳng thức và cực trị.

Công thức của bất đẳng thức Bunhiacopxki

+ Bất đẳng thức Bunhiacopxki dạng cơ bản:

Dấu “=” xảy ra khi và chỉ khi a/c = b/d

+ Bất đẳng thức Bunhiacopxki cho 2 bộ số:

Với hai bộ số (a1, a2,….., an) và ( b1, b2,….,bn) ta có:

Dấu “=” xảy ra khi và chỉ khi a1/b1 = a2/b2 = ….an/bn

Với quy ước nếu một số nào đó (i = 1, 2, 3, …, n) bằng 0 thì tương ứng bằng 0

Chứng minh bất đẳng thức Bunhiacopxki

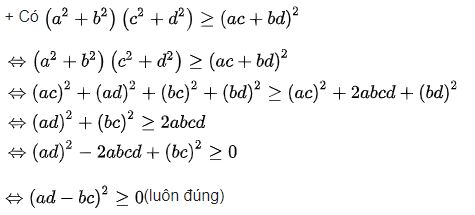
Hệ quả của bất đẳng thức Bunhiacopxki

Hệ quả 1:

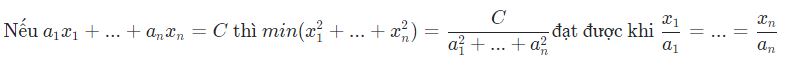
Hệ quả 2

Các dạng phát biểu của bất đẳng thức Bunhiacopxki

Bất đẳng thức Bunhiacopxki bao gồm các dạng sau đây:

Dạng cơ bản:

Dạng phân thức:

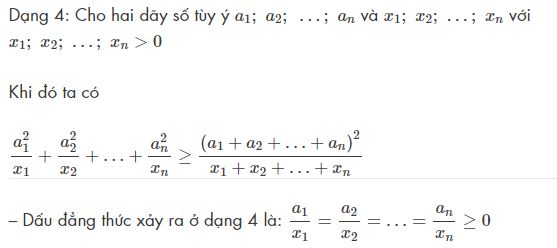
Trong các dạng trên thì bất đẳng thức dạng 1, dạng 2, dạng 3 gọi là các bất đẳng thức Bunhiacopxki dạng cơ bản và bất đẳng thức dạng 4 còn được gọi là bất đẳng thức Bunhiacopxki dạng phân thức.

Một số dạng đặc biệt

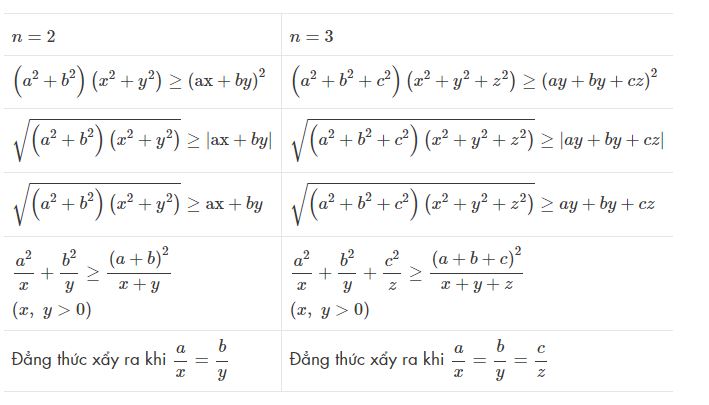
Các dạng bài tập bất đẳng thức bunhiacopxki thường gặp

Bài 1: Cho a, b, c là các số thực dương bất kỳ. Chứng minh rằng:

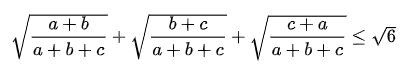
Lời giải:

Áp dụng bất đẳng thức Bunhiacopxki ta có:

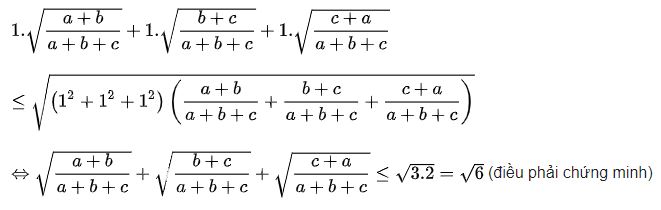
Dấu “=” xảy ra khi và chỉ khi a = b = c

Bài 2: Tìm giá trị lớn nhất của biểu thức:

Lời giải:

Điều kiện:  2 ≤ x ≤ 4

Áp dụng bất đẳng thức Bunhiacopxki có:

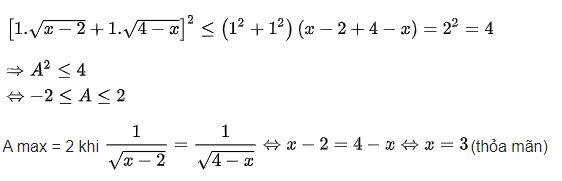
Vậy max A = 2 khi và chỉ khi x = 3

Bài 3: Chứng minh rằng nếu a, b, c là độ dài ba cạnh của một tam giác có p là nửa chu vi thì

Giải:

Áp dụng bất đẳng thức Bunhiacopxki có:

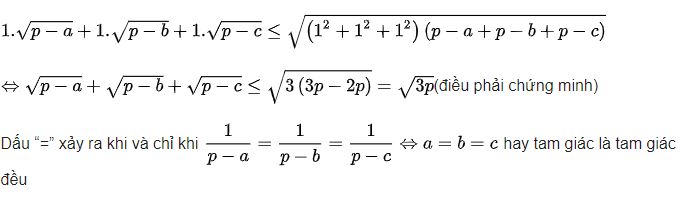
Bài 4: Cho các số a, b, c là các số thực dương tùy ý. Chứng minh rằng:

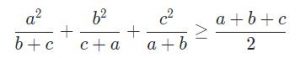
Giải:

Áp dụng bất đẳng thức bunhiacopxki.

Ta được:

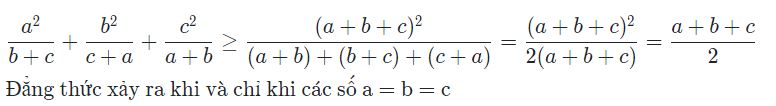
Bài 5: Cho a, b, là các số thực dương thỏa mãn . Tìm giá trị nhỏ nhất của biểu thức:

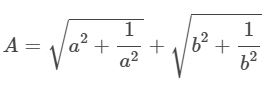
Giải:

Áp dụng bất đẳng thức Bunhiacopxki ta có:

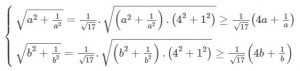
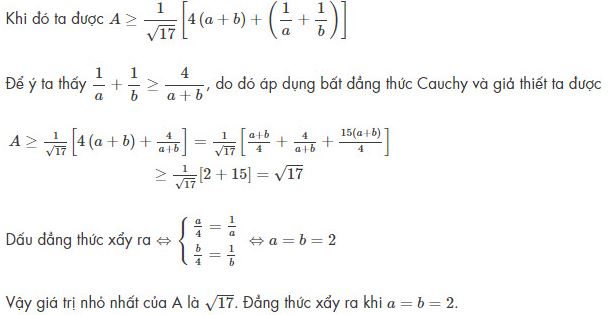
Trên đây là những kiến thức cơ bản về bất đẳng thức Bunhiacopxki. Cũng như là những kỹ thuật cơ bản mà hay dùng các bạn cần phải nắm rõ trong quá trình làm toán. Hy vọng những kiến thức tôi chia sẻ, sẽ giúp ích cho bạn trong quá trình học tập. Chúc các bạn luôn học tập và hoàn thành thật tốt trong các kì thi!