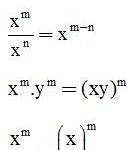Chia đơn thức với đơn thức là gì? Quy tắc chia đơn thức với đơn thức và bài tập có lời giải chính xác 100%

Các em đã biết cách nhân đơn thức với đơn thức, cách nhân đơn thức với đa thức, giờ ta có thể thực hiện phép chia đơn thức cho đơn thức hay không? Nếu được thì cách chia đơn thức cho đơn thức thực hiện như thế nào? Quy tắc chia đơn thức cho đơn thức ra sao, phát biểu như thế nào? cho ví dụ chia đơn thức với đơn thức và bài tập vận dụng? chúng ta hãy tìm hiểu qua bài viết dưới đây.

Tham khảo thêm:

• Công Thức Đạo Hàm Log, căn bậc 3 , căn u, căn x, căn logarit
• Công thức tính Chu Vi Hình Chữ Nhật và bài tập có lời giải từ A – Z
• Công thức tính diện tích tam giác vuông, cân, đều chính xác

Đơn thức chia hết cho đơn thức

Với A và B là hai đơn thức, B ≠ 0. Ta nói A chia hết cho B nếu tìm được một đơn thức Q sao cho A = B . Q

Kí hiệu: Q = A : B = A/B

Trong đó:

• A được gọi là đơn thức bị chia
• B được gọi là đơn thức chia
• Q được gọi là thương.

Quy tắc chia đơn thức cho đơn thức

Muốn chia đơn thức A cho đơn thức B (trường hợp A chia hết cho B) ta làm như sau:

• Chia hệ số của đơn thức A cho hệ số của đơn thức B.
• Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
• Nhân các kết quả vừa tìm được với nhau.

Nhắc lại một số quy tắc về lũy thừa:

Với mọi x, y ≠ 0; m, n ∈ N, m ≥ n thì:

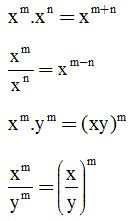
Một số dạng toán về chia đơn thức với đơn thức cơ bản

Dạng 1: Thực hiện phép tính và rút gọn biểu thức

Phương pháp: Sử dụng quy tắc chia đơn thức cho đơn thức để thực hiện phép tính và rút gọn biểu thức.

Ví dụ 1: Thực hiện phép tính:

a, Ta có: ( – 2 )⁵🙁 – 2 )³ = ( – 2 )⁵ – 3 = ( – 2 )² = 4.

b, Ta có: (3/4)⁵: (3/4)³= (3/4)^5-3=(3/4)²= 9/16

c, Ta có: (-12)³ : 8³ = -12³ : 8³= (-4 . 3)³ : (4 . 2)³ = ((-4.3)/4.2)³= (-3/2)³ = – 27/8

d, Ta có: 5³ : (-5)² = 5³ : 5² = 5^{3 – 2} = 5

Ví du 2: Thực hiện phép tính:

a,Ta có: ( xy² )⁴🙁 xy² )² = x⁴y⁸😡²y⁴ = x⁴ – 2.y⁸ – 4 = x²y⁴.

b, Ta có: x¹⁰ : (-x)⁸ = x¹⁰ : x⁸ = x¹⁰ – 8 = x²

c) Ta có: (-y)⁵ : (-y)⁴ = (-y)⁵ – 4 = -y

d Ta có: (-x)⁵ : (-x)³= (-x)⁵ – 3 = (-x)² = x²

Ví dụ 3: Thực hiện phép tính:

a, Ta có: 18x²y²z : 6xyz = (18 : 6)(x² : x)(y² : y)(z : z) = 3xy

b, Ta có: 5a³b : (-2a²b) = 5 : (-2)(a³ : a2)(b : b) = – 5/2 a

c, Ta có: 27x⁴y²z : 9x⁴y = (27 : 9)(x⁴ : x⁴)(y² : y).z = 3yz

Dạng 2: Tìm điều kiện để biểu thức A chia hết cho biểu thức B

Phương pháp: Sử dụng lý thuyết về điều kiện về số mũ của các biến để đơn thức A chia hết cho đơn thức B.

Ví dụ 1: Tìm điều kiện của n để biểu thức A chia hết cho biểu thức B trong các trường hợp sau:

A = 14x⁸yⁿ và B = -7x⁷y⁴

Ta có A : B = ( 14 – 7 ).( x⁸ : x⁷ ).( yⁿ : y⁴ )

= -2.x.y^n-4

Để A chia hết cho B thì:

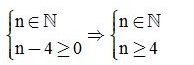
Ví dự 2: Tìm số tự nhiên n để mỗi phép chia sau là phép chia hết:

a, Ta có: x⁴ : xⁿ = x^4-n là phép chia hết nên 4 – n ≥ 0 ⇒ 0 ≤ n ≤ 4

suy ra: n ∈ {0; 1; 2; 3; 4}

b, Ta có: xⁿ : x³ = x^{n- 3} là phép chia hết nên n – 3 ≥ 0 ⇒ n ≥ 3

5xny3 : 4x³y² = 54 (xⁿ : x²)(y³ : y²) = 54 x^n-2 là phép chia hết

Suy ra: n – 2 ≥ 0 ⇒ n ≥ 2

c, Ta có: xⁿy^{n + 1} : x²y⁵ = (xⁿ : x²)(yⁿ⁺¹ : y⁵) = x^n-2.y^n-4 là phép chia hết

suy ra: n – 4 ≥ 0 ⇒ n ≥ 4

Ví dụ 3: Tính giá trị của biểu thức 15x⁴y³z² : 5xy²z² với x = 2, y = -10, z = 2004

Ta có: 15x⁴y³z² : 5xy²z² với x = 2, y = -10, z = 200

Ta có 15x⁴y³z² : 5xy²z² = 3 . x⁴ – 1 . y³ – 2 . z² – 2 = 3x³y

Tại x = 2, y = -10, z = 2004

Ta được: 3 . 2³(-10) = 3 . 8 . (-10) = -240.

Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình