Lý thuyết, cách chứng minh hai đường thẳng song song kèm VD

Hai đường thẳng song song là hai đường thẳng không có điểm chung. Vậy hôm nay chúng ta cùng nhau tìm hiểu về hai đường thẳng song song nhé! Bài giảng được chúng biên soạn theo chương trình sách giáo khoa của bộ giáo dục vơi nội dung chọn lọc, chi tiết sẽ giúp các em hiểu bài và nắm vững kiến thức bài học.

Tham khảo thêm:

• Cách chứng minh hai đường thẳng vuông góc và bài tập có lời giải chia tiết 100%
• Định nghĩa diện tích, thể tích của chóp tứ giác đều kèm bài tập có lời giải
• Định nghĩa hình chóp cụt là gì? Công thức tính diện tích, thể tích hình chóp cụt kèm ví dụ có lời giải

Hai đường thẳng song song là gì?

Hai đường thẳng song song (trong mặt phẳng) là hai đường thẳng không có điểm chung

Tính chất : Nếu một đường thẳng cắt hai đường thẳng song song thì

• Hai góc so le trong bằng nhau
• Hai góc đồng vị bằng nhau
• Hai góc trong cùng phía bù nhau

Ơ-clít về hai đường thẳng song song

Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song song với đường thẳng đó.

Dấu hiệu nhận biết hai đường thẳng song song:

+) Dấu hiệu 1: Dựa vào khái niệm hai đường thẳng song song.

+) Dấu hiệu 2: Dựa vào một đường thẳng cắt hai đường thẳng cần xét.

Nếu một đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì a và b song song với nhau.

+) Dấu hiệu 3: Dựa vào quan hệ từ vuông góc đến song song

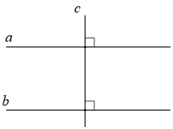
Cho đường thẳng a vuông góc với c, đường thẳng b vuông góc với c (a, b phân biệt) thì đường thẳng a song song với đường thẳng b (Hình vẽ trên)

Ta có công thức:

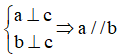
Dấu hiệu 4: Dựa vào tính cùng song song

Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau

Các dạng toán liên quan đến hai đường thẳng song song

Bài 1: Trên hình bên có ∠ABC = ∠A + ∠C. Hai đường thẳng Ax và Cy có song song với nhau hay không?

Giải:

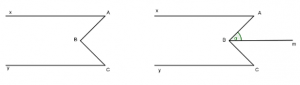
Vẽ tia Bm sao cho ∠ABm và ∠A là hai góc so le trong và bằng nhau.

Ta có: ∠ABm = ∠A ⇒ Ax // Bm    (1)

Tia Bm nằm giữa hai tia BA và BC nên ∠ABC = ∠ABm + ∠CBm hay ∠ABC = ∠A + ∠CBm

Mặt khác ∠ABC = ∠A + ∠C (gt) ⇒ ∠C = ∠CBm

Hai góc C và CBm bằng nhau ở vị trí so le trong nên Cy // Bm    (2)

Từ (1), (2) ⇒ Ax // Cy

Vậy Ax song song với Cy

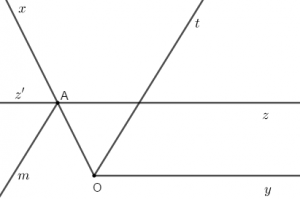
Bài 2: Cho góc ∠xOy = 145°. Trên tia Ox lấy điểm A. Qua A vẽ tia Az sao cho tia Az và Oy nằm trên cùng một nửa mặt phẳng bờ chứa tia Ox và ∠OAz = 35°

a) Chứng minh Az // Oy

b) Vẽ tia Az’ đối với tia Az. Chứng minh hai đường phân giác của góc xOy và OAz’ song song với nhau

Giải:

Bài 3; Cho tam giác ABC và một điểm M nằm trên cạnh BC. Khi điểm M di chuyển trên BC thì trung điểm I của AM di chuyển trên đường nào.

Giải:

Gọi E, F là trung điểm của AB và AC. Ta sẽ chứng minh E, I, F thẳng hàng.

Do E, I lần lượt là trung điểm của AB và AM nên EI là đường trung bình của tam giác ABM

=> EI //BM EI // BC (1)

Do F, I lần lượt là trung điểm của AC và AM nên IF là đường trung bình của tam giác AMC

=> IF // MC FI // BC (2)

Từ (1) và (2) => E, I, F thẳng hàng

Mà E là trung điểm AB, F là trung điểm AC nên EF là đường trung bình của tam giác ABC

Mà E, F cố định do AB, AC cố định

Nên khi M di chuyển trên BC thì trung điểm I của AM di chuyển trên EF là đường trung bình của tam giác ABC.

Bài 4: Cho tam giác ABC nhọn, các đường cao BD, CE. Gọi H, K lần lượt là các chân đường cao kẻ từ B và C đến DE. Chứng minh: HE = DK

Giải:

Vì BD, CF là đường cao của tam giác ABC nên

Do đó BDC vuông tại D, ΔCEB vuông tại E.

Gọi M là trung điểm của BC.

=> DM, EM là đường trung tuyến ứng với cạnh huyền ΔBDC và ΔCEB

Áp dụng tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông ta được:

Từ giả thuyết ta có tứ giác BHKC là hình thang vuông nên vẽ MIDE thì BH // MI //CK (1) (vì cùng vuông góc với đường thẳng DE).

Mà ta có: BM = MC (2) (do ta vẽ hình trên)

Từ (1), (2) => BH, MI, CK là ba đường thẳng song song và cách đều nên chúng chắn trên đường thẳng HK hai đoạn thẳng liên tiếp bằng nhau là HI = IK (3)

Áp dụng tính chất của đường cao ứng với cạnh đáy của tam giác cân MDE ta được MI là đường trung tuyến của tam giác MDE

=> I là trung điểm của ED

=> EI = ID (4)

Trừ theo vế đẳng thức (3) cho (4) ta được: HI EI = IK ID

HayHE = DK.

Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình