Lý thuyết và cách tính giới hạn của hàm số kèm bài tập có lời giải chính xác nhất

Giới hạn hàm số là kiến thức cơ bản lớp 11 những có rất nhiều bạn học sinh không nắm được giới hạn của hàm số hay giới han vô cực của hàm số,.. Chính vì vậy, trong bài viết dưới đây chúng tôi sẽ chia sẻ lý thuyết và bài tập về giới hạn hàm số các bạn cúng tham khảo nhé

Tham khảo thêm:

• Định nghĩa và hệ quả của định lý talet kèm bài tập có lời giải
• Lý thuyết phương trình tích và cách giải phương trình tích kèm bài tập từ A – Z
• Định nghĩa diện tích, thể tích của chóp tứ giác đều kèm bài tập có lời giải

Giới hạn hàm số là gì?

Giới hạn hàm số tại một điểm

Cho khoảng K chứa điểm x0 và hàm số y = f(x) xác định trên K hoặc trên K \ {x0}.

Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới x0 nếu với dãy số (xn) bất kì, xn ∈ K \{x0} và xn → x0, ta có f(xn) → L.

Kí hiệu:

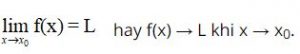
Nhận xét:

Giới hạn hữu hạn là gì?

Giới hạn một bên là gì?

Cho hàm số y = f(x) xác định trên (x0; b).

Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, x0 < xn < b và xn → x0, ta có f(xn) → L.

Kí hiệu:

Cho hàm số y = f(x) xác định trên (a; x₀).

Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi x → x₀ nếu với dãy số (x_n) bất kì, a < x_n < x₀ và x_n → x₀, ta có f(x_n) → L.

Kí hiệu:

Giới hạn hữu hạn của một hàm số tại vô cực

1, Cho hàm số y = f(x) xác định trên (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là số L khi x → +∞ nếu với dãy số (x_n) bất kì, x_n > a và x_n → +∞, ta có f(x_n) → L.

Kí hiệu:

2, Cho hàm số y = f(x) xác định trên (–∞; a).

Ta nói hàm số y = f(x) có giới hạn là số L khi x → –∞ nếu với dãy số (x_n) bất kì, x_n < a và x_n → –∞, ta có f(x_n) → L.

Kí hiệu:

Chú ý:

a) Với c, k là hằng số và k nguyên dương, ta luôn có:

b) Định lí 1 về giới hạn hữu hạn của hàm số khi x → x₀ vẫn còn đúng khi x_n → +∞ hoặc x → –∞

Giới hạn vô cực của hàm số là gì?

Giới hạn vô cực

Cho hàm số y = f(x) xác định trên (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là –∞ khi x → +∞ nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → –∞

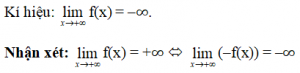
Một vài giới hạn đặc biệt

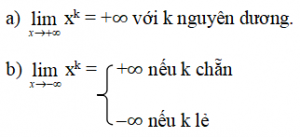
Quy tắc về giới hạn vô cực

a) Quy tắc tìm giới hạn của tích f(x).g(x)

b) Quy tắc tìm giới hạn của thương f(x)/ g(x)

Các dạng bài tập thường gặp trong giới hạn hàm số

Bài 1: Dùng định nghĩa tìm các giới hạn sau:

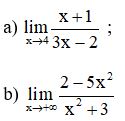
Lời giải:

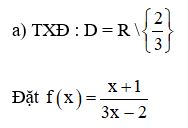
Lấy dãy (x_n) bất kì; x_n ∈ D; lim x_n = 4.

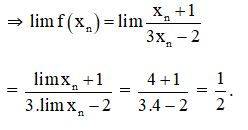
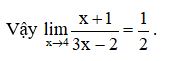
b) TXĐ: D = R.

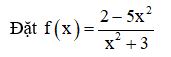
Lấy dãy (x_n) bất kì thỏa mãn x_n → +∞

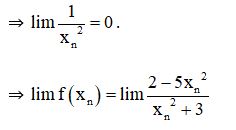
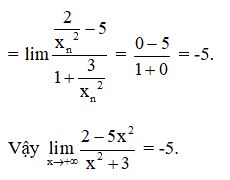
Bài 2: Tính các giới hạn sau:

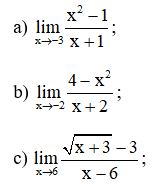
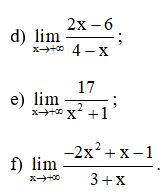
Lời giải:

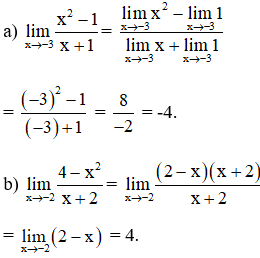
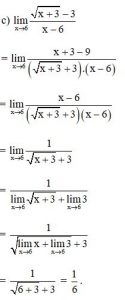
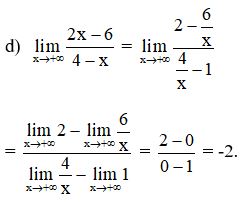
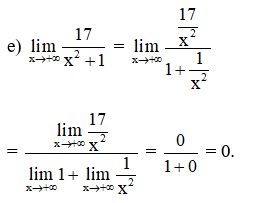
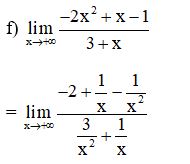
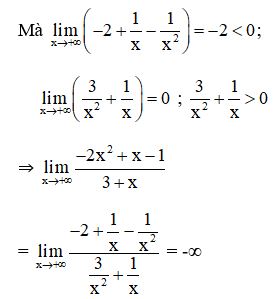
Bài 3: Tìm các giới hạn sau :

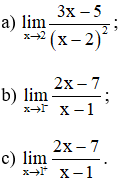
Lời giải:

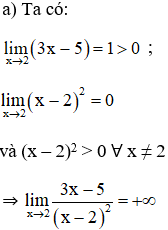
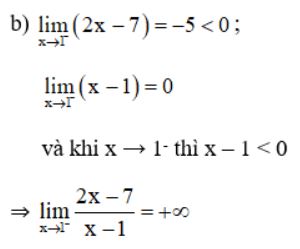
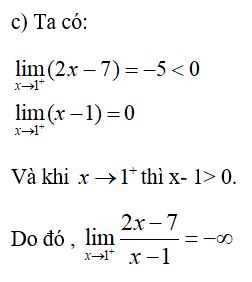
Bài 4: Xét tính liên tục của hàm số sau tại x = 3

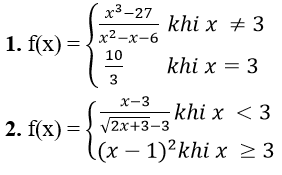
Giải:

1. Hàm số xác định trên R

Ta có f(3) = 10/3 và

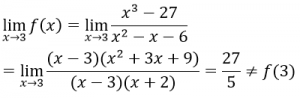
Vậy hàm số không liên tục tại x = 3

2. Ta có f(3) = 4 và

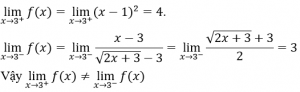
Vậy hàm số gián đoạn tại x = 3

Bài 5: Chọn giá trị f(0) để các hàm số sau liên tục tại điểm x = 0

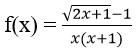
Bài 6: Tìm các giới hạn sau:

Giải;

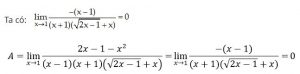
Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình