Cách tính diện tích xung quanh hình nón – Bí quyết tính toán diện tích xung quanh hình nón

Bài viết này nhắc lại kiến thức về hình nón, công thức và cách tính diện tích xung quanh của hình nón. Hình nón được tạo bởi một đáy hình tròn và một đường sinh. Công thức tính diện tích xung quanh hình nón là Sxq = πrl, trong đó π là 3.14159265359, r là bán kính mặt đáy của hình nón và l là độ dài đường sinh. Để tính diện tích xung quanh hình nón, ta cần biết bán kính và đường sinh của nó. Ví dụ: Cho hình nón có góc ở đỉnh là 120∘, độ dài đường sinh là 20 cm. Bằng cách áp dụng công thức Sxq = πrl, ta có diện tích xung quanh của hình nón là 200√3π (cm2).

1. Công thức tính diện tích xung quanh hình nón là gì?

Công thức tính diện tích xung quanh của hình nón là Sxq = πrl, trong đó:

• Sxq là diện tích xung quanh của hình nón
• π là số pi (3.14159265359)
• r là bán kính mặt đáy của hình nón
• l là độ dài đường sinh của hình nón

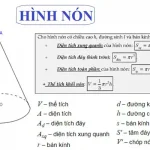
2. Hình nón được tạo thành từ những yếu tố nào?

Hình nón được tạo thành từ các yếu tố sau:

• Một cạnh tạo ra đáy của hình nón, và đây là một đường tròn có bán kính r.
• Một cạnh khác gọi là đỉnh, được kết nối từ trung điểm của cạnh tạo ra đáy tới một điểm ở phía trên.
• Một cạnh khác quét lên mặt xung quanh của hình nón và được gọi là đường sinh.

3. Làm thế nào để tính bán kính mặt đáy và độ dài đường sinh của hình nón?

Để tính bán kính mặt đáy của hình nón, chúng ta có thể sử dụng công thức r = C/(2π), trong đó C là chu vi của đáy.

Để tính độ dài đường sinh của hình nón, chúng ta có thể sử dụng công thức l = √(h^2 + r^2), trong đó h là chiều cao của hình nón.

Ví dụ:

Cho một hình nón có bán kính mặt đáy là 5 cm và chiều cao là 10 cm. Chúng ta có thể tính được:

• Bán kính mặt đáy: r = 5/2π ≈ 0.79 cm
• Độ dài đường sinh: l = √(10^2 + (5/2π)^2) ≈ 10.24 cm

4. Mô tả các bước để tính diện tích xung quanh của hình nón.

Bước 1: Xác định bán kính mặt đáy của hình nón.

Đầu tiên, cần xác định bán kính mặt đáy của hình nón. Bán kính được đo từ tâm O đến điểm trên cạnh đường tròn. Nếu không biết bán kính, có thể sử dụng công thức r = Đường kính / 2.

Bước 2: Xác định độ dài đường sinh của hình nón.

Tiếp theo, cần xác định độ dài đường sinh của hình nón. Đường sinh là khoảng cách từ điểm trên cạnh AB lên tới điểm A trên mặt xung quanh của hình nón.

Bước 3: Áp dụng công thức Sxq=πrl để tính diện tích xung quanh.

Sau khi đã biết bán kính và độ dài đường sinh, ta áp dụng công thức Sxq=πrl để tính diện tích xung quanh của hình nón. Trong công thức này, π (pi) là một số không gian có giá trị xấp xỉ là 3.14159265359.

5. Đưa ra ví dụ cụ thể về cách tính diện tích xung quanh hình nón.

Ví dụ:

Giả sử chúng ta có một hình nón với bán kính đáy là 5 cm và độ dài đường sinh là 10 cm. Để tính diện tích xung quanh của hình nón, ta áp dụng công thức Sxq=πrl.
Sxq = π * 5 * 10
= 50π (cm²)
Vậy diện tích xung quanh của hình nón trong trường hợp này là 50π (cm²).

6. Có thể sử dụng công thức này cho các loại hình nón khác nhau không?

Công thức Sxq=πrl có thể được sử dụng cho tất cả các loại hình nón, bất kể kích thước hay tỉ lệ giữa bán kính đáy và độ dài đường sinh.

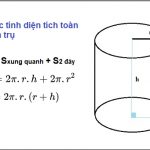
7. Ngoài diện tích xung quanh, còn có công thức và cách tính diện tích toàn phần của hình nón không?

Ngoài công thức để tính diện tích xung quanh của hình nón, có một công thức khác để tính diện tích toàn phần của hình nón. Diện tích toàn phần bao gồm cả diện tích xung quanh và diện tích đáy của hình nón. Công thức tính diện tích toàn phần là Sp = Sxq + Sđ
Sp: Diện tích toàn phần
Sxq: Diện tích xung quanh
Sđ: Diện tích đáy

8. Tại sao trong công thức lại có π (pi) và vì sao giá trị của pi là 3.14159265359?

Trong công thức Sxq=πrl, π (pi) là một hằng số không gian có giá trị xấp xỉ là 3.14159265359. Giá trị này đã được xác định từ hàng ngàn năm qua dựa vào quan hệ giữa chu vi và đường kính của một vòng tròn.

9. Đường cao của hình nón có ảnh hưởng đến diện tích xung quanh không? Vì sao?

Đường cao của hình nón không ảnh hưởng trực tiếp đến diện tích xung quanh của nó. Diện tích xung quanh chỉ phụ thuộc vào bán kính đáy và độ dài đường sinh.

10. Lợi ích và ứng dụng của việc biết công thức và cách tính diện tích xung quanh hình nón trong cuộc sống hàng ngày là gì?

Biết công thức và cách tính diện tích xung quanh hình nón có thể có những ứng dụng và lợi ích sau:
– Giúp trong việc tính toán và đo lường các đối tượng hình nón trong ngành xây dựng, kiến trúc.
– Hỗ trợ trong việc tính diện tích sàn hoặc bề mặt các vật thể hình nón như lon đồ uống, chiếc nón, v.v.
– Cung cấp kiến thức cơ bản về hình học không gian và tăng cường khả năng tư duy logic và trừu tượng của người học.

Tổng kết, diện tích xung quanh hình nón là tổng diện tích của bề mặt đáy và mặt cong của hình nón. Công thức tính diện tích xung quanh là S = πrL, trong đó r là bán kính đáy và L là dạng lưu của đường sinh góc của mặt cong. Việc tính toán diện tích xung quanh hình nón giúp ta hiểu rõ hơn về cấu trúc và tính chất của hình học này.