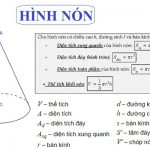
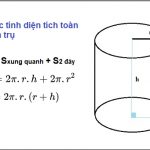
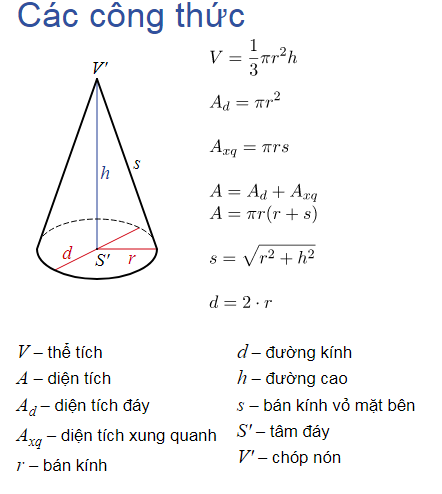
Các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích hình nón

Diện tích toàn phần hình nón là một trong những khái niệm cơ bản trong toán học. Để tính diện tích toàn phần của hình nón, ta cộng thêm diện tích xung quanh hình nón và diện tích mặt đáy. Diện tích xung quanh hình nón được tính bằng công thức: Sxq = πr*l, trong đó r là bán kính đáy hình nón và l là đường sinh hình nón. Diện tích mặt đáy được tính bằng công thức: Sđ = πr^2. Thể tích của hình nón được tính bằng công thức: V = (1/3)Sđ*h, trong đó h là chiều cao của hình nón. Việc áp dụng các công thức này dễ dàng với việc thay các thông số vào để tính toán.

Nội Dung

Công thức tính diện tích toàn phần của hình nón là gì?

Diện tích toàn phần của hình nón được tính bằng công thức Stp = Sxq + Sd, trong đó:

Stp là diện tích toàn phần của hình nón.
Sxq là diện tích xung quanh của hình nón.
Sd là diện tích mặt đáy của hình nón.

Để tính diện tích xung quanh của hình nón, ta sử dụng công thức Sxq = π × r × l, trong đó:

Sxq là diện tích xung quanh của hình nón.
r là bán kính đáy của hình nón.
l là đường sinh của hình nón.

Đối với diện tích mặt đáy của hình nón, ta sử dụng công thức Sd = π × r^2, trong đó:

Sd là diện tích mặt đáy của hình nón.
r là bán kính đáy của hình nón.

Ví dụ:

Hãy tính diện tích toàn phần và diện tích mặt đáy của một chiếc cốc có dạng như một hình nón. Bán kính đáy của cốc là 5 cm và đường sinh của cốc là 10 cm.

Áp dụng công thức, ta có:

Diện tích xung quanh Sxq = π × 5 × 10 = 157.08 cm^2
Diện tích mặt đáy Sd = π × (5)^2 = 78.54 cm^2

Từ đó, ta có diện tích toàn phần Stp = Sxq + Sd = 157.08 + 78.54 = 235.62 cm^2.

2. Diện tích toàn phần hình nón được tính bằng cách nào?

Để tính diện tích toàn phần của một hình nón, ta cần biết diện tích xung quanh và diện tích mặt đáy của hình nón. Công thức để tính diện tích toàn phần là Stp = Sxq + Sđ.

Cách 1:

Có thể sử dụng công thức trực tiếp để tính diện tích toàn phần. Bước đầu tiên là tính diện tích xung quanh (Sxq), được định nghĩa là πrL, trong đó r là bán kính của đáy và L là chu vi xung quanh at mặt dạng tròn.

Sau đó, ta cần tính diện tích mặt đáy (Sđ), có công thức Sđ = πr², trong đó r là bán kính của đáy hình nón.

Thêm cả hai giá trị này lại với nhau sẽ cho ta diện tích toàn phần của hình nón.

Cách 2:

Một cách khác để tính diện tích toàn phần của hình nón là thông qua các thông số khác như bán kính, chiều cao và góc sóc. Đầu tiên, ta tính diện tích mặt bên của hình nón theo công thức Smb = (1/2) * π * r * l, trong đó r là bán kính đáy và l là đường nhảy từ đỉnh xuống mặt đáy. Sau đó, ta cần tính diện tích mặt dưới (Sd) và diện tích mặt trên (St) của hình nón theo công thức Sđ = πr² và St = πR², trong đó R là bán kính của thành phần móc ở đỉnh và tạo gốc tròn với diện tích xung quanh fthành phần móc.

Tổng cộng các giá trị này lại sẽ cho ta diện tích toàn phần của hình nón.

Cách 3:

Thêm vào hai cách trên, chúng ta cũng có thể sử dụng thông qua công thức tổng quát: Stp = Sxq + Smb, trong đó Sxq là diện tích xung quanh và Smb là diện tích mặt bên của hình nón.

3. Trong công thức tính diện tích toàn phần hình nón, các thông số cần biết là gì?

Để áp dụng công thức và tính toán được diện tích toàn phần của hình nón, ta cần biết các thông số sau:

– Bán kính đáy (r):

Đây là khoảng cách từ tâm của đáy hình nón tới bất kỳ điểm nào trên đường biên của đáy.
Đơn vị đo của bán kính thường là mét (m) hoặc centimet (cm).

– Đường cao (h):

Là khoảng cách từ đỉnh của hình nón xuống mặt phẳng chứa đáy.
Đơn vị đo của đường cao thường là mét (m) hoặc centimet (cm).

– Đường sinh (L):

Là chu vi xung quanh cho phần cạnh góc vuông là gốc tròn và được tính bằng công thức L = 2πr.
Đơn vị đo của chu vi xung quanh thường là mét (m) hoặc centimet (cm).

Các thông số này sẽ giúp chúng ta tính toán diện tích xung quanh và diện tích mặt đáy, từ đó tính được diện tích toàn phần của hình nón.

4. Làm sao để tính diện tích mặt đáy của hình nón?

Để tính diện tích mặt đáy của hình nón, chúng ta cần biết bán kính của đáy. Diện tích mặt đáy được tính bằng công thức:

Công thức:

– Đối với hình tròn: S = πr²
– Đối với hình vuông: S = a²
– Đối với hình chữ nhật: S = ab
Trong đó, S là diện tích mặt đáy, r là bán kính của đáy (đối với hình tròn), a và b là các cạnh của đáy (đối với hình vuông và hình chữ nhật).

Ví dụ, nếu ta có một hình nón có bán kính đáy là 5cm (hình tròn), để tính diện tích mặt đáy, ta sử dụng công thức S = πr². Thay vào giá trị r=5cm trong công thức, ta có:
S = 3.14 x 5² ≈ 78.5 cm².
Do đó, diện tích mặt đáy của hình nón này là khoảng 78.5 cm².

5. Đường cao của hình nón có ảnh hưởng đến diện tích toàn phần không? Vì sao?

Đường cao của hình nón có ảnh hưởng đến diện tích toàn phần. Diện tích toàn phần của hình nón bao gồm diện tích xung quanh và diện tích mặt đáy. Đường cao là một thành phần quan trọng trong việc tính diện tích xung quanh và diện tích toàn phần của hình nón.

Khi đường cao thay đổi, diện tích xung quanh và diện tích mặt đáy của hình nón cũng sẽ thay đổi theo. Điều này xuất phát từ công thức tính diện tích toàn phần của hình nón, trong đó công thức cho biết rằng diện tích toàn phần bằng diện tích xung quanh (Sxq) cộng với diện tích mặt đáy (Sđ). Vì vậy, khi đường cao tăng lên, diện tích xung quanh và diện tích mặt đáy cũng tăng theo và ngược lại.

6. Bán kính đáy của hình nón có tác động lên diện tích xung quanh không? Tại sao?

Bán kính đáy của hình nón có tác động lên diện tích xung quanh. Diện tích xung quanh của hình nón được tính bằng công thức Sxq = πrL, trong đó r là bán kính đáy và L là đường sinh hình nón.

Khi bán kính đáy tăng lên, diện tích xung quanh của hình nón cũng tăng theo. Điều này có thể hiểu được từ công thức tính diện tích xung quanh, trong đó diện tích xung quanh tỉ lệ thuận với bán kính. Khi bán kính càng lớn, diện tích xung quanh cũng càng lớn.

Đây chính là lí do tại sao bán kính đáy của hình nón (hay các loại hình khác) có tác động lên diện tích xung quanh. Thay đổi giá trị của bán kính sẽ thay đổi diện tích xung quanh và ngược lại.

7. Có thể áp dụng công thức tính diện tích xung quanh và công thức tính diện tích toàn phần cho các loại hình nón khác nhau không? Vì sao?

Công thức tính diện tích xung quanh và công thức tính diện tích toàn phần có thể được áp dụng cho tất cả các loại hình nón, bao gồm cả hình nón vuông và hình nón không vuông. Điều này là do cách tính diện tích xung quanh và diện tích mặt đáy trong các công thức này không phụ thuộc vào hình dạng của đáy hay cạnh của hình nón. Thay vào đó, chúng chỉ liên quan đến bán kính của đáy và chiều cao của hình nón.

Ví dụ, để tính diện tích xung quanh một hình nón, chúng ta sử dụng công thức Sxq = πrℓ (trong đó r là bán kính đáy và ℓ là đường sinh). Bản chất của công thức này vẫn giữ nguyên bất kể hình dạng của đáy hay chiều cao của hình nón.

Tương tự, để tính diện tích toàn phần của một hình nón, chúng ta sử dụng công thức Stp = Sxq + Sd (trong đó Sd là diện tích mặt đáy). Công thức này cũng không bị ảnh hưởng bởi hình dạng hay cạnh của đáy.

8. Tại sao chúng ta sử dụng Pi trong công thức tính diện tích xung quanh của hình nón?

Ý nghĩa của Pi trong công thức

Công thức tính diện tích xung quanh của hình nón bao gồm việc nhân Pi với bán kính đáy và đường sinh. Pi (π) là một số vô tỉ, gần đúng bằng 3.14, đã được sử dụng trong toán học từ ngàn năm trước. Pi là tỷ lệ giữa chu vi của một vòng tròn và đường kính của nó. Trong trường hợp này, khi áp dụng vào công thức tính diện tích xung quanh của hình nón, ta sử dụng Pi để tính toán tỷ lệ giữa chu vi đáy và chiều cao hình nón.

– Ví dụ: Nếu bán kính đáy và chiều cao là các số nguyên, diện tích xung quanh có thể được biểu diễn bằng công thức A = πrL, trong đó r là bán kính và L là đường sinh.
– Vì Pi là một số không chãn và vô tỉ, công thức này cung cấp kết quả chính xác cho diện tích xung quanh của hình nón.

Ứng dụng của Pi trong toán học

Pi không chỉ được sử dụng trong công thức tính diện tích xung quanh của hình nón, mà còn xuất hiện trong các công thức khác như tính chu vi và diện tích của hình tròn, tính thể tích của hình cầu và nhiều ứng dụng khác trong toán học và các lĩnh vực liên quan. Vì Pi là một số phi tự nhiên, nó có giá trị xấp xỉ được sử dụng để giải quyết các bài toán thực tế và tạo ra các công thức tiện ích cho chúng ta.

– Ví dụ: Trong vật lý, Pi cũng được sử dụng để tính diện tích bề mặt của các đối tượng tròn như ống dẫn hoặc vỏ bình xăng.
– Sự hiểu biết về Pi là rất quan trọng trong toán học và các lĩnh vực khoa học khác, giúp chúng ta áp dụng công thức một cách chính xác và có ý nghĩa.

9. Diện tích xung quanh và diện tích mặt đáy cùng tồn tại trong công thức tính diện tích toàn phần vì lí do gì?

Khi tính diện tích toàn phần của hình nón, ta phải tính tổng diện tích xung quanh và diện tích mặt đáy. Tại sao chúng lại cùng tồn tại trong công thức này?

1. Lý do liên quan đến cấu trúc hình nón:

Hình nón được tạo ra khi quay một tam giác vuông một vòng quanh cạnh góc vuông cố định.
Diện tích xung quanh là diện tích toàn bộ bề mặt của hình nón, bao gồm từ đỉnh xuống đáy.
Diện tích mặt đáy là diện tích của một hình tròn có bán kính là bán kính đáy của hình nón.

Vì vậy, để tính tổng diện tích toàn phần, ta phải bao gồm cả diện tích xung quanh và diện tích mặt đáy.

2. Lý do liên quan đến khối lượng và dung tích:

Nếu chỉ xét diện tích xung quanh, chúng ta chỉ tính toán phần bề mặt của hình nón.
Nếu chỉ xét diện tích mặt đáy, chúng ta chỉ tính toán phần không gian bên trong của hình nón.
Việc tính cả diện tích xung quanh và diện tích mặt đáy cho phép chúng ta đo lường cả khối lượng và dung tích của hình nón, giúp hiểu rõ hơn về các thuộc tính không gian của nó.

Vì vậy, công thức tính diện tích toàn phần của hình nón bao gồm cả diện tích xung quanh và diện tích mặt đáy để đảm bảo rằng ta có thể hiểu được và đo lường được cả khối lượng và dung tích của hình nón.

10. Giải thích ý nghĩa của công thức để tính thể tích hình nón và cách áp dụng vào các bài tập cụ thể trong toán học.

Công thức để tính thể tích hình nón là một công thức quan trọng trong toán học, với ý nghĩa quan trọng trong việc giải quyết các bài tập liên quan đến không gian và hình học.

1. Ý nghĩa của công thức tính thể tích:

Công thức để tính thể tích hình nón là: Thể tích = 1/3 × diện tích mặt đáy × chiều cao

Thể tích là một khái niệm quan trọng trong việc đo lường và xác định khối lượng của một vật thể.
Công thức này cho phép chúng ta tính được thể tích của hình nón, dựa trên diện tích mặt đáy và chiều cao của nó.
Việc biết được thể tích giúp chúng ta hiểu rõ hơn về không gian và các thuộc tính liên quan của hình nón.

2. Áp dụng vào các bài tập cụ thể:

Công thức để tính thể tích hình nón có thể được áp dụng vào các bài tập cụ thể trong toán học. Ví dụ:

Bài tập yêu cầu tính toán dung tích một bồn nước có hình dạng là một nón.
Bài tập yêu cầu xác định chiều cao của một nón khi chỉ biết diện tích mặt đáy và thể tích.
Bài tập yêu cầu xác định diện tích mặt đáy của một nón khi chỉ biết thể tích và chiều cao.

Công thức tính thể tích hình nón giúp chúng ta giải quyết các bài toán liên quan đến không gian và hình học, là công cụ quan trọng trong việc áp dụng kiến thức toán học vào thực tế và giải quyết các vấn đề thực tế.

Tổng kết lại, diện tích toàn phần của hình nón là tổng diện tích của mặt nón và mặt đáy. Công thức tính diện tích toàn phần được dùng là S = πrl + πr^2, trong đó r là bán kính đáy, l là cạnh xung quanh hình nón. Việc tính toán diện tích toàn phần giúp chúng ta hiểu rõ hơn về cấu trúc và tính chất của hình nón.