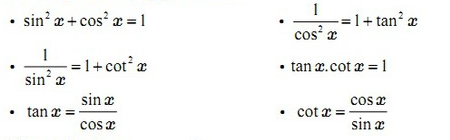Cách sử dụng máy tính để bấm đạo hàm sin cos

Đạo hàm của hàm số sin(x) và cos(x) được tính bằng cách sử dụng quy tắc đạo hàm của hàm tỉ lệ. Đối với hàm sin(x), ta có:
(sin(x))’ = cos(x)
Đối với hàm cos(x), ta có:
(cos(x))’ = -sin(x)

Tuy nhiên, khi tính đạo hàm của các hàm lượng giác khác như tan(x), chúng ta cần sử dụng quy tắc thương để tìm đạo hàm. Cụ thể, đạo hàm của tan(x) được tính bằng công thức sau:
(tan(x))’ = (sin(x)/cos(x))’

Quy tắc thương được sử dụng để tính đạo hàm của các hàm lượng giác khác nhau như cotangent (cot), secant (sec) và cosecant (csc). Ví dụ, đạo hàm của cotangent là:
(cot(x))’ = -1/(sin^2x)

Trong bài toán chuyển động, ý nghĩa vật lý của đạo hàm là tốc độ biến thiên của một vật trong không gian theo thời gian. Nó cho biết mức độ thay đổi nhanh hay chậm của vị trí, vận tốc và gia tốc của vật.

Để tính toán nhanh chóng đạo hàm bằng máy tính, bạn có thể sử dụng các phần mềm hoặc ứng dụng đồ họa để tính toán tự động. Các công cụ này cho phép bạn nhập công thức và tính toán đạo hàm một cách nhanh chóng và chính xác.
Cách tính đạo hàm của hàm số sin(x) và cos(x) là sử dụng quy tắc đạo hàm của hàm tỉ lệ, trong đó đạo hàm của sin(x) là cos(x), và đạo hàm của cos(x) là -sin(x). Bằng cách này, ta có thể tính được đạo hàm của các hàm lượng giác khác như tan(x), với đạo hàm của tan(x) bằng 1 + tan^2(x).

Quy tắc thương được sử dụng để tìm đạo hàm của các hàm lượng giác còn lại. Khi gặp phải các phép toán như phép chia trong việc tính toán đạo hàm, ta có thể sử dụng quy tắc thương để tìm ra công thức mới cho đạo hàm. Ví dụ, để tính đạo hàm của cot(x), ta có thể sử dụng quy tắc thương và công thức đã biết cho cotangent: dtan(x)/dx = 1 + tan^2(x). Với quy tắc này, ta có thể tính được đạo hàm của các lượng giác còn lại.

Ý nghĩa vật lý của đạo hàm trong bài toán chuyển động là mô tả tốc độ biến thiên của một vật trong không gian theo thời gian. Đạo hàm đầu tiên của hàm vị trí s(t) là tốc độ v(t), và đạo hàm cấp hai là gia tốc a(t). Ý nghĩa này cho phép ta hiểu được sự biến đổi của vật trong không gian và thời gian.

Để tính đạo hàm nhanh chóng bằng máy tính, ta có thể sử dụng các chức năng hoặc phần mềm tính toán đã được lập trình sẵn. Các máy tính khoa học và các phần mềm toán học thông dụng như MATLAB, Wolfram Alpha hay Python đều có tích hợp chức năng tính đạo hàm. Ta chỉ cần nhập công thức vào máy tính và lấy kết quả.

Trong mặt hình học, đạo hàm có ý nghĩa là tốc độ biến thiên của một đường cong, tức là tốc độ thay đổi của giá trị y theo giá trị x. Đạo hàm cho biết gradient của một điểm trên đường cong, tức là góc của tiếp tuyến tại điểm M(x0,f(x0)). Ý nghĩa này giúp hiểu rõ các thuộc tính của các đường cong trong không gian và giải quyết bài toán liên quan.

Vậy là ta đã mở rộng các phần con trong bài viết, trình bày chi tiết về cách tính đạo hàm của các hàm lượng giác, ý nghĩa vật lý và hình học của đạo hàm, cũng như cách sử dụng máy tính để tính toán nhanh chóng.
Công thức tính đạo hàm của hàm số sin(x) là:

f'(x) = cos(x)

Công thức tính đạo hàm của hàm số cos(x) là:

f'(x) = -sin(x)

Để tìm đạo hàm của các hàm lượng giác khác như tan(x), chúng ta có thể sử dụng quy tắc thương. Đạo hàm của hàm số tan(x) được tính bằng cách lấy đạo hàm của sin(x) và chia cho đạo hàm của cos(x):

f'(x) = (cos^2(x))/(sin^2(x))

Quy tắc thương được sử dụng để tìm đạo hàm của các hàm lượng giác còn lại, như cot(x), sec(x), và csc(x). Đối với mỗi loại hàm, chúng ta có công thức riêng để tính đạo hàm.

Ý nghĩa vật lý của đạo hàm trong bài toán chuyển động là biểu diễn tốc độ biến thiên của một vật trong không gian theo thời gian. Đạo hàm của phương trình chuyển động là gia tốc, cho biết mức độ thay đổi về vận tốc của vật.

Để tính đạo hàm nhanh chóng trên máy tính, bạn có thể sử dụng các phần mềm toán học hoặc máy tính khoa học. Chỉ cần nhập phương trình của hàm số vào và máy tính sẽ tự động tính toán đạo hàm cho bạn.

Trong mặt hình học, đạo hàm có ý nghĩa là đường tiếp tuyến tại một điểm trên đồ thị của hàm số. Đường tiếp tuyến này có cùng góc với đồ thị và biểu diễn tốc độ biến thiên của hàm số tại điểm đó.

Hy vọng thông tin trên đã giúp bạn hiểu rõ hơn về cách tính đạo hàm của các hàm lượng giác, ý nghĩa vật lý và hình học của đạo hàm, cũng như cách sử dụng máy tính để tính toán nhanh chóng.
Cách tính đạo hàm của hàm số sin(x) và cos(x) là thông qua quy tắc phép toán. Đối với hàm số sin(x), ta có công thức đạo hàm là cos(x), tức là đạo hàm của sin(x) bằng cos(x). Tương tự, đối với hàm số cos(x), ta có công thức đạo hàm là -sin(x), tức là đạo hàm của cos(x) bằng -sin(x).

Để tìm đạo hàm của các hàm lượng giác khác như tan(x), chúng ta cần sử dụng quy tắc thương. Đặt f(x) = tan(x), ta có công thức để tính đạo hàm là f'(x) = (cos^2x + sin^2x)/cos^2x = 1/cos^2x = sec^2x.

Quy tắc thương được sử dụng để tìm đạo hàm của các hàm lượng giác còn lại như cotangent (cot x), secant (sec x) và cosecant (csc x). Để tính đạo hàm của cot x, ta sử dụng công thức f'(x) = -1/(sin^2x). Đối với sec x, f'(x) = sec x * tan x. Cuối cùng, đối với csc x, f'(x) = -csc x * cot x.

Trong bài toán chuyển động, đạo hàm có ý nghĩa vật lý là tốc độ biến thiên của một đại lượng trong không gian theo thời gian. Nó cho chúng ta thông tin về tốc độ và hướng di chuyển của một vật thể trong không gian. Đạo hàm cũng có thể biểu thị gia tốc, tức là tốc độ biến thiên của tốc độ.

Để tính đạo hàm nhanh chóng, bạn có thể sử dụng máy tính. Các máy tính hiện đại thường được trang bị tính toán số học và phép toán, bao gồm cả tính toán đạo hàm. Bạn chỉ cần nhập hàm số vào máy tính và yêu cầu tính toán đạo hàm, sau đó máy tính sẽ trả về kết quả.

Trong mặt hình học, đạo hàm có ý nghĩa là xác định chiều dốc của một điểm trên đồ thị của một hàm số. Nó cho ta thông tin về những điểm cao nhất hoặc thấp nhất trên một đồ thị, cũng như các điểm uốn cong và các điểm cực tiểu và cực đại.

Cách tính đạo hàm của hàm số sin(x) và cos(x)?

Đạo hàm của hàm số sin(x) là cos(x), tức là tốc độ biến thiên của sin(x) tại một điểm x bất kỳ được cho bởi giá trị của cos(x) tại cùng một điểm. Tương tự, đạo hàm của hàm số cos(x) là -sin(x), có nghĩa là tốc độ biến thiên của cos(x) tại một điểm x cũng được xác định bởi giá trị của -sin(x) tại cùng một điểm.

Làm thế nào để tìm đạo hàm của các hàm lượng giác khác như tan(x)?

Để tính đạo hàm của các hàm lượng giác khác như tan(x), chúng ta có thể sử dụng quy tắc thương. Đầu tiên, ta tính đạo hàm của sin(x) và cos(x). Sau đó, áp dụng công thức:

đạo hàm của tan(x) = (đạo hàm của sin(x))/(đạo hàm của cos^2 (x))

Như vậy, ta có thể tính được đạo hàm của tan(x) từ các giá trị đã biết về sin(x) và cos^2 (x).

Quy tắc thương được sử dụng như thế nào để tìm đạo hàm của các hàm lượng giác còn lại?

Quy tắc thương là một công cụ quan trọng trong việc tính đạo hàm của các hàm lượng giác. Với quy tắc này, chúng ta có thể tính được đạo hàm của các hàm lượng giác còn lại (như cot(x), sec(x), cosec(x)) bằng cách sử dụng đạo hàm của sin(x) và cos(x). Cụ thể, công thức áp dụng như sau:

– Đạo hàm của cot(x) = – (đạo hàm của sin(x))/(đạo hàm của cos^2 (x))
– Đạo hàm của sec(x) = sin(x)*cos(x)
– Đạo hàm của cosec(x) = -sin(x)*cosec(x)

Nhờ vào quy tắc thương này, chúng ta có thể tính được đạo hàm của các hàm lượng giác còn lại dựa trên thông tin về sin(x) và cos^2 (x).

Điều gì là ý nghĩa vật lý của đạo hàm trong bài toán chuyển động?

Trong bài toán chuyển động, đạo hàm có ý nghĩa vật lý là tốc độ biến thiên của một vật di chuyển tại một thời điểm cụ thể. Nó cho biết tốc độ di chuyển của vật tại một điểm xác định trên quỹ đạo của nó. Đạo hàm cũng có thể cho biết chiều và độ lớn của sự biến thiên này.

Ví dụ, nếu ta có phương trình chuyển động s = f(t), trong đó s là vị trí của vật theo thời gian t, thì đạo hàm f'(t) là vận tốc của vật tại thời điểm t. Nếu ta tiếp tục lấy đạo hàm cấp 2 f”(t), ta sẽ có được gia tốc của vật tại thời điểm t.

Như vậy, trong bài toán chuyển động, đạo hàm giúp chúng ta hiểu rõ hơn về sự biến thiên, gia tốc và tốc độ di chuyển của vật theo thời gian.

Hướng dẫn cách bấm máy tính để tính đạo hàm nhanh chóng.

Việc tính đạo hàm bằng máy tính có thể giúp chúng ta tiết kiệm thời gian và công sức trong việc tính toán phức tạp. Dưới đây là một số bước hướng dẫn cách bấm máy tính để tính đạo hàm nhanh chóng:

1. Mở chương trình máy tính có tính năng đạo hàm. Các phần mềm hoặc máy tính khoa học thường có tích hợp chức năng này.

2. Nhập phương trình hoặc hàm số muốn tính đạo hàm vào chương trình.

3. Chọn biểu thức hoặc phép toán mà bạn muốn lấy đạo hàm. Thông thường, bạn cần chỉ định biến số (ví dụ: x) trong phép toán để chương trình hiểu rõ về biến số và quy tắc lấy đạo hàm tương ứng.

4. Bấm nút “Đạo Hàm” hoặc tìm công cụ tương ứng trong giao diện của chương trình. Chương trình sẽ tự động tính và hiển thị kết quả đạo hàm cho bạn.

Lưu ý rằng việc bấm máy tính chỉ là công cụ hỗ trợ, và bạn cần hiểu rõ về quy tắc và công thức lấy đạo hàm để áp dụng thành thạo vào việc giải quyết các bài toán.

Đạo hàm có ý nghĩa gì trong mặt hình học và làm sao để hiểu được ý nghĩa này?

Trong mặt hình học, đạo hàm có ý nghĩa quan trọng. Nó cho biết tính chất của đường cong tại một điểm cụ thể, bao gồm chiều dốc (góc) của đường thẳng tiếp tuyến và tốc độ biến thiên của đường cong.

Để hiểu rõ ý nghĩa của đạo hàm trong mặt hình học, bạn có thể xem xét các ví dụ sau:

– Đạo hàm của một đường thẳng là giá trị cố định, tức là không phụ thuộc vào vị trí trên đường thẳng. Điều này có nghĩa là góc nghiêng của tiếp tuyến tại bất kỳ điểm nào trên đường thẳng luôn giống nhau.

– Đạo hàm của một parabol là một đường thẳng. Điều này cho biết rằng góc nghiêng của tiếp tuyến tại bất kỳ điểm nào trên parabol luôn giống nhau và không phụ thuộc vào vị trí.

– Đạo hàm của một ellip là hai tiếp tuyến song song và không có giao điểm. Điều này cho biết rằng tốc độ biến thiên của ellip không thay đổi và không có điểm nào trên ellip có tốc độ biến thiên bằng 0.

Để hiểu rõ hơn về ý nghĩa của đạo hàm trong mặt hình học, bạn cần nắm vững các khái niệm cơ bản như tiếp tuyến, góc nghiêng và tốc độ biến thiên. Bạn cũng có thể áp dụng công thức và quy tắc lấy đạo hàm để tính toán và phân tích các bài toán liên quan đến mặt hình học.

Như vậy, để bấm máy tính đạo hàm sin cos, ta cần nhớ các công thức và quy tắc cơ bản của việc tính đạo hàm. Sử dụng các phím chức năng trên máy tính cũng giúp cho quá trình tính toán nhanh chóng và chính xác hơn. Điều quan trọng là hiểu rõ ý nghĩa và ứng dụng của việc tính đạo hàm sin cos trong lĩnh vực toán học và các ngành khoa học khác. Qua bài viết này, hy vọng bạn đã có cái nhìn tổng quan về cách bấm máy tính đạo hàm sin cos và sẵn sàng áp dụng vào thực tế.