Công thức tính thể tích khối tứ diện: Tìm hiểu chi tiết về cách tính và ứng dụng

Công thức tính thể tích khối tứ diện là diện tích cơ sở nhân với chiều cao của khối. Khối tứ diện có thể có các hình đáy khác nhau như hình vuông, hình chữ nhật, tam giác, hay hình bất kỳ có diện tích cơ sở. Để tính thể tích của một khối tứ diện, bạn cần biết thông tin về các kích thước của hình đáy và chiều cao của khối.

1. Tứ diện là hình gì trong hình học?

Trong hình học, tứ diện là một loại hình chóp tam giác. Nó bao gồm 4 mặt là các tam giác, 6 cạnh thẳng và 4 góc đỉnh. Tứ diện có thể được xem như một hình chóp tam giác với đáy là một tam giác phẳng và các mặt tam giác nối với đáy bằng một điểm chung.

Có hai loại tứ diện phổ biến: tứ diện thông thường và tứ diện đều. Trong tứ diện thông thường, các mặt tam giác có thể có kích thước và hình dạng khác nhau. Trong khi đó, tứ diện đều có 6 cạnh và 4 mặt đều có cùng kích thước và hình dạng, tất cả các cạnh của tứ diện đều có cùng một độ dài.

Các tính chất của tứ diện:

• Tứ diện hay hình chóp tam giác phải có 4 cách chọn để chọn điểm đỉnh chóp.
• Tứ diện nội tiếp hình lập phương hoặc nội tiếp hình hộp sẽ có các cặp cạnh đối bằng nhau.
• Tứ diện gần đều nội tiếp với hình lập phương.

Công thức tính thể tích của khối tứ diện:

Để tính thể tích của một khối tứ diện, ta sử dụng công thức sau:

Thể tích = Diện tích cơ sở x Chiều cao

2. Công thức tính thể tích của khối tứ diện là gì?

Công thức để tính thể tích của một khối tứ diện là: Thể tích = Diện tích cơ sở x Chiều cao.

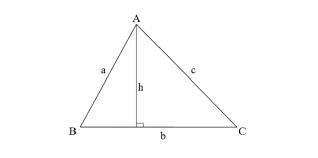
Với điểm chóp A và đáy ABCD, chiều cao của khối tứ diện được định nghĩa là khoảng cách từ điểm chóp A đến mặt phẳng đáy ABCD. Diện tích cơ sở có thể là hình vuông, hình chữ nhật, tam giác hoặc bất kỳ hình dạng nào có diện tích xác định.

Ví dụ:

Giả sử chúng ta có một khối tứ diện với đáy là một hình vuông và chiều cao là 5 cm. Độ dài cạnh của hình vuông đáy là 3 cm. Để tính thể tích của khối tứ diện này, chúng ta sử dụng công thức:

Thể tích = Diện tích cơ sở x Chiều cao

Thể tích = (Cạnh đáy x Cạnh đáy) x Chiều cao

Thể tích = (3 cm x 3 cm) x 5 cm

Thể tích = 45 cm³

3. Làm thế nào để tính thể tích của khối tứ diện có cạnh đáy là hình vuông?

Nếu khối tứ diện có cạnh đáy là hình vuông, ta có thể sử dụng công thức sau để tính thể tích:

Thể tích = Cạnh đáy x Cạnh đáy x Chiều cao.

Ví dụ:

Hãy giả sử chúng ta có một khối tứ diện với cạnh đáy là hình vuông và mỗi cạnh có chiều dài 4 cm. Chiều cao của khối tứ diện là 6 cm. Để tính thể tích của nó, chúng ta sử dụng công thức:

Thể tích = Cạnh đáy x Cạnh đáy x Chiều cao

Thể tích = 4 cm x 4 cm x 6 cm

Thể tích = 96 cm³

4. Khối tứ diện có thể có các hình đáy khác nhau không?

Có, khối tứ diện có thể có các hình đáy khác nhau. Đáy của một khối tứ diện có thể là một hình vuông, hình chữ nhật, tam giác hoặc bất kỳ hình dạng nào có diện tích xác định.

Công thức để tính thể tích vẫn được áp dụng cho tất cả các loại hình đáy, chỉ cần biết diện tích cơ sở và chiều cao của khối tứ diện.

Ví dụ:

Hãy giả sử chúng ta có một khối tứ diện với đáy là một hình chữ nhật và chiều cao là 8 cm. Chiều dài của hình chữ nhật là 6 cm và chiều rộng là 4 cm. Để tính thể tích của nó, chúng ta sử dụng công thức:

Thể tích = Chiều dài x Chiều rộng x Chiều cao

Thể tích = 6 cm x 4 cm x 8 cm

Thể tích = 192 cm³

5. Làm thế nào để tính thể tích của một khối tứ diện có hình đáy là hình chữ nhật?

Để tính thể tích của một khối tứ diện có hình đáy là hình chữ nhật, bạn cần biết chiều dài, chiều rộng của hình chữ nhật đáy và chiều cao của khối tứ diện. Công thức để tính thể tích sẽ là:

Thể tích = Chiều dài x Chiều rộng x Chiều cao.

Ví dụ:

Hãy giả sử chúng ta có một khối tứ diện với đáy là một hình chữ nhật và chiều cao là 10 cm. Chiều dài của hình chữ nhật đáy là 8 cm và chiều rộng là 5 cm. Để tính thể tích của nó, chúng ta sử dụng công thức:

Thể tích = Chiều dài x Chiều rộng x Chiều cao

Thể tích = 8 cm x 5 cm x 10 cm

Thể tích = 400 cm³

6. Tứ diện nội tiếp hình hộp và tứ diện gần đều được liên kết với những loại hình nào?

Tứ diện nội tiếp hình hộp và tứ diện gần đều có mối liên kết với các loại hình sau:

• Tứ diện gần đều có 3 cặp cạnh đối bằng nhau và nội tiếp với hình lập phương.
• Tứ diện nội tiếp hình hộp chữ nhật có 3 cặp cạnh đối bằng nhau và nội tiếp với hình hộp.

7. Có cần phải tính gián tiếp khi tính diện tích hoặc thể tích của một khối tứ diện không?

Có, trong một số trường hợp, chúng ta cần tính toán gián tiếp để tìm diện tích hoặc thể tích của một khối tứ diện. Điều này có thể xảy ra khi chúng ta không biết trực tiếp các giá trị như chiều dài, chiều rộng hoặc chiều cao của khối tứ diện.

Ví dụ:

Hãy giả sử chúng ta muốn tính thể tích của một khối tứ diện có hình đáy là một tam giác và chiều cao không được biết trực tiếp. Tuy nhiên, chúng ta biết rằng tứ diện này có thể được tạo thành từ việc cắt đi một phần của một hình chóp tam giác có cùng đáy và chiều cao với tứ diện ban đầu. Trong trường hợp này, chúng ta phải tính gián tiếp bằng cách tính toán diện tích tam giác đáy và chiều cao của nó.

8. Bạn có thể đưa ra ví dụ về việc áp dụng công thức tính thể tích khối tứ diện vào một bài toán cụ thể?

Ví dụ:

Giả sử chúng ta có một hộp nhỏ làm bằng gỗ với hình dạng tứ diện có đáy là một hình vuông. Kích thước của tứ diện này là 5 cm x 5 cm x 8 cm (chiều dài x chiều rộng x chiều cao). Để tính toán thể tích của hộp, chúng ta sử dụng công thức:

Thể tích = Cạnh đáy x Cạnh đáy x Chiều cao

Thể tích = 5 cm x 5 cm x 8 cm

Thể tích = 200 cm³

Vì vậy, thể tích của hộp là 200 cm³. Điều này có nghĩa rằng hộp có khả năng chứa được một lượng chất lỏng, ví dụ như nước, có thể không vượt quá 200 ml.

Tổng kết, công thức tính thể tích khối tứ diện là V = a^3, trong đó a là cạnh của khối tứ diện. Đây là một công thức đơn giản và dễ hiểu để tính toán thể tích của khối tứ diện. Việc áp dụng công thức này sẽ giúp chúng ta nhanh chóng và chính xác tính toán thể tích của khối tứ diện trong các bài toán liên quan.