Định luật Cu-lông là gì? Công thức Cu-lông và bài tập có lời giải chi tiết từ A -Z
Trong bài viết dưới đây, chúng tôi sẽ chia sẻ định nghĩa định luật Cu lông là gì? Công thức định luật Cu lông kèm theo các dạng bài tập thường gặp có lời giải chi tiết để các bạn cùng tham khảo nhé
Tham khảo thêm:
- Định luật Húc – Công thức tính lực đàn hồi của lò xo và bài tập từ A – Z
- Định luật bảo toàn động lượng là gì? Công thức và Ví dụ chứng minh
- Momen lực là gì? Công thức tính momen lực và bài tập có lời giải từ A- Z
Nội Dung
Định luật Cu-lông là gi?
Định luật Cu-lông: Lực hút hay đẩy giữa hai điện tích điểm đặt trong chân không có phương trùng với đường thẳng nối hai điện tích điểm đó, có độ lớn tỉ lệ thuận với tích độ lớn của hai điện tích và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.
Công thức:
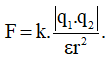
Trong đó:
- F: lực tương tác (F)
- k = 9.109: hệ số tỉ lệ (Nm2/C2)
- q1, q2: điện tích của 2 điện tích (C)
- r: khoảng cách giữa 2 điện tích (m)
Chú ý:
– Trong chân không ε = 1 hoặc không khí ε ≈ 1
– Các đơn vị thường gặp
1pC = 10-12C; 1nC = 10-9C; 1μC = 10-6C; 1mC = 10-3C
Cách giải bài tập liên quan đến định luật Cu- lông:
Tính lực tương tác, điện tích hay khoảng cách giữa 2 điện tích.
- Bước 1. Áp dụng định luật Cu-lông viết phương trình.
- Bước 2. Giải phương trình
- Bước 3. Kết luận.
Các dạng bài tập thường gặp của định luật Cu- lông
Bài tập 1: Hai điện tích q1 = -q; q2 = 4q đặt cách nhau một khoảng r. Nếu điện tích q1 tác dụng lực điện lên điện tích q2 có độ lớn là F thì lực tác dụng của điện tích q2 lên q1 có độ lớn là:
Giải:
Theo định luật Cu-lông ta có: Lực tác dụng của điện tích q1 lên q2 và lực tác dụng của điện tích q2 lên q1 bằng nhau:
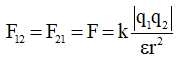
Bài tập 2: Lực tương tác tĩnh điện giữa hai điện tích điểm đứng yên đặt cách nhau một khoảng 4cm là F. Nếu để chúng cách nhau 1cm thì lực tương tác giữa chúng là:
Giải:
Khi r1 = 4cm : Lực tương tác tĩnh điện giữa hai điện tích:
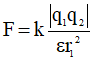
Khi r2 = 4cm : Lực tương tác tĩnh điện giữa hai điện tích:
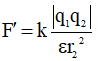
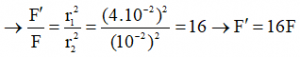
Bài tập 3: Khoảng cách giữa một prôton và một êlectron là r = 5.10-9 (cm), coi rằng prôton và êlectron là các điện tích điểm. Lực tương tác giữa chúng là:
Giải:
Áp dụng định luật Cu-lông:
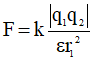
với q1 = +1,6.10-19 (C), q2 = -1,6.10-19 (C) và r = 5.10-9 (cm) = 5.10-11 (m)
⇒ F = 9,216.10-8 (N).
Mà 2 điện tích trái dấu nên lực tương tác là lực hút.
Bài tập 4: Hai điện tích điểm bằng nhau đặt trong chân không cách nhau một khoảng r = 2 (cm). Lực đẩy giữa chúng là F = 1,6.10-4 (N). Độ lớn của hai điện tích đó là:
Giải:
Áp dụng định luật Cu-lông:
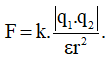
với q1 = q2 = q, r = 2 (cm) = 2.10-2 (m) và F = 1,6.10-4 (N)
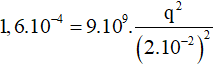
⇒ |q1| = |q2| = 2,67.10-9C
Bài tập 5: Hai điện tích điểm bằng nhau đặt trong chân không cách nhau một khoảng r1 = 2 (cm). Lực đẩy giữa chúng là F1 = 1,6.10-4 (N). Để lực tương tác giữa hai điện tích đó bằng F2 = 2,5.10-4 (N) thì khoảng cách giữa chúng là:
Giải:
Áp dụng định luật Cu-lông:
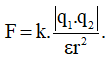
Ta có:
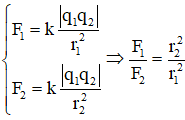
với F1 = 1,6.10-4 (N), F2 = 2,5.10-4 (N) , r1 = 2(cm)
⇒ r2 = 1,6 (cm).
Bài tập 6: Hai điện tích q1 và q2 đặt cách nhau 20 cm trong không khí, chúng đẩy nhau một lực F = 1,8 N. Biết q1 + q2 = -6.10-6 C và |q1| > |q2| . Điện tích q1 và q2 là:
Giải:
Hai điện tích đẩy nhau nên chúng cùng dấu, mặt khác tổng hai điện tích này là số âm
⇒ hai điện tích đều âm.
Ta có:
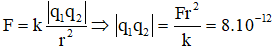
+ Kết hợp với q1 + q2 = -6.10-6C, ta có hệ phương trình
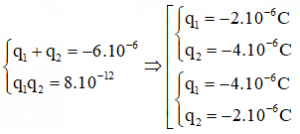
Vì
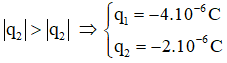
Bài tập 7: Tại hai điểm A và B cách nhau 20 cm trong không khí, đặt hai điện tích q1 = -3.10-6C, q2 = 8.10-6C. Biết AC = 12 cm, BC = 16 cm. Lực điện do hai điện tích này tác dụng lên q3 = 2.10-6 đặt tại C là:
Giải:
+ Các điện tích q1 và q2 tác dụng lên điện tích q3 các lực F13→ và F23→ có phương chiều như hình vẽ và độ lớn
![]()
+ Áp dụng quy tắc hình bình hành ta có lực tổng hợp tác dụng lên q3 có phương chiều như hình vẽ, và độ lớn
![]()
Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình