Căn bậc ba là gì? Cách tính căn bậc ba và các dạng bài tập có lời giải từ A – Z

Căn bậc ba là một trong những kiến thức không thực sự khó nắm bắt. Tuy nhiên, những dạng toán ứng dụng căn bậc a vào để giải quyết lại không hề đơn giản. Do đó, người dùng cần phải nắm chắc những kiến thức và tính chất quan trọng của căn bậc bba. Từ đó có thể vận dụng một cách hợp lý vào các bài toán. Tiếp tục cùng thptchuyenlamson.vn chinh phục căn bậc ba ở ngay bài viết dưới đây.

Tham khảo thêm:

• Lý thuyết và cách tính hàm số liên tục kèm theo VD có lời giải chi tiết nhất
• Lý thuyết và cách tính giới hạn của hàm số kèm bài tập có lời giải chính xác nhất
• Định nghĩa và hệ quả của định lý talet kèm bài tập có lời giải

Căn bậc ba là gì?

Căn bậc ba của một số thực a là số x sao cho x3 = a kí hiệu là 3√a .

Cho a ∈ R; 3√a = x ⇔ x3 = (∛a)3 = a

Mỗi số thực a đều có duy nhất một căn bậc ba

• Nếu a > 0 thì 3√a > 0
• Nếu a = 0 thì 3√a = 0
• Nếu a < 0 thì 3√a < 0

Tính chất của căn bậc ba

+ A < B ⇔ 3√A < 3√B

+ 3√A = 3√B ⇔ A = B

+ 3√AB = 3√A.3√B

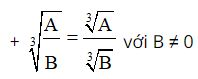
Các phép biến đổi của căn bậc ba

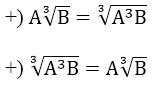
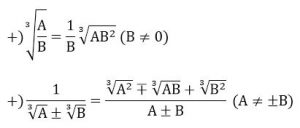
Các dạng bài tập thường gặp của căn bậc ba

Bài tập 1: So sánh:

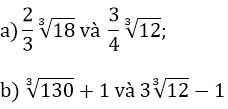
Lời giải:

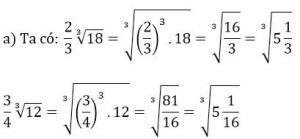
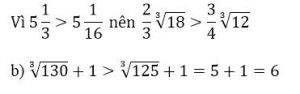
Bài tập 2: Tính:

Lời giải:

Để tính giá trị của A, ta tính A³ sau đó suy ra A

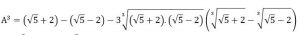
 ⇔ A³ = 4 – 3.A ⇔ A³ + 3A – 4 = 0

 ⇔ (A – 1)(A² + A + 4) = 0

 ⇔ A – 1 = 0 (vì A² + A + 4 > 0)

  ⇔ A = 1

  Vậy A = 1.

Bài tập 3: Giải phương trình sau:

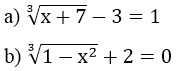
Lời giải:

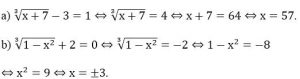
Bài tập 4: Cho biểu thức:

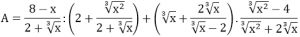
Với x ≠ ±8, x ≠ 0. Chứng minh rằng giá trị của A không phụ thuộc vào x.

Lời giải:

Đặt ³√x = y (y ≠ 0). Biểu thức A có dạng:

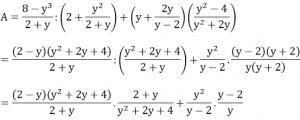
= 2 – y + y

= 2

Vậy với x ≠ ±8, x ≠ 0 thì A = 2, không phụ thuộc vào giá trị của x.

Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình