Phân thức đại số là gì? Tính chất và bài tập có đáp án cực hay

Phân thức đại số là gì ? Hai phân thức bằng nhau khi nào ? Dưới bài viết này của chúng tôi sẽ đem đến cho bạn những kiến thức vô cùng hữu ích xoay quanh chủ đề này. Hãy cùng chúng tôi theo dõi nhé !

Tham khảo thêm:

• Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp và bài tập có lời giải
• Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử và bài tâp có lời giải từ A- Z
• Phân tích đa thức thành nhân tử chung và bài tập có lời giải từ A- Z

Phân thức đại số là gì

Một phân thức đại số (hay nói gọn là phân thức) là một biểu thức có dạng A/B, trong đó A, B là những đa thức và B khác đa thức 0.

Trong đó:

• A được gọi là tử thức (hay gọi là tử).
• B được gọi là mẫu thức (hay gọi là mẫu).

Chú ý:

• Mỗi đa thức cúng được coi như một phân thức với mẫu thức bằng 1.
• Số 0, số 1 cũng là một phân thức đại số.

Hai phân thức bằng nhau

Hai phân thức A/B và C/D được gọi là bằng nhau nếu: A.D = B.C

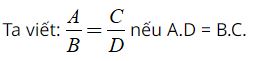
Tính chất cơ bản của phân thức đại số

Qui tắc đổi dấu

Đổi dấu cả tử và mẫu của một phân thức thì ta được phân thức mới bằng phân thức đã cho:

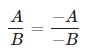
Ngoài ra, ta còn có một số quy tắc sau :

• Đổi dấu cả tử phần mẫu của phân thức: A/B = (-A)/(-B)
• Đổi dấu trước phân thức và dấu tử thức: A/B = -(-A)/B
• Đổi dấu trước phân thức và dấu của mẫu thức:  A/B = -(A)/(-B)

Các dạng bài tập phân thức đại số thường gặp

Dạng 1: Tìm điều kiện để phân thức xác định.

Phương pháp: Phân thức  A/B  xác định khi B≠0.

Vì dụ: Tìm điều kiện xác định của phân thức

a, Ta có:

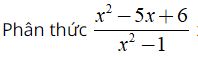
xác định ⇔ x² – 1 ≠ 0 ⇔ ( x – 1 )( x + 1 ) ≠ 0 ⇔ x ≠ ± 1.

Vậy điều kiện xác định của phân thức là x ≠ ± 1.

b, Ta có:

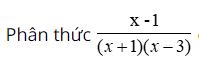
Để phân số có nghĩa thì (x + 1)(x – 3) ≠ 0 ⇔ x + 1 ≠ 0 và x – 3 ≠ 0

Vậy điều kiện xác đinh của phân thức là x ≠ -1 và x ≠ 3.

c, Ta có:

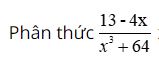
Để phân số có nghĩa thì x³ + 64 ≠ 0 ⇔ x³ ≠ -64 ⇔ x³ ≠ (-4)³ ⇔ x ≠ -4.

Vậy điều kiện xác định của phân số là x ≠ -4.

d, Ta có:

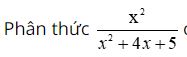
Để phân số có nghĩa thì x² + 4x + 5 ≠ 0 ⇔ x² + 4x + 4 + 1 ≠ 0

⇔ (x + 2)² + 1 ≠ 0 ⇔ (x + 2)² ≠ -1 (luôn đúng vì (x + 2)² ≥ 0 > -1 với mọi x)

Vậy biểu thức đã cho xác định với mọi x Î R.

Dạng 2: Tìm giá trị của biến số x để phân thức A/B nhận giá trị m cho trước.

Phương pháp:

• Bước 1: Tìm điều kiện để phân thức xác định: B ≠ 0
• Bước 2: Từ giả thiết ta có ( A/B)= m. Từ đó tìm được x
• Bước 3: So sánh với điều kiện ở bước 1 để kết luận.

Ví du 1: Chứng minh các phân thức sau bằng nhau

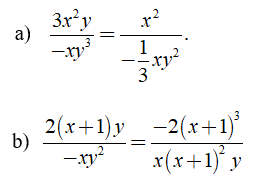
Lời giải:

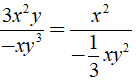
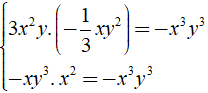
⇒ 3x²y.( – 1/3xy² ) = – xy³.x²

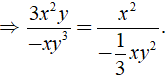
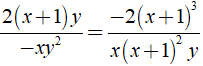
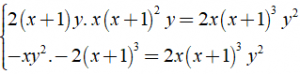
⇒ 2( x + 1 )y.x( x + 1 )²y = – xy². – 2( x + 1 )³

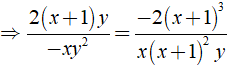
Ví dụ 2: Tìm đa thức thỏa mãn cho các phân số sau:

a, Ta có:

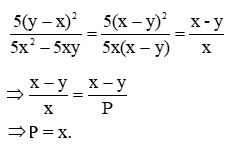
b, Ta có:

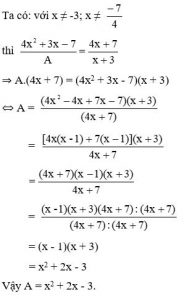
Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình