Con lắc đơn là gì? Công thức tính con lắc đơn và bài tập có lời giải chi tiết từ A -Z
Những câu hỏi về con lắc đơn luôn chiếm một tỉ lệ lớn trong các bài thi, luôn là một trở ngại lớn đối với học sinh khi bài tập về con lắc đơn yêu cầu phải hiểu rõ bản chất, hiện tượng và nắm chắc các kiến thức căn bản. Trong bài hôm nay, chúng ta sẽ đi sâu tìm hiểu về lý thuyết con lắc đơn và những dạng bài tập hay gặp.
Tham khảo thêm:
- Công thức tính áp suất và bài tập có lời giải chi tiết từ A – Z
- Lực hướng tâm là gì? Công thức tính lực hướng tâm và bài tập từ A – Z
- Công thức tính lực ma sát nghỉ và bài tập có lời giải chuẩn 100%
Nội Dung
Con lắc đơn là gì?
Con lắc đơn gồm một vật nhỏ khối lượng m, treo ở đầu một sợi dây không dãn, khối lượng không đáng kể, có chiều dài
Phương trình dao động:
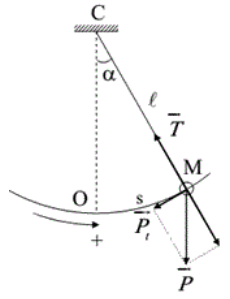
Xét một con lắc đơn: vật có khối lượng, sợi dây có chiều dài l, không dãn.
- Chọn trục tọa độ như hình vẽ, gốc tọa độ ở VTCB ( vị trí dây treo thẳng đứng). khi đó vị trí của vật được xác định bởi li độ cong (dài) s và li độ góc α. Với s = α.l
- Các lực tác dụng lên vật: trọng lực P, lực căng dây T→
- Theo Định luật II Niu-tơn ta có: P+ T = ma (1)
- Chiếu (1) lên phương chuyển động ta có:
- Psinα = ma
→ Dao động của con lắc đơn nói chung không dao động điều hòa
Xét: TH góc α nhỏ thì sinα ≈ α (rad) khi đó ta có pt:
![]()
Nghiệm của phương trình trên có dạng: s = S0cos(ωt + φ) hay: α = α0 cos(ωt + φ) (với S0 = α0l
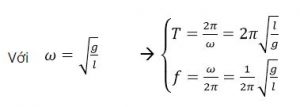
S0, α0,φ∶ được xác định từ điều kiện ban đầu của bài toán.
Năng lượng trong con lắc đơn:
Thế năng trọng trường của con lắc đơn:
Wt = mgh = mgl(1 – cosα)
Cơ năng của con lắc:
W = Wđ + Wt = Wtmax = mgl(1 – cosα0)
Động năng của con lắc đơn:
Wđ = W – Wt = mgl(cosα – cosα0) = (mv2)/2
![]()
Lực trong con lắc đơn:
Trong con lắc đơn: thành phần Psinα đóng vai trò là lực kéo về.
Chiếu (1) lên phương sợi dây ta có: 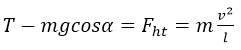 (do vật chuyển động tròn)
(do vật chuyển động tròn)
![]()
Các dạng bài tâp liên quan đến con lắc đơn
Câu 1. Tại một nơi có hai con lắc đơn đang dao động với các biên độ nhỏ. Trong cùng một khoảng thời gian, người ta thấy con lắc thứ nhất thực hiện được 4 dao động, con lắc thứ hai thực hiện được 5 dao động. Tổng chiều dài của hai con lắc là 164 cm. Chiều dài của mỗi con lắc lần lượt là
Giải:
Con lắc đơn có độ dài 1, trong khoảng thời gian Δt nó thực hiện được 4 dao động. Con lắc đơn có độ dài l2 = 1,6 – l1 cũng trong khoảng thời gian Δt như trước nó thực hiện được 5 dao động. Ta có biểu thức sau:
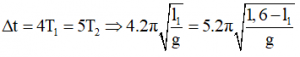
Giải phương trình ta được l1 = 1,00 m, và suy ra l2 = 0,64 m = 64 cm
Câu 2. Một đồng hồ quả lắc chạy đúng tại một nơi trên mặt đất. Người ta đưa đồng hồ từ mặt đất lên độ cao h = 5 km, bán kính Trái đất là R = 6400 km (coi nhiệt độ không đổi). Mỗi ngày đêm đồng hồ đó chạy
Giải:
Chu kỳ của con lắc khi ở mặt đất là
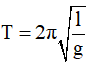
Khi con lắc ở độ cao h = 5 km thì chu kỳ dao động là
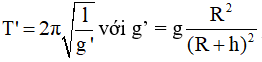 suy ra g’ < g → T’ > T → đồng hồ chạy chậm. Trong mỗi ngày đêm đồng hồ chạy chậm một lượng là Δt = 24.3600(T/T’ – 1), thay số ta được Δt = 68 s
suy ra g’ < g → T’ > T → đồng hồ chạy chậm. Trong mỗi ngày đêm đồng hồ chạy chậm một lượng là Δt = 24.3600(T/T’ – 1), thay số ta được Δt = 68 s
Câu 3. Một con lắc đơn có chu kỳ dao động T = 4s, thời gian để con lắc đi từ VTCB đến vị trí có li độ cực đại là:
Giải:
Thời gian con lắc đi từ VTCB đến vị trí có li độ cực đại là T/4.
Câu 4. Một con lắc đơn có chu kỳ dao động T = 3s, thời gian để con lắc đi từ VTCB đến vị trí có li độ x = A/2 là
Giải:
Chọn A. Vận dụng quan hệ giữa chuyển động tròn đều và dao động điều hoà, ta có thời gian vật chuyển động từ VTCB đến vị trí có li độ
x = A/2 là t = (π/6)/ω = T/12 = 0,250 s
Câu 5. Một con lắc đơn dao động với biên độ góc là 60° ở nơi có gia tốc trọng lực bằng 10 m/s2. Vận tốc của con lắc khi qua vị trí cân bằng là 4 m/s. Tính độ dài của dây treo con lắc.
Giải;
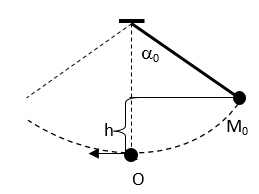
Dùng bảo toàn cơ năng (mv2)/2 = mgh
Với biên độ góc là 60° em vẽ hình sẽ thấy độ cao h = 1/2
Câu 6. Một con lắc đơn gồm quả cầu nhỏ khối lượng m treo vào sợi dây có chiều dài l = 40 cm. Bỏ qua sức cản không khí. Đưa con lắc lệch khỏi phương thẳng đứng góc α0 = 0,15 rad rồi thả nhẹ, quả cầu dao động điều hòa. Quãng đường cực đại mà quả cầu đi được trong khoảng thời gian 2T/3 là
Giải:
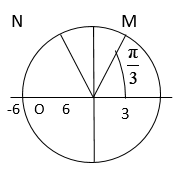
Ta có: s0 = l.α0 = 40.0,15 = 6 cm.
Quãng đường cực đại mà quả cầu đi được là khi vật qua vùng có tốc độ cực đại qua VTCB.
Coi vật dao động theo hàm cos. Ta lấy đối xứng qua trục Oy.
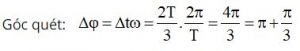
Trong góc quét: Δφ1 = π thì quãng đường lớn nhất vật đi được là: Smax1 = 2A = 12 cm.
Trong góc quét: Δφ1 = π/3 từ M đến N: thì Smax2 = 2.3 = 6 cm.
Vậy Smax = Smax1 + Smax2 = 18 cm
Câu 18. Một con lắc đơn gồm hòn bi nhỏ bằng kim loại được tích điện q > 0. Khi đặt con lắc vào trong điện trường đều có véc tơ cường độ điện trường nằm ngang thì tại vị trí cân bằng dây treo hợp với phương thẳng đứng một góc α với tanα = 3/4, lúc này con lắc dao động nhỏ với chu kỳ T1.
Nếu đổi chiều điện trường này sao cho véctơ cường độ diện trường có phương thẳng đứng hướng lên và cường độ không đổi thì chu kỳ dao động nhỏ của con lắc lúc này là:
Giải:
Ta có gia tốc do lực điện trường gây ra cho vật a = F/m = Eq/m (E là độ lớn cường độ điện trường).
Khi điện trường nằm ngang:
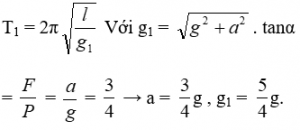
Khi điện trường hướng thẳng đứng lên trên
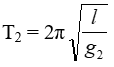
Với g2 = g – a = g – (3/4)g = (1/4) g
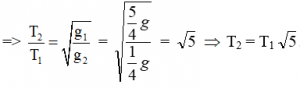
Mong rằng những nội dung trên đây sẽ giúp bạn trả lời được những thắc mắc câu hỏi của mình. Hơn hết đó là có thể giải được những bài toán của mình