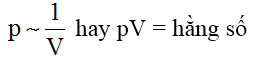Công thức tính cơ năng và bài tập có đáp án chuẩn 100%

Trong bài viết dưới đây, THPT CHUYÊN LAM SƠN chia sẻ khái niệm cơ năng là gì? Công thức tính cơ năng, định luật bảo toàn cơ năng và các dạng bài tập thường gặp có lời giải chi tiết từ A – Z để các bạn cùng tham khảo nhé

Nội Dung

Cơ năng là gì?

Cơ năng là tổng của động năng và thế năng. Nó là năng lượng kết hợp của chuyển động và vị trí của vật thể. Định luật bảo toàn cơ năng nói rõ, trong một hệ kín thì cơ năng không đổi.

Đơn vị của cơ năng là Jun (J)

Ví dụ: Một viên đá đặt trên một tấm kính, nó không có khả năng thực hiện công lên tấm kính. Nhưng nếu đưa nó lên độ cao h so với tấm kính thì khi rơi xuống nó có thể làm vỡ kính tức nó có khả năng sinh công. Vì vậy khi đưa viên đá lên độ cao h, viên đá đã có một cơ năng nào đó.

Công thức tính cơ năng

Cơ năng được tính bằng tổng động năng và thế năng của vật.

W = W_đ + W_t = ½mv² + mgz

Sự bảo toàn cơ năng của vật chuyển động trong trọng trường

Khi một vật chuyển động trọng trường chỉ chịu tác dụng của trọng lực thì cơ năng của vật là một đại lượng được bảo toàn.

W = W_đ + W_t = const hay ½mv² + mgz = const

Khi một vật chỉ chịu tác dụng của lực đàn hồi gây bởi sự biến dạng của một lò xo đàn hồi thì trong quá trình chuyển động của vật, cơ năng được tính bằng tổng động năng và thế năng đàn hồi của vật là một đại lượng bảo toàn

W = W_đ + W_t = const hay ½mv² + ½k.(Δl)²= const

Hệ quả:

Trong quá trình chuyển động của một vật trong trọng trường:

Nếu động năng giảm thì thế năng tăng và ngược lại.
Tại vị trí nào động năng cực đại thì thế năng cực tiểu và ngược lại.

Tham khảo thêm:

Định luật bảo toàn cơ năng

Trong khi chuyển động, nếu 1 vật chỉ chịu tác dụng của của trọng lực thì động năng hoàn toàn có thể chuyển thành thế năng và ngược lại và tổng của chúng tức là cơ năng sẽ được bảo toàn

Bài tập tính cơ năng thường gặp có lời giải

Ví dụ 1: Từ điểm M có độ cao so với mặt đất là 2m ném xuống một vật với vận tốc đầu 4m/s. Biết khối lượng của vật bằng 0,5kg, lấy g = 10m/s², mốc thế năng tại mặt đất. Khi đó cơ năng của vật bằng bao nhiêu?

Lời giải

Áp dụng công thức tính cơ năng ta có

W = W_đ + W_t = ½mv² + mgz = ½.0,5.4² + 0,5.10.2 = 14J

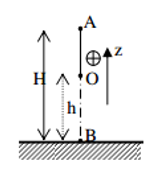
Ví dụ 2: Một vật được ném thẳng đứng lên cao với vận tốc là 20 m/s từ độ cao h so với mặt đất. Khi chạm đất vận tốc của vật là 30 m/s, bỏ qua sức cản không khí. Lấy g = 10 m/s². Hãy tính:

a. Độ cao h.

b. Độ cao cực đại mà vật đạt được so với mặt đất.

c. Vận tốc của vật khi động năng bằng 3 lần thế năng.

Lời giải

a. Chọn góc thế năng tại mặt đất (tại B).

Cơ năng tại O (tại vị trí ném vật):

W_O = ½mv₀² + mgz

Cơ năn tại B (tại mặt đất):

W_B = ½mv²

Theo định luật bảo toàn cơ năng: W (O) = W (B).

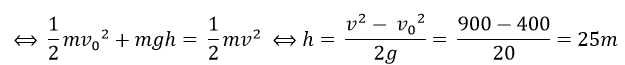
b. Độ cao cực đại mà vật đạt được so với mặt đất.

Gọi A là độ cao cực đai mà vật đạt tới.

Cơ năng tại A: W (A) = mgh.

Cơ năng tại B: W (B) = ½mv²

Theo định luật bảo toàn cơ năng: W (A) = W (B)

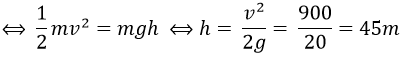
c. Gọi C là điểm mà W_đ(C) = 3W_t(C).

Cơ năng tại C:

W (C) = W_đ (C) + W_t (C)

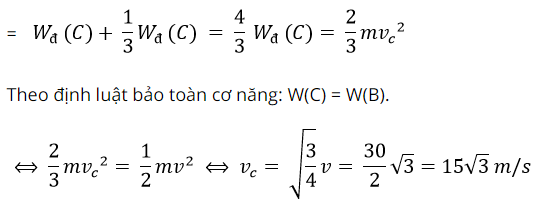
Ví dụ 3: Một vật được ném lên theo phương thẳng đứng từ một điểm A cách mặt đất một khoảng 4m. Người ta quan sát thấy vật rơi chạm đất với vận tốc có độ lớn bằng 12 m/s. Cho g=10m/s².

a) Xác định vận tốc của vật khi được ném. Tính độ cao cực đại mà vật có thể đạt được

b) Nếu vật được ném thẳng đứng xuống dưới vói vận tốc bằng 4m/s thì vận tốc của vật khi chạm đất bằng bao nhiêu?

Lời giải

chọn gốc thế năng tại mặt đất
a/ W_tmax = W_đmax ⇒ mgh_max= 0,5mv² ⇒ h_max= v²/2g = 12²/20 = 7,2m

Cơ năng tại vị trí ném = cơ năng tại vị trí vật đạt độ cao cực đại

mgh + 0,5mv_o² = mgh_max

⇒ 10 × 4 + 0,5v_o² = 10 × 7,2 ⇒ v_o = 8m/s
b/ Cơ năng tại vị trí ném = cơ năng tại mặt đất

mgh + 0,5mv_o² = 0,5mv² = 10 × 4 + 0,5 × 4² = 0,5v² => v = 4√6 (m/s)

Ví dụ 4: Một hòn bi có khối lượng 20 g được ném thẳng đứng lên cao với vận tốc 4m/s từ độ cao 1,6 m so với mặt đất.

a. Tính trong hệ quy chiếu mặt đất các giá trị động năng, thế năng và cơ năng của hòn bi tại lúc ném vật.

b. Tìm độ cao cực đại mà bi đạt được.

c. Tìm vị trí hòn bi có thế năng bằng động năng.

d. Nếu có lực cản 5N tác dụng thì độ cao cực đại mà vật lên được là bao nhiêu?

Lời giải

a. Chọn gốc thế năng tại mặt đất.

Động năng tại lúc ném vật:

W_đ = ½ mv² = 0,16 J.

Thế năng tại lúc ném vật:

W_t = mgh = 0,31 J.

Cơ năng của hòn bi tại lúc ném vật:

W = W_đ + W_t = 0,47 J.

b. Gọi điểm B là điểm mà hòn bi đạt được.

Áp dụng định luật bảo toàn cơ năng: W_A = W_B ⇔ h_max = 2,42 m.

c. 2 W_t = W ⇔ h = 1,175 m.

Ví dụ 5: Treo vật m = 1kg vào đầu một sợi dây rồi kéo vật khỏi vị trí cân bằng để dây treo hợp với phương thẳng đứng góc α_o. Xác định αo để khi buông tay, dây không bị đứt trong quá trình vật chuyển động. Biết dây chịu lực căng tối đa 16N; α_o ≤ 90^o.

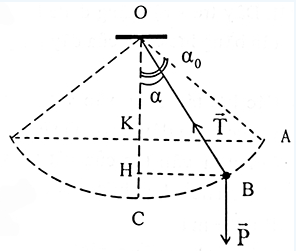
Lời giải

T – mgcosα = ma_ht = mv²/L ⇒ T = mgcosα + mv²/L

Đinh luật bảo toàn cơ năng

mgh_o = mgh + 0,5mv² ⇒ mgL(1-cosα_o) = mgL(1-cosα) + 0,5mv²

⇒ v² = 2gL(cosα – cosα_o)

⇒ T = mg(3cosα – 3cosα_o)

⇒ T_max = mg(3 – cosα_o)

Để dây không đứt thì T_max ≤ 16N ⇒ α_o ≤ 45^o

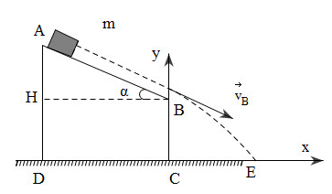
Ví dụ 6: Từ điểm A của một mặt bàn phẳng nghiêng, người ta thả một vật có khối lượng m = 0,2 kg trượt không ma sát với vận tốc ban đầu bằng 0 rơi xuống đất. Cho AB = 50 cm, BC = 100 cm, AD = 130 cm, g = 10 m/s² (hình vẽ). Bỏ qua lực cản không khí.

a. Tính vận tốc của vật tại điểm B và điểm chạm đất E.

b. Chứng minh rẳng quỹ đạo của vật là một parabol. Vật rơi cách chân bàn một đoạn CE là bao nhiêu?

c. Khi rơi xuống đất, vật ngập sâu vào đất 2cm. Tính lực cản trung bình của đất lên vật.

Lời giải

a. Vì bỏ qua ma sát nên cơ năng của vật được bảo toàn. Cơ năng của vật tại A là:

W_A = m.g.AD

Cơ năng của vật tại B: W_B = ½ m.v_b² + m.g.BC.

Vì cơ năng được bảo toàn nên: W_A = W_B

⇔ m.g.AD = ½ mv_B² + m.g.BC ⇔ v_B = √6 = 2,45 m/s.

Tương tự áp dụng định luật bảo toàn cơ năng tại A và E ta tính được:

v_E = 5,1 m/s.

b. Chọn hệ quy chiếu (hình vẽ). Khi vật rơi khỏi B, vận tốc ban đầu vB hợp với phương ngang một góc α. Xét tam giác ABH có:

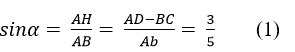
Phương trình chuyển động theo các trục x và y là:

x = v_B cosα.t (2)

y = h – v_B sinα.t – ½ gt² (3)

Từ (2) và (3) ta rút ra được:

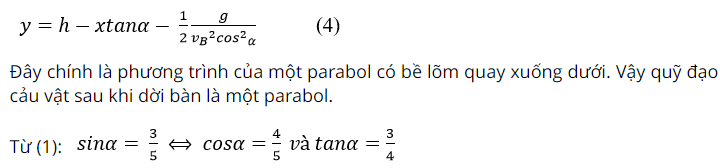
Khi vật chạm đất tại E thì y = 0. Thay giá trị của y và v_B vào phương trình (4), ta thu được phương trình:

13x² + 0,75x – 1 = 0 (5)

Giải phương trình (5) thu được x = 0,635 m. Vậy vật rơi cách chân bàn một đoạn CE = 0,635 m.

c. Sau khi ngập sâu vào đất 2 cm vật đứng yên. Độ giảm động năng gần đúng bằng công cản.

Gọi lực cản trung bình là F, ta có:

W_E – 0 = F.s ⇔ F = W_E/s = 130 N.

Bên trên chính là toàn bộ lý thuyết và công thức tính cơ năng mà THPT CHUYÊN LAM SƠN đã phân tích chi tiết có thể giúp các bạn hệ thống lại kiến thức đẻ vận dụng vào làm bài tập